20172303 2018-2019-1 《程序设计与数据结构》第1周学习总结

20172303 2018-2019-1 《程序设计与数据结构》第1周学习总结

教材学习内容总结

第1章 概述

1.软件工程

• 定义：一门关于高质量软件开发的技术和理论的学科。
• 目标：软件工程的目标与其他工程学科类似
  • 解决正确性问题————客户所需实现的需求
  • 按时且在预算之内给出解决方案————预算和给出方案的质量相匹配，学会折中
  • 给出高质量的解决方案————“高质量”由他人定义
  • 以合情合理的方式完成上面的事情————ACM职业道德规范(Code of Ethics and Professional Conduct)

2.软件质量的特征

• 在一定程度上讲，软件质量体系在旁观者的眼中，不同的身份对软件质量的要求存在差异。同时，一些软件质量特征之间有时是互斥的，不可能设计出一种软件符合所有的质量特征。
• 以每个学校都有的教务管理系统为例来具体阐述一下八个质量特征：
  • 正确性：一个教务管理系统要给用户提供选课、查分等功能，但绝对不可能有食堂点餐这个功能，因为它是一个有关教学相关事务的系统。而如果一个教务管理系统里不仅没有查分选课的功能，反而有各种各样的点餐功能、点外卖功能，那么这个教务管理系统的正确性很差。
  • 可靠性：在期末有很多同学会进入教务系统查分，如果当进入人数稍微多了一点系统就崩了，那么说明这个教务系统的可靠性很差。
  • 健壮性：假如出现了上一个特征中出现的情况，学校用了很久很久都没有修好，等同学们下个学期都快开学了才刚刚修好，那么这个系统的健壮性就很差。
  • 可用性：一个同学想要查询一下本学期的课表，结果在教务系统的网站内搜寻了几个小时最后在一个角落里找到了查询课表的入口，那么这个教务系统的可用性就很差。
  • 可维护性：过了几年之后有人发现了教务系统存在漏洞，于是有关人员决定对教务系统进行维护修复，但是之前开发这个系统的人都已经退休不干了，新来的程序员进行修复的时候发现当初写程序的人写的极烂无比乱七八糟根本找不到该修复的代码在哪儿，那么这个系统的可维护性就很差。
  • 可重用性：学校决定原来的教务系统太老了想重新做一个，但是从零开始过于费时间，就想着能否借用先前的老系统的相关组件来节省时间，但是发现之前的老系统做的太奇葩了而且太过时了真的没办法借鉴，那么原来这个老的教务系统的可重用性就很差。
  • 可移植性：假如一个教务系统用Windows可以打开并且很好的使用，结果有个同学用的MacBook根本打不开教务系统，只好含泪借其他同学的电脑上教务系统，那么这个教务系统的可移植性就很差。
  • 运行效率：一个同学上教务系统查分，结果查了一天一夜分都没有出来，那么这个系统的运行效率就很差。

3.数据结构

• 定义：计算机储存、组织数据的方式
• 上学期关于数据结构的相关学习内容
• 程序=数据结构+算法

第2章 算法分析

1.算法效率分析

• 算法效率通常用CPU的使用时间表示。
• 算法分析是计算机科学的基础。
• 算法的效率可以根据该问题的大小和处理步骤数来定义。

2.增长函数

• 定义：表示问题（n）大小与我们希望最优化的值之间的关系。该函数表示了算法的时间复杂度（CPU的使用时间）或空间复杂度（内存空间）
• 一般我们不需要知道某一算法确切的增长函数，而需要知道算法的渐进复杂度，又称为算法的阶次。
  • 渐进复杂度：基于增长函数中的主项，即表达式中增长最快的一项。
  • 阶次为增长函数提供了一个上界。除此之外，Ω表示函数的下界，Θ表示函数的上下界。
• 处理器速度的提高只会给增长函数增加常量。

3.大O记法

• 所有具有相同阶次的算法，从运行效率的角度来说都是等价的。
• 需要注意的是，大O记法只关注一个增长函数的主项，这句话看起来简单，但实际上有些时候很容易让人产生模糊概念，比如课上留的时间复杂度的计算题的第四个：

void fun (int n){
   int i=0;
   while(i*i*i<=n)
       i++;
}

• 有些同学通过将n带入不同常数计算后认为这段代码的时间复杂度是O(n的立方根+1)，就是混淆了阶次的概念，这段代码的增长函数是n的立方根+1，而它的时间复杂度则是O(n的立方根)。

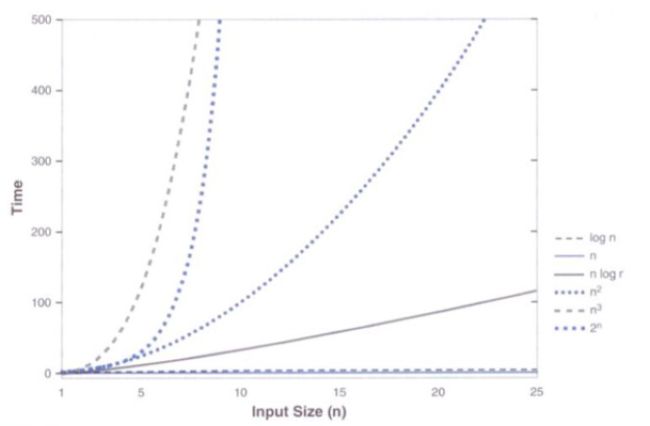
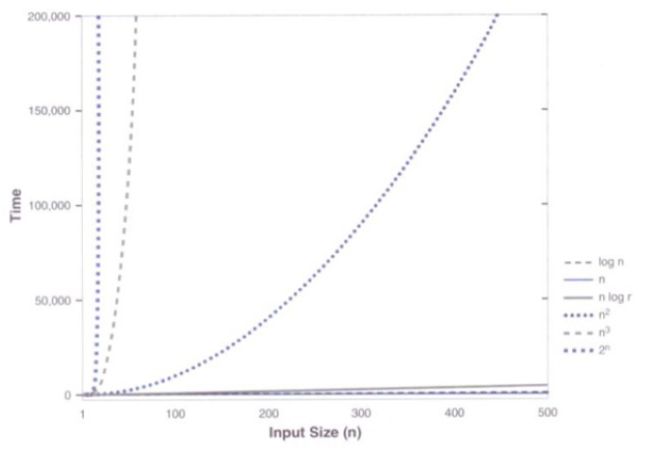
4.增长函数的比较

• 如果能保证问题（n）很小，那么使用何种算法是无关紧要的。
  
• 但是当问题（n）很大时，各种算法之间的差距就会很明显。
  

5.时间复杂度分析

• 步骤：首先确定循环体的阶n，然后乘以循环次数。
• 规则
  • 加法规则：T(n,m) = T1(n) + T2(n) = O (max ( f(n), g(m) )
  • 乘法规则：T(n,m) = T1(n) * T2(m) = O (f(n) * g(m))
  • 一个特例（问题规模为常量的时间复杂度）：在大O表示法里面有一个特例，如果T1(n) ＝ O(c)， c是一个与n无关的任意常数，T2(n) = O ( f(n) ) 则有T(n) = T1(n) * T2(n) = O ( c*f(n) ) = O( f(n) )
• 循环运行的复杂度分析

for(int count = 0; count < n; count++)
{
    //复杂度为O(1)的步骤系列
}
//复杂度为O(1×n)即O(n)

• 嵌套循环的复杂度分析

for(int count = 0; count < n; count++)
{
    for(int count2 = 0; count2 < n; count2++)
    {
        //复杂度为O(1)的步骤系列
    }
}
//复杂度为O(1×n×n)即O(n^2)

• 方法调用的复杂符分析

for(int count = 0; count < n; count++)
{
    printsum(count);
}

• 该代码段的复杂度要根据printsum方法的复杂度来确定，假如printsum方法为

public void printsum(int count)
{
    int sum = 0;
    for (int I = 1; I < count; I++)
        sum += I;
    System.out.println(sum);
}

• 那么上面的代码段的复杂度就为O(n^2)。而假如printsum方法为

public void printsum(int count)
{
    int sum = 0;
    sum = count * (count + 1)/2;
    System.out,println(sum);
}

• 那么代码段的复杂度为O(n)。

教材学习中的问题和解决过程

• 问题1：可靠性和健壮性都与软件的故障相关，那么它们之间的区别和联系究竟在哪儿？
• 问题1解决方案：书上的第九页有这么一段话：可靠性关注的是软件系统发生故障的频率以及在什么环境下发生故障，而健壮性关注的是软件系统出现故障时会发生什么。
• 我的理解是可靠性关注的是故障发生之前的相关内容，而健壮性关注的是故障发生之后的相关内容。

教材课后练习题

EX 2.1 下列增长函数的阶次是多少？

• a.10n^2+100n+1000
• 解答：阶次为O(n^2)
• b.10n^3-7
• 解答：阶次为O(n^3)
• c.2^n + 100n^3
• 解答：阶次为O(2^n)
• d.n^2×logn
• 解答：阶次为O(n^2×logn)

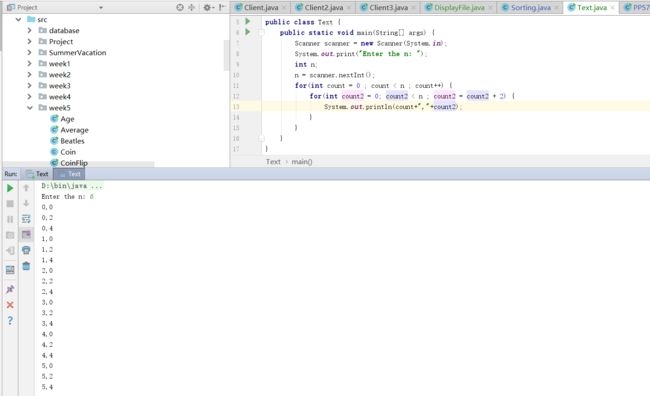
2.4 请确定下面代码段的增长函数和阶次

for(int count = 0 ; count < n ; count++)
    for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
        {
            System.out.println(count,count2);
        }
}

• 解答：增长函数为f(n)=n^2/2， 阶次为O(n^2)。

for(int count = 0 ; count < n ; count++)//循环次数为n，复杂度为O(n^2)
    for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)//循环次数为n/2，复杂度为O(n)
        {
            System.out.println(count,count2);//复杂度为O(1)
        }
}

• 为了确保正确性，我写了一个程序来实际测试了一下，发现的确内层的循环次数为n/2，外层的循环次数为n，证明增长函数和阶次是对的。
  

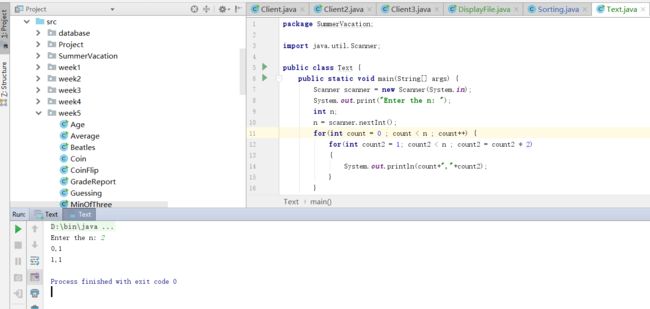
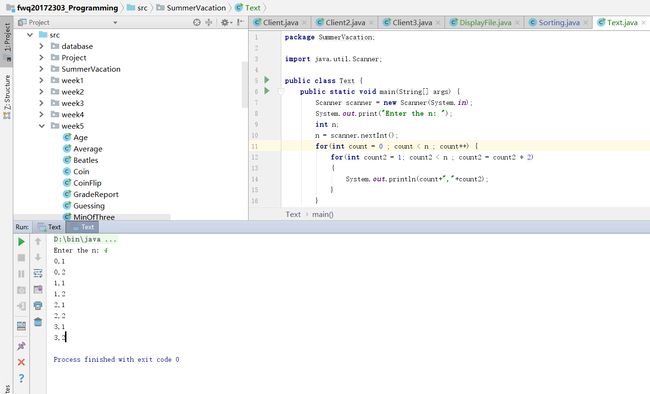
2.5 请确定下面代码段的增长函数和阶次

for(int count = 0 ; count < n ; count++)
    for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)
        {
            System.out.println(count,count2);
        }
}

• 解答：增长函数为f(n)=n×log2n，阶次为O(n×log2n)。

for(int count = 0 ; count < n ; count++)//循环次数为n，复杂度为O(n×log2n)
    for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)//循环次数为log2n，复杂度为O(log2n)
        {
            System.out.println(count,count2);//复杂度为O(1)
        }
}

• 再拿程序来测试一下：
  
  

结对及互评

• 本周结对学习情况
  • 20172322
  • 结对学习内容：本周内容相对简单，且时间比较紧迫，课本内容都是各自自行学习的。
    
• 博客中值得学习的或问题：
  • 优点：虽然很残忍.....但是感觉....没有优点....
  • 问题：内容有些过于简单，感觉很多东西都没有自己深入的理解。

其他（感悟、思考等，可选）

• 新的一个学期又开始了，很惭愧上个学期期末靠着背单词和写博客拿了一个不错的分数。本学期的学习目标是希望自己的动手能力能够有所加强，不会的东西要多去试一试，不要只局限于知识，一定要学会应用。
  

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	10/10	1/1	10/10

• 计划学习时间:5小时
• 实际学习时间:10小时
• 改进情况：本来感觉这周东西不多，老师还在课上都讲过了，没想到还是废了不少时间。本来尝试使用markdown语法去编辑公式，结果发现用不了，好像博客里给的方法只能在CSDN里面用o(╥﹏╥)o

参考资料

• 算法时间复杂度的计算
• markdown编辑数学公式

转载于:https://www.cnblogs.com/PFrame/p/9613948.html