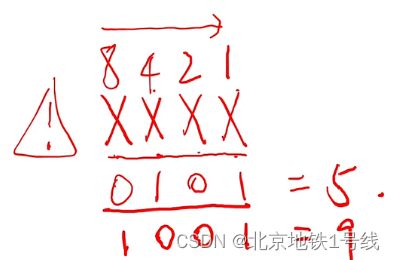2.数制与编码

目录

一. 进位计数制

（1）二进制，八进制，十进制，十六进制

（2）二进制，八进制，十六进制的转换

（3）十进制转换成任意进制

（4）真值和机器数

二. BCD码

（1）8421码

（2）余3码，2421码

三. 无符号整数的表示和运算

四. 带符号整数的表示和运算

（1）原码

（2）补码

（3）移码

五. 定点小数

---

数据如何在计算机中表示？运算器如何实现数据的算数、逻辑运算？

一. 进位计数制

（1）二进制，八进制，十进制，十六进制

十进制：0——9反应权重，所在的位置也反应权重：

基于乘法的计数方法（位权）：

推广到r进制：基数：每个数码位所用到的不同符号的个数，r进制的基数为r

• 二进制：0,1
• 八进制：0,1,2,3,4,5,6,7
• 十进制：0,1,2,3,4,5,6,7,8,9
• 十六进制：0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

为什么计算机采用二进制存储数据？

• ①可使用两个稳定状态的物理器件表示
• ②0，1正好对应逻辑值假、真。方便实现逻辑运算
• ③可很方便地使用逻辑门电路实现算术运算
   

（2）二进制，八进制，十六进制的转换

由于，所以八进制中一位对应二进制中的三位，16进制中的一位对应二进制中的四位。

注意：各种进制的常见书写方式：

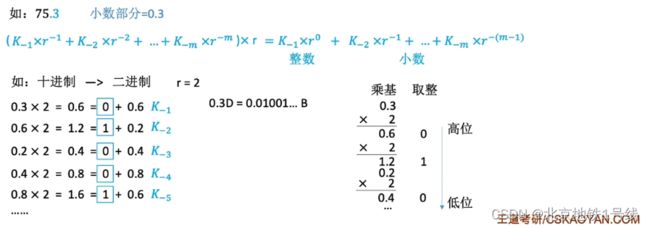
（3）十进制转换成任意进制

整数：除基取余法；小数：乘基取整法；

（4）真值和机器数

真值：符合人类习惯的数字
机器数：数字实际存到机器里的形式，正负号需要被“数字化”。

二. BCD码

BCD：Binary-Coded Decimal，用二进制编码的十进制。解决进制转换计算复杂的问题。

基本思想：用4个二进制位表示一位十进制。

（1）8421码

加法运算的修正：如果两位BCD码相加结果落在1010——10010（10-18）范围内，要进行+6修正，这是因为用4个二进制位表示一位十进制有6个冗余。

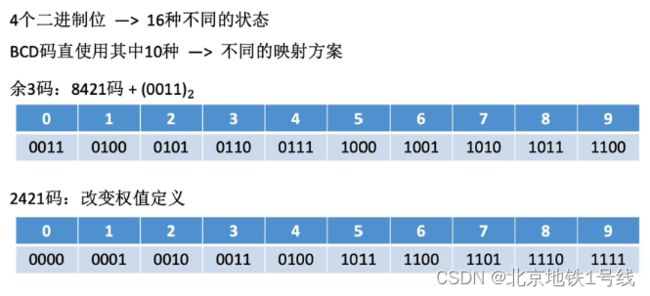
（2）余3码，2421码

在2421码中，为了避免歧义，5——9的所有首位数字必须是1.

显然，余3码是无权码（因为各位的权值不确定），8421码和2421码都是有权码。

三. 无符号整数的表示和运算

无符号整数，即自然数：0，1，2，3...C语言中通常定义如下：

unsigned short a=1;
unsigned int b=2;

计算机硬件能支持的无符号整数位数有上限，由机器字长决定。

1. 全部二进制位都是数值位，没有符号位，第i位的位权是；
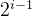2. n bit无符号整数表示范围0~，超出则溢出只保留低位，意味着该计算机无法一次处理这么多；
3. 可以表示的最小的数全0，可以表示的最大的数全1；
    

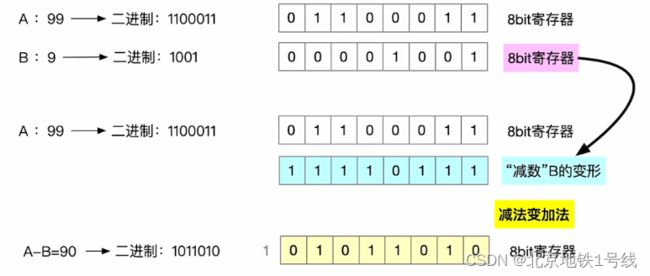
计算机硬件如何做无符号整数的加法：从最低位开始，按位相加，并往更高位进位。

计算机硬件如何做无符号整数的减法：“被减数”不变，“减数”全部位按位取反、末位+1，减法变加法。然后从最低位开始，按位相加，并往更高位进位。

四. 带符号整数的表示和运算

无符号整数，即整数：-2，-1，1，2，3...C语言中通常定义如下：

short a=-1;
int b=2;

（1）原码

• ①符号位“0/1”对应“正/负”，剩余的数值位表示真值的绝对值；
• ②若机器字长n+1位，带符号整数的原码表示范围：；
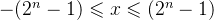• ③真值0有两种形式：+0和-0 ，[+0]原=0,0000000;[-0]原=1,0000000；
   

常见书面写法：x=-19，[x]原=1,0010011。若未指明机器字长，也可写为：[x]原=1,10011

原码的缺点：符号位不能参与运算，需要设计复杂的硬件电路才能处理。

（2）补码

计算机硬件如何做补码的加法：从最低位开始，按位相加(符号位参与运算)，并往更高位进位。

补码的减法运算：

接下来：对于给定的数，如何求相反数的补码表示？

计算机硬件如何做带符号数补码的减法：“被减数”不变，“减数”全部位按位取反、末位+1，减法变加法。然后从最低位开始，按位相加，并往更高位进位。
 

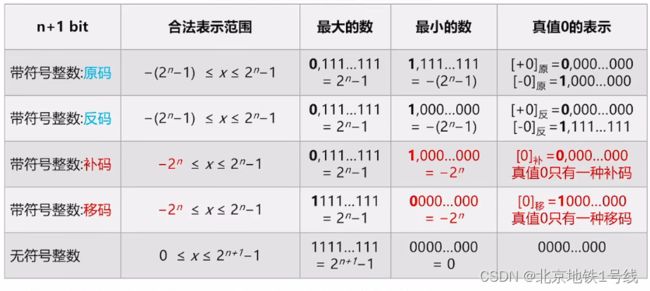
Tips：计算机内部，所有带符号整数的加、减法都要先转化为补码。原码和反码的合法表示范围完全相同，都有两种方法表示真值0。补码的合法表示范围比原码多一个负数，只有一种方法表示真值0。

常见考点：两个数A和B进行某种运算后，是否发生溢出?——手算做题可以带入十进制验证，是否超出合法范围。

（3）移码

移码：补码的基础上将符号位取反。注意：移码只能用于表示整数。

显然，移码能表示的整数范围与补码相同。

五. 定点小数

定点小数的原码，反码，补码转换和定点整数完全一样（没有移码）。

定点小数的加法，减法计算也同前。