机器学习中的假设检验
- 正态性检验
- 相关分析
- 回归分析
所谓假设检验,其实就是根据原假设来构造一种已知分布的统计量来计算概率,根据概率值大小来判断能否拒绝原假设,从而得到一种结论。假设检验的过程就是,构造一个原假设成立条件下的事件A,计算该A发生的概率P是否低于显著水平,即A是否为小概率事件(P值小于显著水平),若A为小概率事件,则原假设的发生的概率也不会很大,即可以拒绝原假设;而当p值大于显著水平,只是说明证伪结果不能推翻原假设即不能拒绝原假设而已,并不能说明原假设就是正确的就可以接受原假设。
例如机器学习中的最基本假设:样本分布与总体分布相似,样本可以代表总体,反之若样本不能反映总体,也就没有做机器学习的必要了,所以在训练模型之前,需要做一些假设检验,来决定能否使用该模型。
导入数据
import seaborn as sea
# 如遇中文显示问题可加入以下代码
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
import copy
#导入数据
data_raw=pd.read_excel(r'方差分析.xlsx')
data_clean=copy.deepcopy(data_raw)
data_clean.head(5)正态性检验:数值特征的正态分布检验(一组数据的正态性检验)
- 可视化:直方图、qq图,pp图,计算偏度与峰度
- S-W检验:小样本≤50
- K-S检验:大样本>50
Q-Q图是基于分位数的,P-P图是基于累积分布的
偏度:数据对称程度,
- skewness = 0 —— 分布形态与正态分布偏度相同
- skewness > 0 —— 正偏差数值较大,为正偏或右偏。长尾巴拖在右边,数据右端有较多的极端值
- skewness < 0 —— 负偏差数值较大,为负偏或左偏。长尾巴拖在左边,数据左端有较多的极端值
峰度:数据陡峭程度
- kurtosis = 0 —— 与正态分布的陡缓程度相同
- kurtosis > 0 —— 比正态分布的高峰更加陡峭——尖顶峰
- kurtosis < 0 —— 比正态分布的高峰来得平台——平顶峰
S-W、K-S检验:
原假设:服从正态分布
def checkNormal(df,tiger):#df:dataframe、数值
import seaborn as sea
from scipy import stats
plt.figure(figsize=(8,5))
#绘制直方图
plt.subplot(131)
sea.histplot(data=df,x=tiger, bins='auto', kde=True)
#绘制散点图
plt.subplot(132)
sea.scatterplot(data=df,x=df.index, y=tiger)
#绘制qq图
plt.subplot(133)
stats.probplot(df[tiger], dist='norm', plot=plt)
name=['偏度','峰度','S-W(≤5000):p','K-S(>5000):p']
value=[data_clean[tiger].skew(),
data_clean[tiger].kurt(),
stats.shapiro(data_clean[tiger])[1],
stats.kstest(data_clean[tiger], 'norm',args=(data_clean[tiger].mean(),data_clean[tiger].std()))[1]
]
result=pd.DataFrame({'name':name,'value':value})
print(result)
# #计算偏度,峰度
# print('偏度:',data_clean[tiger].skew())
# print('峰度:',data_clean[tiger].kurt())
# #s-w检验
# stats.shapiro(data_clean[tiger])[1]
# #k-s检验
# stats.kstest(data_clean[tiger], 'norm',args=(data_clean[tiger].mean(),data_clean[tiger].std()))[1]#检验方法,例如'norm','expon','rayleigh','gamma',这里我们设置为'norm',即正态性检验
check(data_clean,'被投诉次数')首选方法是图示法,即利用直方图、Q-Q、PP图进行观察,如果分布严重偏态(左偏/右偏)和尖峰分布则建议进行假设检验。在样本量较小的时候优先选择S-W检验,反之使用K-S检验。统计学上正态性检验:原假设服从正态分布,即一般P值大于0.05我们可认为该组数据是符合正态分布。
相关分析
- 数值变量与数值变量:相关系数显著性检验
T检验:原假设:线性不相关(相关系数=0)- 分类变量与数值变量:方差分析:分类变量对数值变量是否有显著影响
F检验:原假设:分类变量对数值变量没有影响,当分类变量只有两个类别时,也可用T检验。- 分类变量与分类变量:卡方分析:验证分类变量之间是否独立
卡方检验:原假设:两个分类变量相互独立T检验与方差分析均为差异显著性检验,用于比较两个(T检验)或者多个样本(方差分析)的差异是否显著的统计分析方法,原假设:H0:两组均值或多组均值相等。
T检验:
- 均值差检验,检验两组数据(总体均为正态,且方差齐)的均值是否相等且数据为定量数据(分类变量对应数值变量)。
- 此外,T检验也可以对相关系数、回归系数做显著性检验,原假设:H0:相关系数=0,H0:回归系数β=θ
方差分析:原假设H0:各个类别下的总体均值均相等,检验多个总体(方差齐)均值是否相等的方法,虽然它形式上是比较总体均值,但是本质上是研究变量之间的关系。这里的变量中,自变量是分类型的,因变量是数值型的,所研究的关系是是指分类自变量对数值因变量的影响。当分类特征只有两个类别时,此时方差分析(F检验)等价于T检验。
卡方分析:是一种非参数检验(对总体分布没有假定)
- 可以用于独立性检验:可用于检验2个分类变量之间是否独立来判断是否相关,
原假设H0:两个分类变量相互独立- 也可用于总体分布假设的检验(拟合优度检验)
原假设:假设数据服从某种分布,从而根据概率密度函数得到概率值,计算观测频数与理论频数(np)的偏离程度,得到卡方统计量,来判断是否落在拒绝域内
导入数据
#加载数据
data_raw=pd.read_excel(r'./Data/泰坦尼克号/titanic3.xls')
data_clean=copy.deepcopy(data_raw)
#查看数据
data_clean.info()相关系数显著性检验
#method{‘pearson’, ‘kendall’, ‘spearman’} :用来计算相关性的方法,默认为皮尔森相关系数
#min_periodsint:可选参数,为了获得有效结果所需要的最小的样本数量
def getCorr(inx,method='pearson'):#method:'pearson', 'spearman', 'kendall'
#输出相关系数和显著性检验P值
inx_num=inx.select_dtypes('number')
cols=inx_num.columns
m,n=len(cols),len(cols)
# print(cols)
data_corr=pd.DataFrame(data=np.zeros((m,n)),index=cols,columns=cols)
data_corr_p=pd.DataFrame(data=np.zeros((m,n)),index=cols,columns=cols)
for i in data_corr.index:
for j in data_corr.columns:
if method=='pearson':
corr_p=scipy.stats.pearsonr(inx_num[i], inx_num[j])
elif method=='spearman':
corr_p=scipy.stats.spearmanr(inx_num[i], inx_num[j])
elif method=='kendall':
corr_p=scipy.stats.kendalltau(inx_num[i], inx_num[j])
data_corr.loc[i,j]=corr_p[0]
data_corr_p.loc[i,j]=corr_p[1]
return data_corr,data_corr_p
corr,corr_p=getCorr(data_clean)方差分析
方差分析检验多个类别对应的总体均值是否相等的方法,是一种参数检验,对数据分布有一定要求。数据用什么样的检验方法进行分析,实际上取决于我们构造的统计量服从什么样的分布,只有服从这个分布,才可以利用这个分布的相关函数计算P值,如果实际上不服从这个分布,那么计算出的P值自然是不准确的。
- 正态性:每个类别对应的数据服从正态分布
原假设:服从正态分布 - 方差齐:每个类别对应的总体的方差相同(每个分类特征对应的数值变量的方差相同)
原假设:每个类别对应的方差相同
方差分析:理论上要求满足正态性和方差齐才可以使用方差分析,当数据不满足正态性和方差齐性假定时,参数检验可能会给出错误的答案。若正态性或方差齐不满足,则使用非参数检验方法检验分类特征对数值特征是否有显著影响,非参数检验对数据分布不作假设。
方差分析流程:
如下图所示,
正态性检验:原假设:行业中每个类别对应的总体分布为正态分布
方差齐检验:原假设:行业中每个类别对应的总体方差相同
方差齐检验前提:每个类别对应的总体均服从(近似)正态分布,每个类别的样本相互独立
每个类别对应的数据的正态性检验
#正态性检验:每个类别对应数据的正态分布检验
def checkGroupNormal(df,tiger,cat):#df:dataframe,tiger:数值变量,cat;分类变量
import seaborn as sea
from scipy import stats
group=df[[cat,tiger]].groupby(cat)
means=group.mean()
stds=group.std()
n=len(means)
#绘制每个分类对应数据的直方图
# plt.figure(1)
# for i in range(1,n+1):
# plt.subplot(n,1,i)
# sea.histplot(data=df[df[cat]==means.index[i-1]],x=tiger, bins='auto', kde=True,label=means.index[i-1])
# plt.legend()
#绘制散点图
# plt.figure(2)
# for i in range(1,n+1):
# plt.subplot(n,1,i)
# sea.scatterplot(data=df[df[cat]==means.index[i-1]],x=df[df[cat]==means.index[i-1]].index, y=tiger,label=means.index[i-1])
# plt.legend()
#绘制qq图
# plt.figure(3)
# for i in range(1,n+1):
# plt.subplot(n,1,i)
# stats.probplot(df[df[cat]==means.index[i-1]][tiger], dist='norm', plot=plt)
#计算偏度,峰度,s-w检验,k-s检验
value=[]
for i in means.index:
data=data_clean[[cat,tiger]][data_clean[cat]==i][tiger]
#偏度
a=data.skew()
#峰度
b=data.kurt()
#s-w检验
c=stats.shapiro(data_clean[tiger])[1]
#k-s检验
u,std=means.loc[i,tiger], stds.loc[i,tiger]
d=stats.kstest(data, 'norm',(u,std))[1]
value.append([a,b,c,d])
name=['偏度','峰度','S-W(≤5000):p','K-S(>5000):p']
result=pd.DataFrame(data=np.array(value),index=means.index,columns=name)
return result
print(checkGroupNormal(data_clean,'被投诉次数','行业'))方差分析按照分类变量个数不同,可以分为单因素方差分析、双因素方差分析以及多因素方差分析。
- 单因素方差分析
单因素效应:其他因素水平固定时,某一因素不同水平之间的变化(其他分类特征水平类别时,某一分类特征不同类别之间的变化)。 - 双因素方差分析
主效应:不考虑其他因素的影响下,某因素不同水平之间的平均变化
交互效应:两因素间的交互作用引起的其单独效应的平均变化 - 多因素方差分析
注意:双因素分析或者多因素分析,均需要对每个分类特征的每个类别对应的数据做正态性检验和方差齐检验,均符合要求时才可以做方差分析,否则要使用非参数检验。
方差齐检验
def equalVarCheck(inx,tiger,categoric=[]):#tiger:数值变量,categoric:分类变量
inx_tiger=inx[tiger]
inx_class=list(inx.select_dtypes(exclude='number').columns) if len(categoric)<1 else categoric
for col in inx_class:
data=inx[[col,tiger]]
group=data.groupby(col)#分组
group_list=[list(np.array(i[1])[:,-1]) for i in group]#嵌套列表
_,p=stats.levene(*group_list)
print(col,p)
equalVarCheck(data_clean,'被投诉次数',['行业','地区'])当数据满足正态性和方差齐时,
单因素方差分析:
from statsmodels.stats.anova import anova_lm #方差分析
from statsmodels.formula.api import ols # 最小二乘法拟合
#单因素方差分析
model = ols('被投诉次数~C(行业)',data=data_clean).fit()
model_a=anova_lm(model)
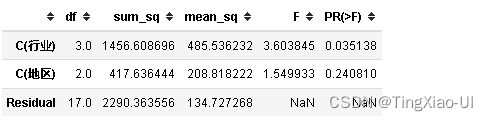
model_a
# 组间平方和
# SSE=1456
#组内平方和
# SSA=2708
#R_2=SSE/(SSE+SSA)计算关系强度R²
R_2=model_a['sum_sq'][0]/model_a['sum_sq'].sum()
R_2以上单因素方差分析可以得出,行业因素对投诉次数有显著影响,行业因素有四种类别,四组之间的投诉次数有显著差异,但是我们不知道哪种行业与其他行业的不同,多重比较可以解决这个问题。
#
单因素各个水平之间的显著差异(多重比较):各组均值差异的成对检验
在检验出行业因素对投诉次数有显著影响,还需判断行业因素具体是哪两个类别对应的总体均值不相等,即行业因素中具体是哪两种行业才有显著差异。注意与方差齐检验的区别:方差齐是每个类别对应的总体方差相同。
# 这个看某个因素各个水平之间的差异
from statsmodels.stats.multicomp import pairwise_tukeyhsd
# 行业与被投诉次数的影响 显著水平为0.05
print(pairwise_tukeyhsd(data_clean['被投诉次数'], data_clean['行业'], alpha=0.05)) # 第一个必须是被投诉次数, 也就是我们的指标- pairwise_tukeyhsd函数默认原假设H0:各个水平两两组合没有差异,若P>0.05,接受原假设,反之拒绝原假设
- Falset:说明无显著差异,True:有显著差异
- 这个可以得到的结论是在显著水平0.05的时候, 航空公司和零售业的p值小于0.05, reject=True, 即认为航空公司和零售业之间有显著性差异(均值明显不同)。
# 地区与被投诉次数的影响
print(pairwise_tukeyhsd(data_clean['被投诉次数'], data_clean['地区'], alpha=0.05)) #地区变量对投诉次数没有显著影响,其各个水平之间也没有显著差异。
在机器学习中特征选择中,若投诉次数为目标变量,行业和地区为分类特征,则根据单因素方差分析结果,可过滤地区特征;对行业特征做one-hot编码后,可只保留行业-航空公司、行业-零售业这两种特征,或者对行业特征做one-hot编码后,做数值变量之间的相关性分析
双因素方差分析
- 无交互作用:"加法"组合,即类似于特征工程中特征的线性组合
- 有交互作用:“乘法”组合,即类似于特征工程中特征的多项式组合(非线性)
无交互作用
model = ols('被投诉次数~C(行业)+C(地区)',data=data_clean).fit()
model_a_b=anova_lm(model)
model_a_b有交互作用
model = ols('被投诉次数~C(行业)*C(地区)',data=data_clean).fit()
model_ab=anova_lm(model)
model_ab从结果可以看出,依然是行业特征对目标(被投诉次数)有显著影响,地区以及行业和地区的交互作用没有显著影响。
可视化观察
fig = interaction_plot(data_clean['行业'],data_clean['地区'], data_clean['被投诉次数'],ylabel='被投诉次数', xlabel='行业')从图中也可以看出
- 每个地区在每个行业的走势上一致,即地区与行业的交互作用不明显;
- 航空公司和零售业对应的被投诉次数差异明显
. ols函数里面公式的写法
- '被投诉次数~C(行业)+C(地区)+C(行业):C(地区)' :相当于被投诉次数是y(指标), 行业和地区是x(影响因素), 三项加和的前两项表示两个主效应, 第三项表示考虑两者的交互效应, 不加C也可。
- '被投诉次数~C(行业, Sum)*C(地区, Sum)'和上面效果是一致的, 星号在这里表示既考虑主效应也考虑交互效应,'被投诉次数~C(行业)+C(地区)':这个表示不考虑交互相应
多因素方差分析:
多因素方差分析和双因素方差分析原理上一致
- 无交互作用
model = ols(''被投诉次数~C(行业)+C(地区)+C(其他)' ,data=data_clean).fit()
model_a_b=anova_lm(model) - 有交互作用
model = ols(''被投诉次数~C(行业)*C(地区)*C(其他)' ,data=data_clean).fit()
model_ab=anova_lm(model)
非参数检验:分类变量与数值变量关系
当数据的正态性或方差齐不满足时,需改用非参数检验(非参数检验利用的是数据间的次序关系,会造成了一定的信息损失)。Welch’s ANOVA就是其中一种非参数检验方法。在python中使用Welch’s ANOVA需要安装pingouin库。其中的welch_anova和pairwise_gameshowell分别用于Welch’s ANOVA和两两比较。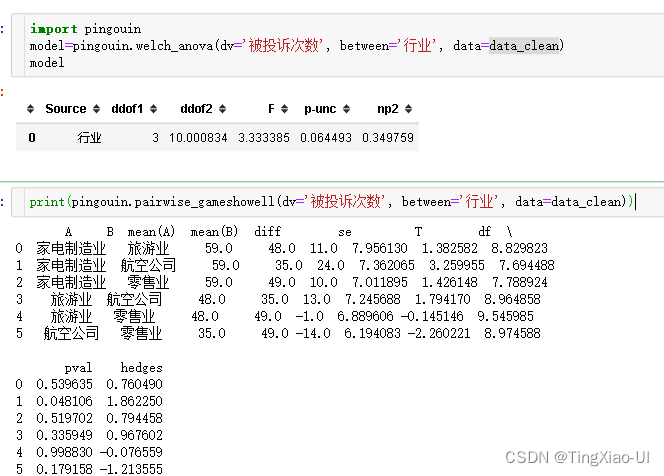
卡方分析
分类变量间的独立性检验,原假设:两个分类变量相互独立
from scipy.stats import chi2_contingency检验地区与行业两个分类变量是否独立,生成地区与行业的频数交叉连接表
df=pd.crosstab(data_clean['地区'], data_clean['行业'])#交叉连接表:频数
dfX_2, p, dof, expected = chi2_contingency(df,correction=False)
#dof:degree of freedom,(3-1)(4-1)
#p:概率值
## 卡方值、P值、自由度、理论(期望)频数,无需耶茨连续性修正
#当某个单元格的频数(np)小于5时,需要进行校正correction=False不能拒绝原假设,不能拒绝地区和行业分类变量相互独立。
回归方程显著性检验、回归系数显著性检验
为什么要对回归方程和回归系数做显著性检验?
许多数据统计分析结果来自于部分甚至少量的样本,因此所得的统计结果可能存在偶然性,需要对样本统计结果进行显著性检验,以查看统计结果的可靠性程度。
- 回归方程的显著性检验:F,原假设:各个回归系数均为0
检验回归方程是判断自变量和因变量之间是否显著的线性关系 - 回归系数的显著性检验:T,原假设:某个回归系数=0
检验回归系数时判断自变量(特征)对因变量(目标)是否有显著影响 - 逻辑回归方程、回归系数显著性检验:卡方检验
import statsmodels.api as sm
#最小二乘法拟合
result=sm.OLS(Y,X).fit()
result.summary()
#拟合度:
#R2=0.959:R2接近1,拟合程度好
#Adj.R-squared:修正R2
#回归方程的显著性检验:F,原假设:各个回归系数=0
#F-statistic:F值=891.3
#Prob:回归方程的P值=0.,小概率事件,原假设不成立
#回归系数的显著性检验:T,原假设:某个回归系数=0
# P>|t|:t》|t_a/2|,P越小于a,原假设越是小概率事件,越拒绝原假设,即某个回归系数对应的特征对标签Y是显著的
#置信区间有什么用呢?图中P>|t|表示双侧T检验
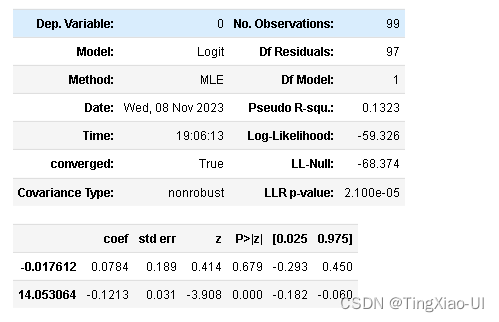
model = sm.Logit(y, x)
result = model.fit()
result.summary()对回归方程和回归系数做显著性检验,可以帮助我们做模型诊断。
回归分析,通常需要满足一些基本假设
- 自变量和因变量之间存在线性关系
- 样本之间是独立的,即样本的观测值不受其他样本的影响
- 自变量之间不存在高度相关性,即不出现多重共线性问题
某个变量的回归系数不显著可能的原因:
- 特征与目标存在非线性关系,未提取出来,因为线性模型只能捕捉到线性关系,而不能处理非线性关系。
解决办法:① 增加新的非线性特征。② 变换自变量和因变量。取对数、开方、平方根等,以达到线性关系。③ 使用非线性回归模型,例如多项式回归、指数回归等
- 存在共线特征导致伪回归,变量之间存在强相关性,会导致回归分析结果不稳定,使得回归系数不显著。
解决办法:① 删除相关性较高的自变量,② 合并相关性较高的自变量,即将相关性高的变量组合成一个新的变量,③ 使用PCA,将原始的高度相关的自变量转换成一组线性无关的主成分,④ 正则化方法(如岭回归、Lasso回归)或者自变量选择方法(逐步回归,最小角回归)来缩减回归系数,减小多重共线性影响
回归不显著也可能是由于未引入自变量之间存在交互作用导致的。 在回归分析中,交互作用指的是自变量之间相互影响的情况。 当存在交互作用时,单独考虑自变量与因变量的关系可能会导致结果的不显著。 因此,在回归不显著时,可以尝试引入交互作用项,以更全面地考虑自
- 样本量不足,回归系数的标准误差可能较大,计算t值或F值时出现较大的误差,从而导致回归系数的p值变大或出现NaN,进而导致回归系数不显著
解决办法:① 增加样本量② 减少自变量③ 使用非参数回归方法,降低对样本量的依赖性- 异常值可能对回归系数的计算产生影响,使得回归系数不显著。
- 该变量是无关变量:解决办法:直接剔除