数据结构-树与深度优先遍历
笔者在读书时,选择的专业是计算机科学,但和大家一样,在处理线性的问题时较为熟悉,但当自己在尝试理解树和图这种非线性结构时,就总无法深刻准确的理解,为此,也很苦恼很无奈,但也没有什么好的办法。这次趁着完成了《漫画算法》的阅读,再次总结一下关于书中树的内容,也许是几年的工作经历吧,让自己对于代码的编写和理解有了更多的体会,也了解到这种非线性结构的重要性。漫画算法这本书确实生动简洁,理解起来方便,大家对于数据结构感兴趣的,可以也买这本书读读,挺有意思的。图画的形式确实能增强理解性。
概念理解
树这种结构与链表不同,是因为每个节点的前驱都有一个,但后继节点有多个,即一对多。当然最常见的是后继节点只有两个,这样的树叫做二叉树,二叉树的应用非常的多,
- 二叉查找树
- 二叉排序树
树的概念如下:
术语
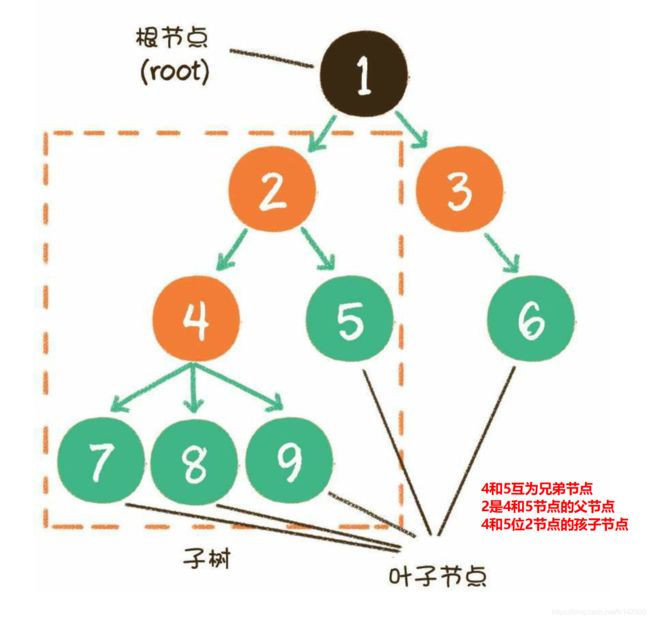
子树、根、叶子
层级
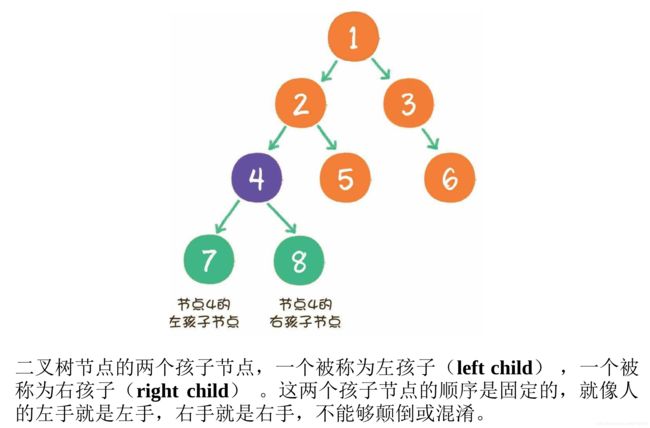
二叉树
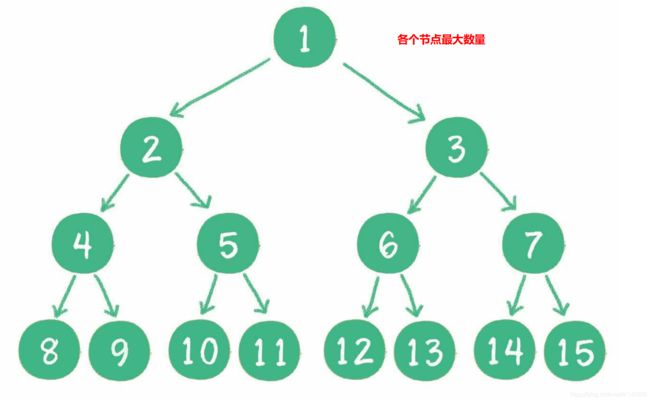
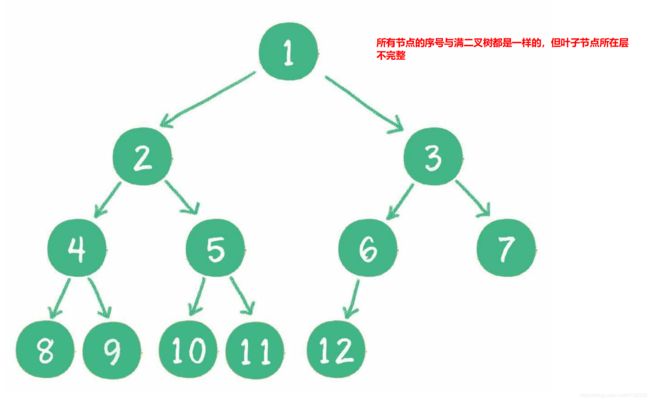
满二叉树和完全二叉树
存储方式
树的存储方式有两种
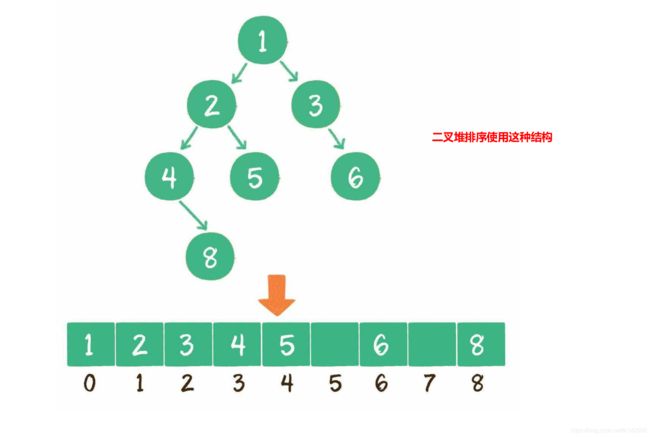
数组存储
二叉树数组排序中,根据节点的序号查找其父亲节点和孩子节点的规律如下图所示:
显然二叉堆的生成、上浮和下沉操作也是一个很重要的内容,需要好好的理解和梳理。
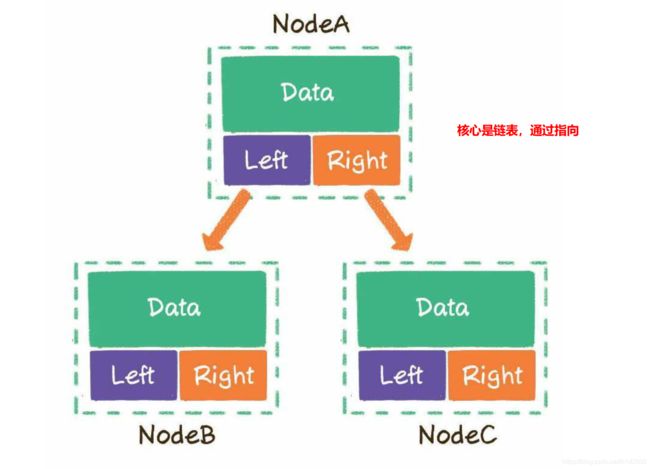
链式存储
链式存储,主要是节点元素同时携带了指向其左孩子和右孩子的引用。
深度优先遍历
树的遍历因为是非线性结构,通过某种遍历策略把非线性结构线性化,是关键的重点,也是理解的难点。
二叉树的遍历分为两种策略
- 深度优先
- 先根遍历
- 递归实现
- 非递归实现
- 栈
- 中根遍历
- 后根遍历
- 先根遍历
- 广度优先
- 队列
关于树的确定
给出一个中序序列,再给一个前序或后续序列,则可以确定一个个唯一的二叉树。
这里需要注意的是,两个序列中必须有一个中序序列才可以。 前序和后续组合无法确定唯一二叉树
二叉树的前(先)序中序和后序遍历 以及如何通过两个序列确定唯一二叉树
代码阐述
代码
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
/**
* 二叉树遍历
*
* @author songquanheng
* 2020/12/26-11:38
*/
public class BinaryTree {
private static class Node {
private int data;
private Node left;
private Node right;
public Node(int data) {
this.data = data;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
public static Node createBinaryTree(LinkedList<Integer> inputList) {
Node node = null;
if (inputList == null || inputList.isEmpty()) {
return null;
}
Integer data = inputList.removeFirst();
if (data == null) {
return node;
}
node = new Node(data);
node.left = createBinaryTree(inputList);
node.right = createBinaryTree(inputList);
return node;
}
public static void preOrderTraverse(Node root) {
if (root == null) {
System.out.print("null ");
return;
}
// 遍历当前节点
System.out.print(root.getData() + " ");
preOrderTraverse(root.left);
preOrderTraverse(root.right);
}
public static void inOrderTraverse(Node root) {
if (root == null) {
System.out.print("null ");
return;
}
inOrderTraverse(root.left);
System.out.print(root.getData() + " ");
inOrderTraverse(root.right);
}
public static void postOrderTraverse(Node root) {
if (root == null) {
// 说明节点是叶子结点的孩子
System.out.print("null ");
return;
}
// 以相同的策略完成对左子树的遍历
postOrderTraverse(root.left);
// 以相同的策略完成对右子树的遍历。
postOrderTraverse(root.right);
System.out.print(root.getData() + " ");
}
public static int depth(Node root) {
if (root == null) {
return 0;
}
int lDepth = depth(root.left);
int rDepth = depth(root.right);
return Math.max(lDepth, rDepth) + 1;
}
public static void main(String[] args) {
List<Integer> source = Arrays.asList(new Integer[]{3, 2, 9, null, null, 10, null, null, 8, null, 4});
LinkedList<Integer> inputList = new LinkedList<Integer>(source);
Node root = BinaryTree.createBinaryTree(inputList);
System.out.println("前序遍历");
// 3 2 9 null null 10 null null 8 null 4 null null
preOrderTraverse(root);
System.out.println();
System.out.println("中根遍历");
// null 9 null 2 null 10 null 3 null 8 null 4 null
inOrderTraverse(root);
System.out.println();
System.out.println("后根遍历");
// null null 9 null null 10 2 null null null 4 8 3
postOrderTraverse(root);
// 3
System.out.println("树的深度为: " + depth(root));
}
}
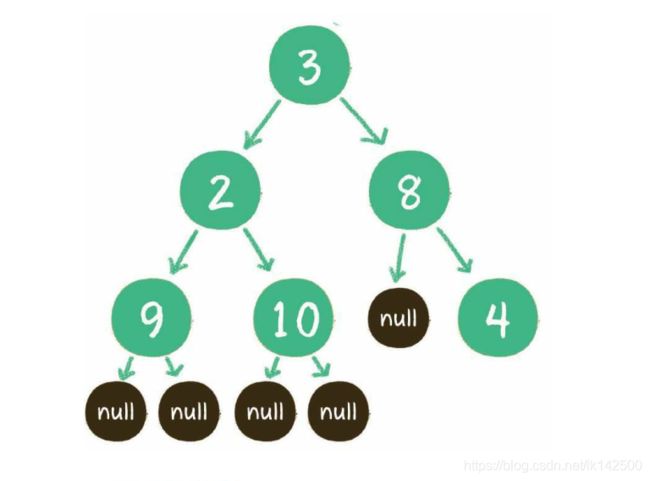
图解
代码采用递归的方式来创建一个二叉树,其实也可以不采用递归的方式,通过不断的插入节点,在插入节点时,说明节点的值和节点的父节点以及自身是二叉树的做孩子还是右孩子的方式也可以完成二叉树的创建。
代码中值得注意的是采用了前序遍历的序列来重建一个二叉树,把一个线性的链表转化成非线性的二叉树,链表节点的顺序恰恰是二叉树前序遍历的顺序。链表中空值,代表二叉树节点的左孩子和右孩子为空的情况
关于二叉树的遍历的思想,其实与斐波那契算法的思想是一样的,采用了分治的思想。之前一棵树节点数为N,左子树m个节点,右子树n个节点,访问整棵树的方法与访问各个子树的思想一样,因此把原先的问题规模降低了。
利用分治策略求解时,所需时间取决于分解后子问题的个数、子问题的规模大小等因素,而二分法,由于其划分的简单和均匀的特点,是经常采用的一种有效的方法,例如二分法检索。
运用分治策略解决的问题一般来说具有以下特点:
1、原问题可以分解为多个子问题
这些子问题与原问题相比,只是问题的规模有所降低,其结构和求解方法与原问题相同或相似。
2、原问题在分解过程中,递归地求解子问题
由于递归都必须有一个终止条件,因此,当分解后的子问题规模足够小时,应能够直接求解。
3、在求解并得到各个子问题的解后
应能够采用某种方式、方法合并或构造出原问题的解。
不难发现,在分治策略中,由于子问题与原问题在结构和解法上的相似性,用分治方法解决的问题,大都采用了递归的形式。在各种排序方法中,如归并排序、堆排序、快速排序等,都存在有分治的思想。
public static int depth(Node root) {
if (root == null) {
return 0;
}
int lDepth = depth(root.left);
int rDepth = depth(root.right);
return Math.max(lDepth, rDepth) + 1;
}
从结构上来看,深度优先遍历各种遍历方式,以及树的高度的查询均与分治的思想不谋而合。
总结
人间词话这本书已经阅读完成,最近在看米哈利·契克森米哈赖的发现心流的小书,书里面阐述了关于心流的概念,
心流隐含的含义,就是许多人形容自己表现最杰出时的那种水到渠成、不费吹灰之力的感觉,也就是运动家所谓的“巅峰状态”,艺术家及音乐家所谓的灵思泉涌。
想要获得心流的状态,有几个前提条件,1. 就是要有清晰的目标。2.要要规划,并且投入行动。3.要有立即回馈的。你可以在完成每一步骤之后,立刻判断自己是否有所改进。
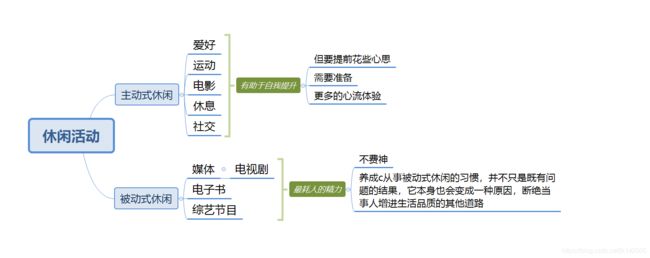
其中,米哈利也着重讲述了休闲活动对于个人生活品质的影响。
昨天一天的生活,白天较为充实,但晚上做好饭以后,就打开了《奔跑吧,黄河篇》看的很欢乐,虽然能带来短暂的振奋,但事后还是会黯然惆怅的。因为睡觉之前太过兴奋,而且下午也睡了太久的原因,导致自己在晚上再次熬夜了,今天上午自己其实有点精神不振的,毕竟失眠时候的自己,太容易分心和焦虑了。以后还是要坚持早睡的习惯。
大家也可以试试
每天给自己一个脱离手机,脱离屏幕的时间。坚持一段时间。
废话也不多说了,还是希望看到这个文章的各位,自己的生活能充实而丰富,日有所进,对于专业知识更加的扎实,不要像笔者一样,有点后悔2020年自己没什么目标,浑浑噩噩的又过了一年了。
关于树和遍历的内容,到这里就结束了,等之后自己再总结一下
- 使用栈来实现深度优先遍历
- 广度优先遍历
- 二叉堆
- 优先队列
的内容,这样把树的基本的内容就看完了。加油。因为再解决复杂问题时,太过重要,真的不花一番功夫真的不好理解。共勉
2020年12月27日11:48:42于奥克斯·时代未来之城