机器学习基础概念

大家好，我是一名正在学习机器学习的小白，最近在写一些关于机器学习基础概念的文章。如果你也对机器学习感兴趣，或者想要了解一些基础知识，欢迎来关注我哦！

定义

机器学习是一种人工智能的分支，它利用算法和统计模型来使计算机系统自动地从数据中学习和改进。机器学习的目标是让计算机系统能够自动地识别模式和规律，并根据这些规律来做出预测和决策。机器学习的应用非常广泛，包括图像识别、语音识别、自然语言处理、推荐系统、金融风险评估等领域。

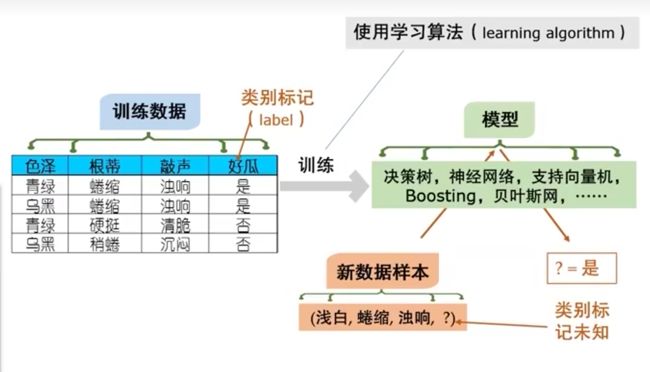
典型的机器学习过程

PAC理论

PAC（Probably Approximately Correct）理论是机器学习中的一个重要理论，它提供了一种理论保证，即在一定条件下，机器学习算法可以在有限的数据样本上学习到一个“近似正确”的模型。

PAC理论定义如下：

假设存在一个未知的概率分布D，它产生了一个样本空间X中的样本。我们想要学习一个函数f：X→Y，其中Y是输出空间。我们使用一个训练集S来学习f，S是从D中独立同分布采样得到的m个样本的集合。我们定义算法A在样本集S上的错误率为：

$$L_S(A)=\frac{1}{m}\sum _{i=1}^m{1}_{\{A(x_i)\ne f(x_i)\}}$$

其中，$1_{\{A(x_i)\ne f(x_i)\}}$是指示函数，当$A(x_i)\ne f(x_i)$时为1，否则为0。我们定义算法A的错误率为：

$$L_D(A)={\mathbb{P}}_{x\sim D}(A(x)\ne f(x))$$

PAC学习算法是指对于任意的$ϵ>0$和$\delta >0$，在样本数$m$满足以下条件时，存在一个算法A，使得它的错误率$L_D(A)$小于等于$ϵ$，并且它的错误率$L_S(A)$小于等于$ϵ$的概率大于等于$1-\delta$：

$$m\ge \frac{1}{ϵ}(\ln |H|+\ln \frac{1}{\delta })$$

其中，$H$是假设空间，它包含所有可能的函数$f$。

PAC理论的基本假设是：假设存在一个未知的目标函数f，它将输入空间中的每个实例映射到其相应的输出。机器学习算法的目标是学习一个假设函数h，它可以近似地表示目标函数f。PAC理论的目标是证明，当算法从有限的训练数据中学习时，它可以在一定概率下找到一个近似正确的假设函数h。

PAC理论的核心思想是通过控制假设函数的复杂度和训练数据的数量来控制学习算法的泛化误差。具体来说，PAC理论提出了以下三个概念：

1. 可近似正确性（Approximation）：假设函数h可以在一定误差范围内近似地表示目标函数f。

2. 可学习性（Learnability）：学习算法可以从有限的训练数据中学习到一个近似正确的假设函数h。

3. 可泛化性（Generalization）：学习到的假设函数h可以在新的未见过的数据上表现良好。

PAC理论提供了一些定理，例如Hoeffding不等式和VC维理论，可以帮助我们分析学习算法的可学习性和可泛化性。这些定理可以帮助我们选择合适的学习算法、确定训练数据的数量和质量、控制模型的复杂度等。

总之，PAC理论是机器学习中的一个重要理论，它提供了一种理论保证，即在一定条件下，机器学习算法可以在有限的数据样本上学习到一个“近似正确”的模型。

P问题与NP问题

P问题和NP问题是计算机科学中的两个重要问题，它们涉及到计算复杂性和算法效率的问题。

P问题是指在多项式时间内可以解决的问题，也就是说，存在一个多项式时间的算法可以在有限时间内解决这个问题。例如，排序、查找、加减乘除等基本算法都是P问题。

多项式时间的算法是指在输入规模为n的情况下，算法的运行时间可以表示为一个多项式函数，即O(n^k)，其中k为常数。这种算法的运行时间随着输入规模的增加而增加，但增长速度不会超过一个多项式函数。

多项式时间的算法通常被认为是高效的算法，因为它们的运行时间不会随着输入规模的增加而呈指数级增长。在实际应用中，多项式时间的算法通常被认为是可接受的，而指数时间的算法则往往被认为是不可接受的。

许多经典的算法，如排序算法、图论算法等，都有多项式时间的实现。然而，有些问题，如NP问题，目前还没有已知的多项式时间算法。

NP问题是指在多项式时间内可以验证解答的问题，也就是说，如果一个解答是正确的，那么可以在多项式时间内验证它的正确性。但是，目前并没有已知的多项式时间算法可以解决NP问题。例如，旅行商问题、背包问题、图着色问题等都是NP问题。

P问题和NP问题之间的关系是一个重要的问题，它涉及到计算机科学中的一个著名问题——P=NP问题。P=NP问题是指，是否存在一个多项式时间算法可以解决所有的NP问题，也就是说，P问题和NP问题是等价的。但是，目前并没有任何证据证明P=NP，这个问题仍然是计算机科学中的一个未解决问题。

总之，P问题和NP问题是计算机科学中的两个重要问题，它们涉及到计算复杂性和算法效率的问题，对于计算机科学的发展和应用具有重要的意义。

机器学习术语列表

数据集相关

• 数据集（Dataset）：用于训练和测试模型的数据集合。
• 样本（Sample）：数据集中的一个数据点。
• 特征（Feature）：数据集中每个样本的属性或特征。
• 标签（Label）：数据集中每个样本对应的输出或目标值。
• 训练集（Training set）：用于训练模型的数据集。
• 验证集（Validation set）：用于调整模型超参数的数据集。
• 测试集（Test set）：用于评估模型性能的数据集。

模型相关

• 模型（Model）：用于预测或分类的算法或函数。
• 参数（Parameter）：模型中需要学习的变量。
• 超参数（Hyperparameter）：模型中需要手动设置的参数。
• 损失函数（Loss function）：用于衡量模型预测结果与真实值之间的差距。
• 优化算法（Optimization algorithm）：用于更新模型参数的算法。
• 监督学习（Supervised learning）：使用有标签数据进行训练的机器学习方法。
• 无监督学习（Unsupervised learning）：使用无标签数据进行训练的机器学习方法。
• 半监督学习（Semi-supervised learning）：同时使用有标签和无标签数据进行训练的机器学习方法。
• 强化学习（Reinforcement learning）：通过与环境交互来学习最优策略的机器学习方法。

性能评估相关

• 准确率（Accuracy）：模型预测正确的样本数占总样本数的比例。
• 精确率（Precision）：模型预测为正样本且正确的样本数占预测为正样本的样本数的比例。
• 召回率（Recall）：模型预测为正样本且正确的样本数占实际为正样本的样本数的比例。
• F1值（F1 score）：精确率和召回率的调和平均数。
• ROC曲线（ROC curve）：以假正率为横轴，真正率为纵轴的曲线，用于评估二分类模型性能。
• AUC值（AUC）：ROC曲线下的面积，用于评估二分类模型性能。

其他

• 特征工程（Feature engineering）：对原始数据进行处理和转换，以提取更有用的特征。
• 过拟合（Overfitting）：模型在训练集上表现良好，但在测试集上表现较差的现象。
• 欠拟合（Underfitting）：模型无法在训练集上获得足够好的拟合效果的现象。
• 交叉验证（Cross-validation）：将数据集分成多个子集，轮流使用每个子集作为验证集，其余子集作为训练集，以评估模型性能。
• 网格搜索（Grid search）：通过遍历超参数的所有可能组合，寻找最优超参数的方法。

归纳偏好

归纳偏好是指机器学习算法在学习过程中对某些假设的倾向或偏好。这些偏好可能是由于算法本身的设计、数据集的特征或者先验知识等因素所导致的。

例如，决策树算法在学习过程中倾向于选择简单的树结构，因为简单的树结构更容易解释和理解。而神经网络算法则倾向于选择具有多个隐藏层的复杂模型，因为这些模型可以更好地拟合复杂的非线性关系。

在机器学习中设置偏置是为了让模型更加灵活和准确。偏置可以帮助模型更好地拟合数据，提高模型的预测能力。例如，在线性回归模型中，偏置可以用来调整模型的截距，使得模型更好地拟合数据。在神经网络模型中，偏置可以用来调整每个神经元的激活阈值，从而提高模型的准确性。

奥卡姆剃刀

奥卡姆剃刀（Occam’s Razor）是一种科学原则，也被称为简洁性原则。它的基本思想是，如果有多种解释可以解释某个现象，那么最简单的解释往往是最可信的。在机器学习中，奥卡姆剃刀原则通常被用来指导模型选择和特征选择，即在多个模型或特征之间选择最简单的那个，以避免过度拟合和提高模型的泛化能力。

NFL定理

NFL定理（No Free Lunch Theorem）是指在所有问题和算法的平均性能上，没有任何一种算法比其他算法更好。NFL定理表明，对于所有问题，不存在一种算法能够在所有情况下都表现最好。因此，在选择算法时，需要考虑问题的特点和算法的适用性。

NFL定理的含义是，如果一个算法在某些问题上表现得很好，那么它在其他问题上的表现就可能不如其他算法。因此，在机器学习中，需要根据具体问题的特点选择合适的算法，而不能盲目追求某种算法的“最优性”。

NFL定理的证明比较复杂，需要使用概率和信息论等数学工具。但是，其基本思想可以用简单的语言来表达：没有免费的午餐。也就是说，如果想要在某些问题上表现得很好，就必须在其他问题上付出代价。

泛化能力

泛化能力是指机器学习模型在处理新数据时的表现能力。一个具有良好泛化能力的模型能够在未见过的数据上表现出与训练数据相似的性能，而不是仅仅在训练数据上表现良好。泛化能力是机器学习模型的重要指标之一，因为它决定了模型的实用性和可靠性。

过拟合和欠拟合是机器学习中常见的两个问题，它们都与模型的泛化能力有关。

过拟合（overfitting）

指的是模型在训练集上表现很好，但在测试集上表现很差的情况。这是因为模型过于复杂，过度拟合了训练数据，导致对新数据的泛化能力较差。过拟合的表现是训练误差很小，但测试误差很大。

欠拟合（underfitting）

指的是模型在训练集和测试集上表现都不好的情况。这是因为模型过于简单，无法捕捉数据中的复杂关系，导致对新数据的泛化能力较差。欠拟合的表现是训练误差和测试误差都很大。

泛化能力是指模型对新数据的适应能力，即模型在训练集之外的数据上的表现能力。泛化能力好的模型能够很好地适应新数据，而泛化能力差的模型则容易出现过拟合或欠拟合的问题。

为了解决过拟合和欠拟合的问题，可以采取以下措施：

1. 过拟合：增加训练数据、减少模型复杂度、正则化等。

2. 欠拟合：增加模型复杂度、增加特征、减少正则化等。

综上所述，泛化能力是机器学习中非常重要的概念，它关系到模型的实际应用效果。在模型训练过程中，需要注意平衡模型的复杂度和泛化能力，以达到最佳的预测效果。

评估方法

在机器学习中，测试集是用于评估模型性能的数据集。测试集应该与训练集互斥，即测试集中的数据不应该出现在训练集中。以下是获取测试集的几种常见方法：

留出法（Hold-Out Method）

留出法是最简单的获取测试集的方法，它将数据集分为训练集和测试集两部分。通常将数据集的70%~ 80%作为训练集，剩余的20%~30%作为测试集。

具体实现过程如下：

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

其中，X和y分别是特征和标签，test_size表示测试集占比，random_state是随机种子，用于保证每次划分的结果一致。

交叉验证法（Cross-Validation）

交叉验证法是一种更加稳健的获取测试集的方法，它将数据集分为k个子集，每次使用其中一个子集作为测试集，其余子集作为训练集，重复k次，最终得到k个模型的性能评估结果的平均值。

交叉验证法和留出法都是常用的模型评估方法，但它们的实现方式和评估效果有所不同。

交叉验证法是将数据集分成k个大小相似的互斥子集，每次用其中一个子集作为验证集，剩下的k-1个子集作为训练集，重复k次，每次都选择不同的验证集，最终得到k个模型的评估结果的平均值。交叉验证法的优点是能够更充分地利用数据，减小模型评估的方差，但缺点是计算量较大，需要多次训练模型。

留出法是将数据集分成训练集和测试集两部分，其中训练集用于训练模型，测试集用于评估模型的性能。留出法的优点是计算量较小，易于实现，但缺点是可能会出现过拟合或欠拟合的情况，因为测试集的数据可能无法代表整个数据集的分布。

总的来说，交叉验证法更适合用于模型选择和调参，留出法更适合用于模型的最终评估。

具体实现过程如下：

from sklearn.model_selection import cross_val_score, KFold

kfold = KFold(n_splits=10, shuffle=True, random_state=42)
scores = cross_val_score(model, X, y, cv=kfold)

其中，n_splits表示将数据集分为几个子集，shuffle表示是否打乱数据集，random_state是随机种子，model是要评估的模型。

自助法（Bootstrap）

自助法是一种通过有放回抽样的方式获取测试集的方法，它将数据集中的一部分样本重复采样，得到一个新的数据集，新数据集中的样本数与原数据集相同，但有些样本可能出现多次，有些样本可能没有出现。这样，新数据集中未出现的样本就可以作为测试集。

具体实现过程如下：

from sklearn.utils import resample

X_train, X_test, y_train, y_test = resample(X, y, test_size=0.3, random_state=42)

其中，test_size表示测试集占比，random_state是随机种子。

留一法（Leave-One-Out）

留一法是一种特殊的交叉验证方法，它将数据集中的每个样本都作为测试集，其余样本作为训练集，重复n次，n为数据集中样本的个数。由于留一法需要重复n次训练模型，因此计算量较大，一般只在数据集较小的情况下使用。具体实现过程如下：

from sklearn.model_selection import LeaveOneOut

loo = LeaveOneOut()
scores = cross_val_score(model, X, y, cv=loo)

其中，model是要评估的模型。

以上是获取测试集的几种常见方法，不同的方法适用于不同的数据集和模型，需要根据具体情况选择合适的方法。

性能度量

在机器学习中，TP、TN等表达通常用于表示分类模型的性能度量指标。具体解释如下：

• TP（True Positive）：真正例，表示模型将正样本正确地预测为正样本的数量。
• TN（True Negative）：真负例，表示模型将负样本正确地预测为负样本的数量。
• FP（False Positive）：假正例，表示模型将负样本错误地预测为正样本的数量。
• FN（False Negative）：假负例，表示模型将正样本错误地预测为负样本的数量。

在机器学习中，性能度量是评估模型预测能力的重要指标。常用的性能度量包括准确率、精确率、召回率、F1值、ROC曲线和AUC值等。

1. 准确率（Accuracy）

准确率是指模型预测正确的样本数占总样本数的比例。

公式：$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$

其中，TP表示真正例，TN表示真负例，FP表示假正例，FN表示假负例。

2. 精确率（Precision）

精确率是指模型预测为正例的样本中，真正例的比例。

公式：$Precision=\frac{TP}{TP+FP}$

3. 召回率（Recall）

召回率是指真正例中被模型预测为正例的比例。

公式：$Recall=\frac{TP}{TP+FN}$

4. F1值

F1值是精确率和召回率的调和平均数，用于综合评价模型的性能。

公式：$F1=\frac{2\ast Precision\ast Recall}{Precision+Recall}$

5. ROC曲线

ROC曲线是以假正例率（FPR）为横坐标，真正例率（TPR）为纵坐标的曲线，用于评估二分类模型的性能。

6. AUC值

AUC值是ROC曲线下的面积，用于衡量模型预测能力的综合性能。

以上是机器学习中常用的性能度量指标及其公式。在实际应用中，不同的问题需要选择不同的性能度量指标来评估模型的性能。

比较检验

比较检验是机器学习中用于比较不同模型性能的一种方法。在比较检验中，我们通常会使用一些统计指标来比较不同模型的性能，例如准确率、精确率、召回率、F1分数等。比较检验的目的是找到最优的模型，以便在实际应用中获得最佳的性能。

比较检验通常包括以下步骤：

1. 选择要比较的模型：首先需要选择要比较的模型，这些模型可以是不同的算法、不同的超参数组合或不同的特征集合等。

2. 划分数据集：将数据集划分为训练集和测试集，通常采用交叉验证的方法来划分数据集。

3. 训练模型：使用训练集训练模型，并使用测试集评估模型性能。

4. 比较模型：使用统计指标比较不同模型的性能，例如准确率、精确率、召回率、F1分数等。

5. 选择最优模型：根据比较结果选择最优的模型，并在实际应用中使用该模型。

比较检验是机器学习中非常重要的一部分，它可以帮助我们选择最优的模型，并在实际应用中获得最佳的性能。

线性回归

什么是线性回归

线性回归是一种常见的机器学习算法，用于建立输入变量和输出变量之间的线性关系模型。它的背景可以追溯到19世纪初，由法国数学家Adrien-Marie Legendre提出。Legendre在研究天体运动时，发现了一种方法来拟合数据，这就是线性回归的雏形。

在线性回归中，我们假设输入变量和输出变量之间存在线性关系，即输出变量可以表示为输入变量的线性组合加上一个常数项。这个关系可以用以下公式表示：

$$y=b_0+b_1{x}_1+b_2{x}_2+...+b_n{x}_n$$

其中，$y$是输出变量，$x_1$、$x_2$、…、$x_n$是输入变量，$b_0$、$b_1$、$b_2$、…、$b_n$是模型的参数，也称为回归系数。

离散属性的序的关系指的是离散属性之间存在一定的大小关系，例如衣服的尺码大小，可以分为S、M、L、XL等，其中S比M小，M比L小，L比XL小。这种大小关系可以用数值来表示，但是这些数值并不是真正的数值，而是代表了不同的类别。

在处理离散属性的序的关系时，可以采用以下方法：

1. 标签编码：将不同的类别用数字表示，例如将S编码为1，M编码为2，以此类推。

2. 独热编码：将每个类别转换为一个二进制向量，向量中只有一个元素为1，其余元素为0，例如将S编码为[1,0,0,0]，M编码为[0,1,0,0]，以此类推。

需要注意的是，如果离散属性之间不存在大小关系，则不能使用标签编码或独热编码，而应该使用其他方法，例如哈希编码或二进制编码。

线性回归的目标是找到一组最优的回归系数，使得模型的预测值与实际值之间的误差最小化。这个误差通常用最小二乘法来计算，即将预测值与实际值之间的差平方求和，然后取平均值（均方误差）。

在实际应用中，我们通常会将数据集分为训练集和测试集，用训练集来训练模型，然后用测试集来评估模型的性能。常用的性能度量指标包括均方误差（MSE）、均方根误差（RMSE）和平均绝对误差（MAE）等。

均方误差（MSE）

均方误差（Mean Squared Error，MSE）是衡量预测值与真实值之间差异的一种常用指标。它计算的是预测值与真实值之间差异的平方的平均值。

均方误差的公式如下：

$$MSE=\frac{1}{n}\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2$$

其中，$y_i$ 是真实值，$\widehat{y_i}$ 是预测值，$n$ 是样本数量。

MSE 的值越小，说明预测值与真实值之间的差异越小，模型的预测能力越好。

均方根误差（RMSE）

均方根误差（Root Mean Squared Error，RMSE）是均方误差的平方根。它的计算方法与均方误差相同，只是在最后将均方误差的结果开方。

均方根误差的公式如下：

$$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2}$$

与均方误差相比，均方根误差更加直观，因为它的单位与真实值的单位相同。RMSE 的值越小，说明预测值与真实值之间的差异越小，模型的预测能力越好。

平均绝对误差（MAE）

平均绝对误差（Mean Absolute Error，MAE）是另一种衡量预测值与真实值之间差异的指标。它计算的是预测值与真实值之间差异的绝对值的平均值。

平均绝对误差的公式如下：

$$MAE=\frac{1}{n}\sum _{i=1}^n|y_i-\widehat{y_i}|$$

与均方误差和均方根误差相比，平均绝对误差更加鲁棒，因为它不受离群值的影响。但是，它也更加不敏感，因为它没有考虑预测值与真实值之间的差异的平方。

多元线性回归

广义线性模型

广义线性模型（Generalized Linear Model，GLM）是一种广泛应用于统计学和机器学习领域的模型，它是线性模型的扩展，可以处理非正态分布的响应变量和非线性关系。

GLM的基本形式是：假设响应变量y服从某个分布，其均值与自变量x之间存在某种函数关系，即：

$$y\sim F(\mu (x))$$

其中，F是分布函数，$\mu (x)$是均值函数，x是自变量。

GLM的三个基本要素是：分布族、链接函数和线性预测子。

1. 分布族

GLM假设响应变量y来自某个分布族，常见的分布族有正态分布、泊松分布、二项分布、伽马分布等。

2. 链接函数

链接函数是将均值函数$\mu (x)$与线性预测子$\eta (x)$联系起来的函数，它的作用是将线性预测子的范围映射到响应变量的范围内。常见的链接函数有：

• 逆正弦函数（Inverse Sine Function）：适用于正态分布；
• 对数函数（Log Function）：适用于泊松分布、二项分布、伽马分布等；
• 逆双曲正切函数（Inverse Hyperbolic Tangent Function）：适用于二项分布。

3. 线性预测子

线性预测子是自变量x的线性组合，它的形式为：

$$\eta (x)={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+...+{\beta }_p{x}_p$$

其中，${\beta }_0,{\beta }_1,{\beta }_2,...,{\beta }_p$是模型的系数，$x_1,x_2,...,x_p$是自变量。

GLM的优点是可以处理非正态分布的响应变量和非线性关系，同时具有较好的解释性和可解释性。缺点是需要选择合适的分布族和链接函数，并且需要进行模型检验和诊断。

对率回归

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5IioEO5v-1685599184218)(C:\Users\tgy18\AppData\Roaming\Typora\typora-user-images\image-20230522223042387.png)]

对数几率函数，对率回归（Logistic Regression）是一种常见的分类算法，它的目的是根据已知的数据集，建立一个能够将新的数据分类的模型。对率回归的基本思想是通过对数据进行逻辑回归分析，得到一个能够将数据分类的函数，然后利用该函数对新的数据进行分类。

对率回归的模型是一个线性模型，它的输出值是一个概率值，表示该样本属于某个类别的概率。对率回归的模型可以用以下公式表示：

$$P(y=1|x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

其中，$x$ 是输入特征向量，$\theta$ 是模型参数向量，$y$ 是输出标签，$P(y=1|x)$ 表示给定输入 $x$，输出标签为 $1$ 的概率。

对率回归的训练过程是通过最大化似然函数来确定模型参数 $\theta$。最大化似然函数的过程可以通过梯度下降等优化算法来实现。

对率回归的优点是模型简单、易于实现和解释，适用于二分类和多分类问题。缺点是对于非线性分类问题，需要进行特征工程或者使用其他的分类算法。

求解过程

对率回归是一种二分类模型，它的目标是通过已知的训练数据集，建立一个能够将新的数据样本分类为正类或负类的模型。对率回归的核心思想是通过对数据进行逻辑回归，将线性回归的输出映射到[0,1]区间内，从而得到样本属于正类的概率。

对率回归的数学模型可以表示为：

$$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

其中，$h_{\theta }(x)$表示样本$x$属于正类的概率，$\theta$表示模型的参数，$x$表示样本的特征向量。

对率回归的目标是最大化似然函数，即：

$$L(\theta )=\prod _{i=1}^m{h}_{\theta }(x^{(i)}{)}^{y^{(i)}}(1-h_{\theta }(x^{(i)}){)}^{1-y^{(i)}}$$

最大化似然函数是一种常用的参数估计方法，它的目的是通过已知的样本数据，来估计未知的参数值，使得样本数据出现的概率最大化。

假设我们有一个样本数据集 $D=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_n,y_n)\}$，其中 $x_i$ 是输入变量，$y_i$ 是输出变量，$i=1,2,\cdots ,n$。我们假设 $y_i$ 的分布是由一个参数向量 $\theta$ 决定的，即 $p(y_i|x_i,\theta )$。那么，对于给定的样本数据集 $D$，我们可以定义似然函数 $L(\theta |D)$，表示在给定参数向量 $\theta$ 的情况下，样本数据集 $D$ 出现的概率：

$$L(\theta |D)=\prod _{i=1}^{n}p(y_i|x_i,\theta )$$

我们的目标是找到一个最优的参数向量 ${\theta }^{\ast }$，使得似然函数 $L(\theta |D)$ 最大化，即：

$${\theta }^{\ast }=\arg \underset{\theta }{\max }L(\theta |D)$$

这个问题可以通过最大化对数似然函数来解决，即：

$${\theta }^{\ast }=\arg \underset{\theta }{\max }\log L(\theta |D)$$

因为对数函数是单调递增的，所以最大化对数似然函数等价于最大化似然函数。最大化对数似然函数的过程可以使用梯度下降等优化算法来实现。

其中，$m$表示训练样本的数量，$y^{(i)}$表示样本$x^{(i)}$的标签，如果$x^{(i)}$属于正类，则$y^{(i)}=1$，否则$y^{(i)}=0$。

对于似然函数，我们可以取对数，得到对数似然函数：

$$l(\theta )=\sum _{i=1}^m[y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]$$

对数似然函数是一个凸函数，可以使用梯度下降等优化算法求解。对于对数似然函数的梯度，可以表示为：

$$\frac{\partial l(\theta )}{\partial {\theta }_j}=\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$

根据梯度下降算法，我们可以更新参数$\theta$：

$${\theta }_j:={\theta }_j-\alpha \frac{\partial l(\theta )}{\partial {\theta }_j}$$

其中，$\alpha$表示学习率。

通过不断迭代更新参数$\theta$，我们可以得到最优的模型参数，从而实现对新数据的分类。

总结一下，对率回归的求解过程可以概括为以下几个步骤：

1. 定义对率回归的数学模型，即$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$。

2. 定义似然函数，即$L(\theta )={\prod }_{i=1}^m{h}_{\theta }(x^{(i)}{)}^{y^{(i)}}(1-h_{\theta }(x^{(i)}){)}^{1-y^{(i)}}$。

3. 取对数，得到对数似然函数，即$l(\theta )={\sum }_{i=1}^m[y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]$。

4. 求解对数似然函数的梯度，即$\frac{\partial l(\theta )}{\partial {\theta }_j}={\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$。

5. 使用梯度下降等优化算法更新参数$\theta$，即${\theta }_j:={\theta }_j-\alpha \frac{\partial l(\theta )}{\partial {\theta }_j}$。

6. 重复步骤4和步骤5，直到收敛。

7. 得到最优的模型参数$\theta$，从而实现对新数据的分类。

$$P{E}_{(pos,2i+1)}=cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)$$
)}}$。

3. 取对数，得到对数似然函数，即$l(\theta )={\sum }_{i=1}^m[y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]$。

4. 求解对数似然函数的梯度，即$\frac{\partial l(\theta )}{\partial {\theta }_j}={\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$。

5. 使用梯度下降等优化算法更新参数$\theta$，即${\theta }_j:={\theta }_j-\alpha \frac{\partial l(\theta )}{\partial {\theta }_j}$。

6. 重复步骤4和步骤5，直到收敛。

7. 得到最优的模型参数$\theta$，从而实现对新数据的分类。

$$P{E}_{(pos,2i+1)}=cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)$$

正则项

正则项是机器学习中用来控制模型复杂度的一种技术。正则项通常加到模型的损失函数中，以惩罚模型参数的绝对值（L1正则化）或平方（L2正则化）。在进行优化时，加入正则项就相当于在损失函数中引入一个先验偏好，帮助模型更好地捕捉数据之间的潜在关系，避免过拟合的情况。

在机器学习中，所谓的极值化指的是模型参数取极大值或极小值的情况，也就是出现了过拟合或者欠拟合的情况。追求过高或者过低的模型参数会导致模型对训练数据过于敏感，而无法泛化到新数据上。过于极值化的模型参数可能导致模型过于复杂，在训练数据上得到很好的性能，但是在测试数据上表现差。因此，为了得到泛化性能更好的模型，我们需要控制模型参数的极值化程度，而正则化技术就是能够达到这个目的的一种方法。

通常在模型训练中，我们最小化损失函数（loss function），即通过优化损失函数中的参数来最小化误差。当模型过拟合数据时，优化过程中会使得模型的参数变得极值化，导致模型泛化能力下降，也就是说它对新来的数据表现不佳。因此，我们需要将正则项加入到损失函数中，在最小化损失函数的同时，也会减少参数的绝对值，保证了模型的泛化能力。

L1和L2正则项的区别在于惩罚项是绝对值还是平方，L2正则化可防止过严格的约束，更加平滑。

支持向量机

支持向量机（Support Vector Machine，SVM）是一种监督式学习算法，常用于分类和回归问题。在分类问题中，SVM的目标是将数据分为不同的类别，同时最大化分类的间隔（即将分类的边界尽可能远离数据），从而提高分类的准确性和泛化能力。SVM的核心思想是将数据映射到高维空间，然后在高维空间中找到一个最优的超平面，将不同类别的数据分开。这个最优的超平面被称为分隔超平面，且由一些支持向量组成，这些支持向量是离分隔超平面最近的数据点。

SVM可以使用不同的核函数来处理非线性问题，如多项式核、高斯核等。在进行模型评估时，常用的指标包括准确率、精确率、召回率和F1分数。

支持向量

支持向量是指距离分隔超平面最近的那些训练样本点。简单来说，支持向量就是决策边界的关键点。

软间隔

软间隔是机器学习中支持向量机（SVM）算法中的一种概念，用来处理训练数据中存在噪声或异常值的情况。在正常的SVM算法中，数据点需要完美地分开，但在现实情况下，我们经常会遇到一些数据点无法完美分开的情况。这时，我们可以使用软间隔来容忍一些噪声或异常值。

具体来说，在软间隔的情况下，我们允许一些数据点位于分隔平面错误的一侧或跨越分隔线，但要进行最小化。换句话说，我们减少我们的目标是最大化分类准确性的同时，允许一些错误的分类。为了实现这一点，通常需要为SVM模型添加一个惩罚项，该惩罚项会惩罚那些距离分隔平面过于靠近的数据点。

在实践中，软间隔可以提高SVM模型的鲁棒性，减少误差率和适应度。然而，需要注意的是，增加软间隔的复杂度也会增加训练时间和计算成本。因此，当处理大规模数据时，必须仔细平衡准确性和复杂性之间的关系。

正则化

软间隔和正则化是SVM算法中常用的两种方法，它们都可以用来提高模型的泛化能力和避免过拟合问题。

正则化可以通过限制模型的复杂度来避免过拟合问题。在SVM中，正则化通常是通过引入一个惩罚参数来实现的，这个惩罚参数可以影响模型对低频特征的关注程度。正则化和软间隔都可以防止模型过拟合，但正则化更多地关注模型的复杂度和稳定性。

软间隔和正则化是可以同时使用的。在实际应用中，通常选择合适的正则化参数和松弛变量参数来平衡模型的复杂度和准确性，以达到最优的模型性能。

加入损失函数

在软间隔的实现中，通常会引入一个损失函数，用于衡量模型预测错误的程度。常用的损失函数包括hinge loss和squared hinge loss等。

在SVM中，常用的损失函数是hinge loss，它的形式为：

L(y,f(x)) = max(0, 1 - y*f(x))

其中，y表示样本的真实标签，f(x)表示模型对样本的预测结果。当预测正确时，损失为0；当预测错误时，损失为1-y*f(x)。

核函数

核函数是一种数学函数，它可以将数据从低维空间映射到高维空间，从而使得数据在高维空间中更容易被分类或回归。核函数在支持向量机（SVM）和其他某些机器学习算法中经常用作非线性函数。每个核函数都有自己的一组参数，这些参数需要通过交叉验证等技术进行调整，以优化模型性能。

在机器学习中，最常用的核函数是：

1. 线性核函数：将数据映射到它们本来的特征空间。

2. 多项式核函数：将数据映射到更高维的特征空间，使数据更容易被分类或回归。

3. 高斯径向基函数（RBF）核函数：将数据投射到无限维特征空间中，可以处理高度非线性的数据分类或回归问题。

另外还有其他一些核函数，如拉普拉斯核、Sigmoid核函数等，它们也都有自己的特点和适用范围。其他机器学习算法比如KNN、聚类分析等也可以使用核函数来进行非线性变换。

贝叶斯分类器

贝叶斯分类器（Bayesian classifier）是一种根据贝叶斯定理来进行分类的算法。它是一种基于统计学习理论的分类器，经常被用于文本分类、垃圾邮件过滤、情感分析等任务中。

贝叶斯分类器基于先验概率和条件概率来进行分类。在分类之前，我们需要训练模型，通过学习样本数据集来确定各个类别的先验概率和条件概率。

先验概率和条件概率都是概率论中基本的概念。先验概率是指在没有任何其他信息的情况下，我们对某个事件发生的概率的初始估计；条件概率是指在已知某些信息的情况下，我们对某个事件发生的概率所做的修正估计。下面是先验概率和条件概率的公式：

先验概率公式：P(A)

条件概率公式：P(B|A) = P(A and B) / P(A)

其中，P(A)表示事件A的先验概率，P(B|A)表示在知道事件A已经发生的条件下，事件B发生的概率，P(A and B)表示事件A和事件B同时发生的概率，P(A)则是为了计算条件概率而需要的事件A的先验概率。

通过对这些概率的计算，可以给出数据点属于不同类别的概率，然后根据概率大小来进行分类。

具体来说，对于给定的一个数据点，我们需要对其所有特征的条件概率进行计算，然后将它们乘起来得到属于各个类别的概率。最后，根据概率大小来判断数据点属于哪个类别。

贝叶斯分类器通常具有很好的分类效果，而且易于实现和解释。它在大量的实际应用中已经得到了验证，是一种非常重要的分类器算法。

贝叶斯决策论

贝叶斯决策论（Bayesian decision theory）是一种基于概率模型的决策方法。它将不确定性引入到决策分析中，并考虑到各种不确定性因素，如决策的后果、各种可能的行动以及每种行动可能发生的概率。

贝叶斯决策论的核心思想是：在决策前，先估计各种可能结果的概率，然后根据这些概率进行决策。这一过程包含了一个建模过程和一个推断过程。

在建模过程中，我们需要选择一个合适的概率模型来描述问题。这个模型应该能够描述已知的数据，并可以推断未知的数据。在推断过程中，我们需要使用贝叶斯公式来计算后验概率分布，从而得到最优决策，即具有最大期望效用的决策。

拉普拉斯修正

拉普拉斯修正是一种用于处理概率估计中零频项的技术。当我们使用最小二乘法或极大似然估计等方法，对观测数据或样本进行概率估计时，通常会遇到概率为零的情况。这时，我们可以采用拉普拉斯修正来解决这个问题。

拉普拉斯修正的基本思想是在计算概率分布的时候，对每个计数加上一个偏置。这样，我们就可以在统计上假定每个可能的事件至少发生了一次，从而避免零概率问题。具体来说，我们可以将每个计数加上一个特定的值（通常是1），再进行概率计算。

例如，考虑一个二项分布的情况，我们希望计算参数p的极大似然估计。在这种情况下，如果训练集中没有观测到一个事件，那么参数p的估计值就会为零。但实际上，这个事件可能会在测试数据中出现，所以我们不应该将它的概率估计为零。使用拉普拉斯修正，对于每个计数，我们都可以将其增加1，这样我们就可以得到一个更为准确的概率估计。

拉普拉斯修正可以表示为如下公式：
$$\hat{p}=\frac{n_i+1}{N+m}$$
其中，$n_i$表示观测到的事件$i$的计数，$N$表示总的观测样本数，$m$表示事件类别的总数，$\hat{p}$表示修正后的概率估计。

拉普拉斯修正不是唯一的解决零频项问题的方法，还有其他的方法，例如贝叶斯方法、加权平均和Katz回退平滑等。

朴素贝叶斯与半朴素贝叶斯

朴素贝叶斯算法假设特征相互独立，可以简化分类过程并使用小数据集进行训练。它计算先验概率和条件概率来得出后验概率，然后将数据分配到概率最大的类别。但实际情况中特征之间不总是独立的，影响了分类效果。半朴素贝叶斯算法通过选择主要特征和相关特征，并考虑他们的相关性，提高了分类准确度。主要特征和分类目标高度相关，相关特征与分类目标相关性较小。使用朴素贝叶斯算法对主要特征进行分类，对于相关特征则考虑它们与主要特征之间的相关性。这样，半朴素贝叶斯算法既简单又能更好地应对特征相关性的问题。

集成学习

集成学习（Ensemble Learning）是一种将多个基础学习器（Base Learner）组合在一起，形成强学习器（Strong Learner）进行预测或分类的方法。它可以通过结合多个弱分类器（Weak Classifier）来提高分类准确率，因为每个弱分类器可能只能对某个子问题做出良好的预测，但将多个弱分类器进行组合，可以产生比单个分类器更为准确的预测结果。集成学习有多种实现方式，如投票、平均等。其中最常见的分类器集成方法是“Bagging”和“Boosting”。

Bagging

“Bagging”是Bootstrap Aggregating的缩写，也叫自助采样聚合，是一种基于自助采样的集成学习方法。它是将训练集进行有放回地采样生成多个不同的训练集，每个子集都是通过有放回的采样从原始训练集中采样得到的，然后基于每个子集训练出一个基础模型，最后将这些基础模型合成一个集成模型。由于采样集合的随机性，每个基础模型的训练数据有所不同，这样可以减少过拟合问题。

Boosting

是一种基于迭代的集成学习方法，它训练一系列的分类器，不断迭代地调整、改进它们的分类能力，使它们能够进行更准确的分类。 在 Boosting 中，每个分类器负责处理数据中分错的那一部分。在每次迭代中，实例权重将会被调整，分错较多的实例将获得较高的权重，在下一轮中被强烈考虑学习。这一过程迭代多次直至收敛，各分类器加权投票生成最终结果。

随机森林

(Random Forest)是一种基于 bagging 和决策树的集成学习算法。它的核心思想是对多棵决策树进行集成，每棵树的构建都是基于不同的随机子集（如特征选择和数据采样）来构建的，因此每棵树都有着独特的特征和分类能力。随机森林通过对各个子集上的树进行投票来生成最终的分类结果，这样的结果能够降低个别子集上出现的过拟合风险。随机森林不仅可以用于分类，还可以用于回归，它在实际应用和工业界得到了广泛应用，因为它不仅具有良好的鲁棒性、并且能处理高纬度数据和大规模数据集。

聚类

聚类任务的形式描述可以用以下数学公式表达：

给定一个包含 N 个数据点的数据集 D = {x1, x2, …, xN}，其中每个数据点 x 是一个 d 维向量，即 $x\in R^d$。

假设我们需要将这个数据集分成 K 个不同的簇（cluster），其中每个簇表示一个数据的子集，即 $C_1,C_2,...,C_K$。

聚类任务的目标是找到一种划分方式，使得同一簇内的数据点之间的相似度较高，而不同簇之间的相似度较低。一种常用的相似度度量方式是欧氏距离。形式化地，可以定义以下目标函数：

$$\text{minimize}\sum _{k=1}^K\sum _{x_i\in C_k}||x_i-{\mu }_k|{|}^2$$

其中 ${\mu }_k$ 表示第 k 个簇的代表性样本，即该簇所有数据点的平均值。该目标函数表示将每个数据点与其所属簇的代表性样本之间的欧氏距离之和最小化，即最小化簇内距离，最大化簇间距离，从而实现聚类的目的。

DBI是Davies-Bouldin index（戴维斯-博尔丁指数）的缩写，它是一种用于衡量聚类算法效果优劣的指标，其数值越小越好。它通过计算聚类簇间距离和聚类簇内数据散布程度的比率，来评估聚类结果的紧密度和分离度。其公式为$DBI=\frac{1}{k}{\sum }_{i=1}^{k}ma{x}_{j\ne i}(\frac{S_i+S_j}{M_{ij}})$，其中$S_i$为类内样本到质心的平均距离，$M_{ij}$为质心距离。

DI是Dunn index（邓恩指数）的缩写，它也是一种衡量聚类算法性能的指标。与DBI不同的是，DI的数值越大越好。它是通过计算簇内最远两个样本间距离的最小值和簇间质心距离的最大值的比率来评估聚类效果的。其公式为$DI=\frac{mi{n}_{1\le i\le k,1\le j\le k,i\ne j}{d}_{ij}}{ma{x}_{1\le i\le k}{D}_i}$，其中$d_{ij}$表示第$i$个簇内最远两点的距离，$D_i$表示第$i$个簇内所有点之间距离的平均值。

以下是几种常见的聚类算法：

1. K-Means聚类算法

K-Means聚类算法是一种基于质心的聚类方法，它将数据点分成K个簇，每个簇由其重心（centroid）表示。该算法通过迭代更新每个簇的重心，并将每个数据点分配到最近的重心所在的簇中，直到簇的分配不再改变或达到最大迭代次数为止。

2. 层次聚类算法

层次聚类算法是一种基于树形结构的聚类方法，它将数据集中的每个数据点视为一个单独的簇，并逐步合并这些簇，直到所有数据点都在同一个簇中为止。该算法可以分为自下而上的聚合（Agglomerative Clustering）和自上而下的分裂（Divisive Clustering）两种方法。

3. DBSCAN聚类算法

DBSCAN聚类算法是一种基于密度的聚类方法，它通过考虑每个数据点周围的密度来确定簇的形状和大小。具体来说，该算法将密度较大的数据点聚为一簇，并将密度较小的数据点视为噪声点。该算法的主要优点在于它能够处理任意形状的簇，并可以自动识别噪声点。

4. 谱聚类算法

谱聚类算法是一种基于图形论的聚类方法，它将数据集中的每个点视为图中的一个节点，并通过计算每个点与其他点之间的相似度来构建图。然后，该算法将图划分为若干个子图，每个子图表示一个簇。该算法的主要优点在于它能够处理非线性的数据分布，并可以生成任意形状的簇。