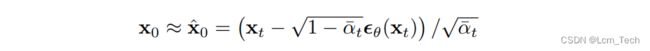【diffusers】(二) scheduler介绍 & 代码解析

1.简介

距离上一次更新已经很久了hhh，刚换了工作，最近才有时间更新博客。

ok接下来我们继续介绍diffusers中的模块，最重要的我觉得一定是scheduler，因为它这里面包含了扩散模型的基本原理，通过对代码的分析我们可以对论文中的公式有着更好的理解，同时scheduler也在DDPM的基础上优化了许多不同的版本，加深对这些scheduler的理解也可以帮助我们在实际选择scheduler时有更好的理论支持。

---

2.scheduler

Diffusion里的scheduler和pytorch里的scheduler完全不同，它的功能是实现逆向扩散，直观上理解的话它就是一个采样器，循环多个step把噪声图像逐渐还原为原始图像。根据采样方式不同，scheduler也有许多版本，包括DDPM，DDIM，DPM++ 2M Karras等。

注意：看下面内容前最好对扩散模型的原理有一定了解，可参考论文2006.11239.pdf (arxiv.org)

---

3.DDPM

 接下来我们先以最基础的DDPM为例，分析diffusers库里的对应代码。代码在

diffusers/src/diffusers/schedulers/scheduling_ddpm.py中，以下是核心部分step函数的代码：

    def step(
        self,
        model_output: torch.FloatTensor,
        timestep: int,
        sample: torch.FloatTensor,
        generator=None,
        return_dict: bool = True,
    ) -> Union[DDPMSchedulerOutput, Tuple]:
        """
        Predict the sample from the previous timestep by reversing the SDE. This function propagates the diffusion
        process from the learned model outputs (most often the predicted noise).

        Args:
            model_output (`torch.FloatTensor`):
                The direct output from learned diffusion model.
            timestep (`float`):
                The current discrete timestep in the diffusion chain.
            sample (`torch.FloatTensor`):
                A current instance of a sample created by the diffusion process.
            generator (`torch.Generator`, *optional*):
                A random number generator.
            return_dict (`bool`, *optional*, defaults to `True`):
                Whether or not to return a [`~schedulers.scheduling_ddpm.DDPMSchedulerOutput`] or `tuple`.

        Returns:
            [`~schedulers.scheduling_ddpm.DDPMSchedulerOutput`] or `tuple`:
                If return_dict is `True`, [`~schedulers.scheduling_ddpm.DDPMSchedulerOutput`] is returned, otherwise a
                tuple is returned where the first element is the sample tensor.

        """
        t = timestep

        prev_t = self.previous_timestep(t)

        if model_output.shape[1] == sample.shape[1] * 2 and self.variance_type in ["learned", "learned_range"]:
            model_output, predicted_variance = torch.split(model_output, sample.shape[1], dim=1)
        else:
            predicted_variance = None

        # 1. compute alphas, betas
        alpha_prod_t = self.alphas_cumprod[t]
        alpha_prod_t_prev = self.alphas_cumprod[prev_t] if prev_t >= 0 else self.one
        beta_prod_t = 1 - alpha_prod_t
        beta_prod_t_prev = 1 - alpha_prod_t_prev
        current_alpha_t = alpha_prod_t / alpha_prod_t_prev
        current_beta_t = 1 - current_alpha_t

        # 2. compute predicted original sample from predicted noise also called
        # "predicted x_0" of formula (15) from https://arxiv.org/pdf/2006.11239.pdf
        if self.config.prediction_type == "epsilon":
            pred_original_sample = (sample - beta_prod_t ** (0.5) * model_output) / alpha_prod_t ** (0.5)
        elif self.config.prediction_type == "sample":
            pred_original_sample = model_output
        elif self.config.prediction_type == "v_prediction":
            pred_original_sample = (alpha_prod_t**0.5) * sample - (beta_prod_t**0.5) * model_output
        else:
            raise ValueError(
                f"prediction_type given as {self.config.prediction_type} must be one of `epsilon`, `sample` or"
                " `v_prediction`  for the DDPMScheduler."
            )

        # 3. Clip or threshold "predicted x_0"
        if self.config.thresholding:
            pred_original_sample = self._threshold_sample(pred_original_sample)
        elif self.config.clip_sample:
            pred_original_sample = pred_original_sample.clamp(
                -self.config.clip_sample_range, self.config.clip_sample_range
            )

        # 4. Compute coefficients for pred_original_sample x_0 and current sample x_t
        # See formula (7) from https://arxiv.org/pdf/2006.11239.pdf
        pred_original_sample_coeff = (alpha_prod_t_prev ** (0.5) * current_beta_t) / beta_prod_t
        current_sample_coeff = current_alpha_t ** (0.5) * beta_prod_t_prev / beta_prod_t

        # 5. Compute predicted previous sample µ_t
        # See formula (7) from https://arxiv.org/pdf/2006.11239.pdf
        pred_prev_sample = pred_original_sample_coeff * pred_original_sample + current_sample_coeff * sample

        # 6. Add noise
        variance = 0
        if t > 0:
            device = model_output.device
            variance_noise = randn_tensor(
                model_output.shape, generator=generator, device=device, dtype=model_output.dtype
            )
            if self.variance_type == "fixed_small_log":
                variance = self._get_variance(t, predicted_variance=predicted_variance) * variance_noise
            elif self.variance_type == "learned_range":
                variance = self._get_variance(t, predicted_variance=predicted_variance)
                variance = torch.exp(0.5 * variance) * variance_noise
            else:
                variance = (self._get_variance(t, predicted_variance=predicted_variance) ** 0.5) * variance_noise

        pred_prev_sample = pred_prev_sample + variance

        if not return_dict:
            return (pred_prev_sample,)

        return DDPMSchedulerOutput(prev_sample=pred_prev_sample, pred_original_sample=pred_original_sample)

大家从注释可以看出个大概，但是代码里面可能包含了一些额外的if判断导致不是很清楚，所以我把其中最关键的几句骨架提取出来。

alpha_prod_t = self.alphas_cumprod[t]
alpha_prod_t_prev = self.alphas_cumprod[prev_t] if prev_t >= 0 else self.one
beta_prod_t = 1 - alpha_prod_t
beta_prod_t_prev = 1 - alpha_prod_t_prev
current_alpha_t = alpha_prod_t / alpha_prod_t_prev
current_beta_t = 1 - current_alpha_t

以上代码作用是计算当前step的alpha和beta的对应参数，以上变量分别对应了论文中的

pred_original_sample = (sample - beta_prod_t ** (0.5) * model_output) / alpha_prod_t ** (0.5)

以上代码根据模型的预测噪声推出原始图像，也就是对应论文中公式（15），其中sample就是，代表当前step的加噪图像，model_output代表模型的预测噪声。

pred_original_sample_coeff = (alpha_prod_t_prev ** (0.5) * current_beta_t) / beta_prod_t
current_sample_coeff = current_alpha_t ** (0.5) * beta_prod_t_prev / beta_prod_t

pred_prev_sample = pred_original_sample_coeff * pred_original_sample + current_sample_coeff * sample

以上代码计算了和的系数，对应公式（7），代表上一步计算的原始图像，代表当前step的加噪图像，代表的是分布的均值，对应着代码中的pred_prev_sample。

pred_prev_sample = pred_prev_sample + variance

最后则是在均值上加上噪声variance。

所以总体而言，整个流程满足公式（6），相当于是在基于和基础上的条件概率，而同时也是求一个分布，其中方差（即噪声）完全由step决定，而均值则由初始图像和当前噪声图像决定，又通过模型预测得到噪声计算得到。

---

4.其他采样器

其实在DDPM中，我们已经得到直接求得，为什么还要不断迭代去求呢？

个人理解有以下几点可能性，可能不正确，欢迎讨论：

1）逆向扩散时的条件是满足马尔可夫链，即逆向噪声和正向噪声一样，也是微小高斯噪声，如果直接预测则不满足微小高斯噪声的条件。

2）不断迭代意味着在加噪图像基础上不断细化，这样可以更好控制生成图像中的像素细节。

3）用来计算的是由通过网络预测得到，这就意味着有着很大的随机性和不稳定性，因此直接用一个由初始随机正态噪声图预测得到的是具有很大不确定性的，用这个去直接计算效果也可想而知。因此不断在上一个step的条件上去细化和加上随机噪声（方差），可以带来更多的稳定性和随机性。

 

当然后续也有很多对DDPM进行改进的，来提高推理时间，包括像DDIM，rectified flow等，这里我们拿DDIM来举例。

DDIM就是针对上述DDPM的缺点，去除了马尔可夫条件的限制，重新推导出逆向扩散方程，在代码scheduling_ddim.py中我们也可以看到对应的修改：

std_dev_t = eta * variance ** (0.5)
pred_sample_direction = (1 - alpha_prod_t_prev - std_dev_t**2) ** (0.5) * pred_epsilon
prev_sample = alpha_prod_t_prev ** (0.5) * pred_original_sample + pred_sample_direction

prev_sample = prev_sample + variance

这样我们就可以每次迭代中跨多个step，从而减少推理迭代次数和时间。

当然除了基于DDIM之外还有很多不同原理的采样器，比如Euler，它是基于ODE的比较基础的采样器，以下是Euler在diffusers库scheduling_euler_discrete.py中的核心代码：

pred_original_sample = sample - sigma_hat * model_output

derivative = (sample - pred_original_sample) / sigma_hat
dt = self.sigmas[self.step_index + 1] - sigma_hat
prev_sample = sample + derivative * dt

从代码中可以看出大概的流程：通过对应step的噪声程度预测初始图像，然后通过微分求得对应的梯度方向，然后再向该方向迈进一定步长。

DPM++则会自适应调整步长，DPM2额外考虑了二阶动量，使得结果更准确，但速度更慢。

如果加了a，则表示每次采样后会加噪声，这样可能会导致最后不收敛，但随机性会更强。

如果加了Karras，则代表使用了特定的Karras噪声step表。

如果加了SDE，则代表使用了Score-based SDE方法，使采样过程更加稳定。

后续会介绍diffusers如何训练及数据准备，包括unconditional、txt2img、controlnet等结构。

---

业务合作/学习交流+v：lizhiTechnology