数据结构和算法——哈希查找冲突处理方法（开放地址法-线性探测、平方探测、双散列探测、再散列，分离链接法）

目录

开放地址法（Open Addressing）

线性探测（Linear Probing）

散列表查找性能分析

平方探测（Quadratic Probing） 

定理

平方探测法的查找与插入

双散列探测法（Double Hashing） 

再散列（Rehashing）

分离链接法（Separate Chaining）

平均查找次数

分离链接法的散列表实现

---

常用处理冲突的思路：

• 换个位置：开放定址法
• 同一位置的冲突对象组织在一起：链地址法

开放地址法（Open Addressing）

一旦产生了冲突（该地址已有其它元素），就按某种规则去寻找另一空地址。

若发生了第次冲突，试探的下一个地址将增加，基本公式是：

的不同决定了不同的解决冲突方案：线性探测、平方探测、双散列。

• 线性探测：
• 平方探测：
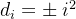
• 双散列：

线性探测（Linear Probing）

线性探测法：以增量序列1,2，......，（TableSize-1）循环试探下一个存储地址。

通俗地来讲，就是当发生冲突时，将关键词+1；检测地址是否为空，如果不为空，就继续+1；如果为空，则表明不冲突了。

【例】设关键词序列为{47,7,29,11,9,84,54,20,30}，散列表表长TableSize = 13（装填因子）;散列函数为：.

用线性探测法处理冲突，列出依次插入后的散列表，并估算查找性能。

为了方便演示，我们先在不考虑冲突的情况下，把所有关键词的散列地址算出来：

关键词（key）	47	7	29	11	9	84	54	20	30
散列地址h（key）	3	7	7	0	9	7	10	9	8

 发现很多地方是冲突的，这次用线性探测法来试着解决冲突。

操作/地址	0	1	2	3	4	5	6	7	8	9	10	11	12	说明
插入47				47										无冲突
插入7				47				7						无冲突
插入29				47				7	29
插入11	11			47				7	29					无冲突
插入9	11			47				7	29	9				无冲突
插入84	11			47				7	29	9	84
插入54	11			47				7	29	9	84	54
插入20	11			47				7	29	9	84	54	20
插入30	11	30		47				7	29	9	84	54	20

最终我们整理得到：

H（key）	0	1	2	3	4	5	6	7	8	9	10	11	12
key	11	30		47				7	29	9	84	54	20
冲突次数	0	6		0				0	1	0	3	1	3

散列表查找性能分析

• 成功平均查找长度(ASLs)
• 不成功平均查找长度(ASLu)

ASLs：查找表中关键词的平均查找比较次数（等于其冲突次数加1） 

即将所有元素的查找次数加起来，最后除以元素的个数

ASLu：不在散列表中的关键词的平均查找次数（不成功）

因为取余数的计算方式，所以所有不在散列表的关键词至多有p-1中情况（表不为空），例如例题中的散列函数，假设其表只有一个元素，那么其不在表中的情况就会有10种，我们一样考虑其需要比较几次。

余数为0的情况，表中位置[0]和[1]都不为空，所以需要比较3次；

余数为1的情况，表中位置[1]不为空，所以需要比较2次；

余数为2的情况，表中位置[2]为空，所以只需要比较1次；

余数为3的情况，表中位置[3]不为空，所以需要比较2次；

......

以此类推。

平方探测（Quadratic Probing） 

平方探测法：以增量序列且循环试探下一个存储地址。

【例】设关键词序列为{47,7,29,11,9,84,54,20,30}，散列表表长TableSize = 11，散列函数为：.用平方探测法处理冲突，列出依次插入后的散列表，并估算ASLs。

关键词（key）	47	7	29	11	9	84	54	20	30
散列地址h（key）	3	7	7	0	9	7	10	9	8

操作/地址	0	1	2	3	4	5	6	7	8	9	10	说明
插入47				47								无冲突
插入7				47				7				无冲突
插入29				47				7	29
插入11	11			47				7	29			无冲突
插入9	11			47				7	29	9		无冲突
插入84	11			47			84	7	29	9
插入54	11			47			84	7	29	9	54	无冲突
插入20	11		20	47			84	7	29	9	54
插入30	11	30	20	47			84	7	29	9	54

注意：用平方探测法，并不是有空间就一定能检测到的。

定理

如果散列表长度TableSize是某个4k+3（k是正整数）形式的素数时，平方探测法就可以探查到整个散列表空间。

平方探测法的查找与插入

#define MAXTABLESIZE 100000 /* 允许开辟的最大散列表长度 */
typedef int ElementType;    /* 关键词类型用整型 */
typedef int Index;          /* 散列地址类型 */
typedef Index Position;     /* 数据所在位置与散列地址是同一类型 */
/* 散列单元状态类型，分别对应：有合法元素、空单元、有已删除元素 */
typedef enum { Legitimate, Empty, Deleted } EntryType;

typedef struct HashEntry Cell; /* 散列表单元类型 */
struct HashEntry{
    ElementType Data; /* 存放元素 */
    EntryType Info;   /* 单元状态 */
};

typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode {   /* 散列表结点定义 */
    int TableSize; /* 表的最大长度 */
    Cell *Cells;   /* 存放散列单元数据的数组 */
};

int NextPrime( int N )
{ /* 返回大于N且不超过MAXTABLESIZE的最小素数 */
    int i, p = (N%2)? N+2 : N+1; /*从大于N的下一个奇数开始 */

    while( p <= MAXTABLESIZE ) {
        for( i=(int)sqrt(p); i>2; i-- )
            if ( !(p%i) ) break; /* p不是素数 */
        if ( i==2 ) break; /* for正常结束，说明p是素数 */
        else  p += 2; /* 否则试探下一个奇数 */
    }
    return p;
}

HashTable CreateTable( int TableSize )
{
    HashTable H;
    int i;

    H = (HashTable)malloc(sizeof(struct TblNode));
    /* 保证散列表最大长度是素数 */
    H->TableSize = NextPrime(TableSize);
    /* 声明单元数组 */
    H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));
    /* 初始化单元状态为“空单元” */
    for( i=0; iTableSize; i++ )
        H->Cells[i].Info = Empty;

    return H;
}

Position Find( HashTable H, ElementType Key )
{
    Position CurrentPos, NewPos;
    int CNum = 0; /* 记录冲突次数 */

    NewPos = CurrentPos = Hash( Key, H->TableSize ); /* 初始散列位置 */
    /* 当该位置的单元非空，并且不是要找的元素时，发生冲突 */
    while( H->Cells[NewPos].Info!=Empty && H->Cells[NewPos].Data!=Key ) {
                                           /* 字符串类型的关键词需要 strcmp 函数!! */
        /* 统计1次冲突，并判断奇偶次 */
        if( ++CNum%2 ){ /* 奇数次冲突 */
            NewPos = CurrentPos + (CNum+1)*(CNum+1)/4; /* 增量为+[(CNum+1)/2]^2 */
            if ( NewPos >= H->TableSize )
                NewPos = NewPos % H->TableSize; /* 调整为合法地址 */
        }
        else { /* 偶数次冲突 */
            NewPos = CurrentPos - CNum*CNum/4; /* 增量为-(CNum/2)^2 */
            while( NewPos < 0 )
                NewPos += H->TableSize; /* 调整为合法地址 */
        }
    }
    return NewPos; /* 此时NewPos或者是Key的位置，或者是一个空单元的位置（表示找不到）*/
}

bool Insert( HashTable H, ElementType Key )
{
    Position Pos = Find( H, Key ); /* 先检查Key是否已经存在 */

    if( H->Cells[Pos].Info != Legitimate ) { /* 如果这个单元没有被占，说明Key可以插入在此 */
        H->Cells[Pos].Info = Legitimate;
        H->Cells[Pos].Data = Key;
        /*字符串类型的关键词需要 strcpy 函数!! */
        return true;
    }
    else {
        printf("键值已存在");
        return false;
    }
}
/*​
源代码来自：https://www.icourse163.org/learn/ZJU-93001?tid=1469696455#/learn/content?type=detail&id=1252518398&cid=1282086737   
​*/

在开放地址散列表中，删除操作要很小心。通常只能“懒惰删除”，即需要增加一个“删除标记（Deleted）”，而并不是真正删除它。以便查找时不会“断链”。其空间可以在下次插入时重用。

双散列探测法（Double Hashing） 

双散列探测法：，是另外一个散列函数，

探测序列成：

对任意的key，！！

探测序列还应该保证所有的散列存储单元都应该能够被探测到。选择以下形式有良好的效果：

其中，p < TableSize，p、TableSize都是素数。

再散列（Rehashing）

• 当散列表元素太多（即装填因子太大）时，查找效率会下降；

比如散列表的大小为11，但此时表中以装填的元素已达到了9个，装填因子就很大了，再进行元素的插入就会很容易发生冲突，实用最大装填因子一般取.

• 当装填因子过大时，解决的方法是加倍扩大散列表，这个过程叫做“再散列（Rehashing）”。

例如散列表的大小为11，就加倍扩大成23（素数），再将所有元素重新插入。

分离链接法（Separate Chaining）

分离链接法：将相应位置上冲突的所有关键词存储在同一个单链表中。

分离链接法在逻辑上比较容易理解，看以下的例题：

【例】设关键字序列为47,7,29,11,16,92,22,8,3,50,37,89,94,21；散列函数取为：;用分离链接法处理冲突。

struct HashTbl
{
    int TableSize;
    List TheLists;
}*H;

平均查找次数

• 表中有9个结点只需1次查找
• 5个结点需要2次查找
• 查找成功的平均查找次数：

分离链接法的散列表实现

#define KEYLENGTH 15                   /* 关键词字符串的最大长度 */
typedef char ElementType[KEYLENGTH+1]; /* 关键词类型用字符串 */
typedef int Index;                     /* 散列地址类型 */
/******** 以下是单链表的定义 ********/
typedef struct LNode *PtrToLNode;
struct LNode {
    ElementType Data;
    PtrToLNode Next;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
/******** 以上是单链表的定义 ********/

typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode {   /* 散列表结点定义 */
    int TableSize; /* 表的最大长度 */
    List Heads;    /* 指向链表头结点的数组 */
};

HashTable CreateTable( int TableSize )
{
    HashTable H;
    int i;

    H = (HashTable)malloc(sizeof(struct TblNode));
    /* 保证散列表最大长度是素数，具体见代码5.3 */
    H->TableSize = NextPrime(TableSize);

    /* 以下分配链表头结点数组 */
    H->Heads = (List)malloc(H->TableSize*sizeof(struct LNode));
    /* 初始化表头结点 */
    for( i=0; iTableSize; i++ ) {
         H->Heads[i].Data[0] = '\0';
         H->Heads[i].Next = NULL;
    }

    return H;
}

Position Find( HashTable H, ElementType Key )
{
    Position P;
    Index Pos;
    
    Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */
    P = H->Heads[Pos].Next; /* 从该链表的第1个结点开始 */
    /* 当未到表尾，并且Key未找到时 */ 
    while( P && strcmp(P->Data, Key) )
        P = P->Next;

    return P; /* 此时P或者指向找到的结点，或者为NULL */
}

bool Insert( HashTable H, ElementType Key )
{
    Position P, NewCell;
    Index Pos;
    
    P = Find( H, Key );
    if ( !P ) { /* 关键词未找到，可以插入 */
        NewCell = (Position)malloc(sizeof(struct LNode));
        strcpy(NewCell->Data, Key);
        Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */
        /* 将NewCell插入为H->Heads[Pos]链表的第1个结点 */
        NewCell->Next = H->Heads[Pos].Next;
        H->Heads[Pos].Next = NewCell; 
        return true;
    }
    else { /* 关键词已存在 */
        printf("键值已存在");
        return false;
    }
}

void DestroyTable( HashTable H )
{
    int i;
    Position P, Tmp;
    
    /* 释放每个链表的结点 */
    for( i=0; iTableSize; i++ ) {
        P = H->Heads[i].Next;
        while( P ) {
            Tmp = P->Next;
            free( P );
            P = Tmp;
        }
    }
    free( H->Heads ); /* 释放头结点数组 */
    free( H );        /* 释放散列表结点 */
}
/*
源代码来自：https://www.icourse163.org/learn/ZJU-93001?tid=1469696455#/learn/content?type=detail&id=1252518398&cid=1282086740
*/

---

end

---

学习自：MOOC数据结构——陈越、何钦铭