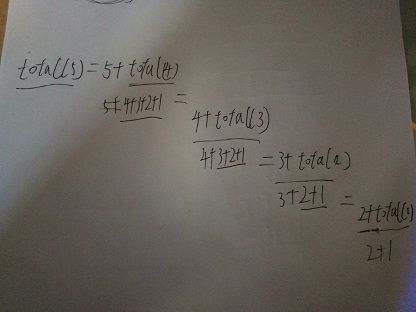暴力递归 转 动态规划
介绍递归和动态规划
暴力递归:
1,把问题转化为规模缩小了的同类问题的子问题
2,有明确的不需要继续进行递归的条件(base case)
3,有当得到了子问题的结果之后的决策过程
4,不记录每一个子问题的解
动态规划
1,从暴力递归中来
2,将每一个子问题的解记录下来,避免重复计算
3,把暴力递归的过程,抽象成了状态表达
4,并且存在化简状态表达,使其更加简洁的可能
什么是暴力递归?
理解下递归
。
首先一个最简单的递归
public static int total(int n){
if(n==1){
return 1;
}
return n+total(n-1);
}计算一个数的累加和
深度分析下这个递归。
比如要求 1到 5 的递归
total(5)
把问题转化为规模缩小了的同类问题的子问题
求 1-5 的累加和。 转化成了 5 + total(4) 5加上 1-4 的累加和
求 1-4 的累加和。 转化成了 4 + total(3) 4加上 1-3 的累加和
求 1-3 的累加和。 转化成了 3 + total(2) 3加上 1-2 的累加和
求 1-2 的累加和。 转化成了 2 + total(1) 2加上 1-1 的累加和
1-1的累加和不需要去求。因为这里是递归的终止条件 base case
此时得到了最后一个子问题的解
应当处理子问题↓↓↓↓↓↓↓↓↓↓↓↓↓
有当得到了子问题的结果之后的决策过程
total(1) = 1、total(2) = 1+2、total(3) = 1+2+3、total(4) = 1+2+3+4、total(5)=1+2+3+4+5
得出最后结果。
得到所有子问题并利用子问题的解去求。之前想要的问题↑↑↑↑↑↑↑↑↑↑↑
public static int total2(int n){
int[] dp = new int[n+1];
//dp[1] 存放的就是 total(1) 的解
//dp[2] 存放的就是 total(2) 的解
//dp[3] 存放的就是 total(3) 的解
//dp[4] 存放的就是 total(4) 的解
//dp[5] 存放的就是 total(5) 的解...
for(int i=1;i倘若使用动态规划的话,就是把每一步的解保存下来。上面的做法有点笨。只是为方便理解
可以通过上一个子问题的解求出下一个问题的
public static int total2(int n){
int[] dp = new int[n+1];
//dp[1] 存放的就是 total(1) 的解
//dp[2] 存放的就是 total(2) 的解
//dp[3] 存放的就是 total(3) 的解
//dp[4] 存放的就是 total(4) 的解
//dp[5] 存放的就是 total(5) 的解...
for(int i=1;i上↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
这样去求累加和只是为了更好的理解动态规划
暴力递归 :不记录每一个子问题的解
动态规划 :记录每一个子问题的解
最短路径问题
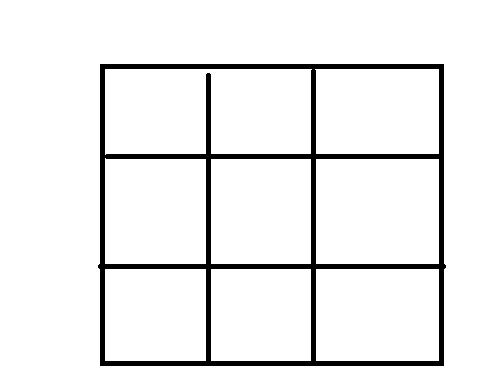
给你一个二维数组,二维数组中的每个数都是正数,要求从左上 角走到右下角,每一步只能向右或者向下。沿途经过的数字要累 加起来。返回最小的路径和
求从左上角走到右下角的最短距离
普通递归去做这道题。
暴力递归:测试所有可能的方案
把每条可以走的路都,走一遍试一下。试试那条路最近。
public static int process1(int[][] arr,int i,int j){
//走到了最后,将最后的值返回,走每一条路都需要加上最后的值
if(i==arr.length-1&&j==arr[0].length-1){
return arr[i][j];
}
//下方走到头了,只能向右走
if(i==arr.length-1){
return arr[i][j] + process1(arr,i,j+1);
}
//右边走到头了,只能向下走
if(j==arr[0].length-1){
return arr[i][j] + process1(arr,i+1,j);
}
//下、右都能走。 看看那条路的代价最小。
return arr[i][j] + Math.min(process1(arr,i+1,j), process1(arr,i,j+1));
}这个递归相当于有分解成了一堆子问题。
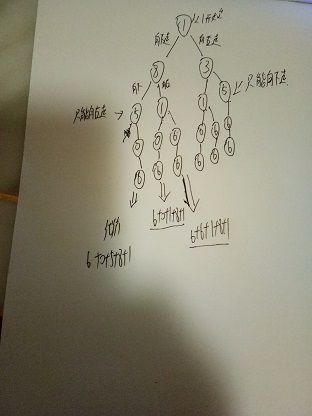
0,0到2,2的最短距离 变成了
1,0 到 2,2 的最短距离
0,1 到 2,2 的最短距离
他们两条路线那个最短距离短,就选择走那条路。
.........................
把每个坐标都理解成一个函数。求他到终点的最短距离
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
首先必须得理解暴力递归。才能写出动态规划。
经过分析。发现好几条路的最短路径已经确定。 可是下一次去求的时候还是会重复计算一次。
这里我们可以用到
记忆化搜索(傻缓存)<这不是完全的动态规划>
把函数的每一个子状态结果存储下来。
每一调用子过程的时候,去cache里面查询一下。
string = 存储坐标
integer = 该坐标到最终距离的最短距离
//记忆化搜索
static HashMap cache = new HashMap();
public static int process2(int[][] matrix,int i,int j){
if(i==matrix.length-1&&j==matrix[0].length-1){
return matrix[i][j];
}
if(i==matrix.length-1){
int right;
String index= i+","+(j+1);
if(!cache.containsKey(index)){
right = process2(matrix,i,j+1);
cache.put(index,right);
}
right = cache.get(index);
return matrix[i][j] + right;
}
if(j==matrix[0].length-1){
int down;
String index= (i+1)+","+j;
if(!cache.containsKey(index)){
down = process2(matrix,i+1,j);
cache.put(index,down);
}
down = cache.get(index);
return matrix[i][j] + down;
}
int right;
int down;
String indexr= i+","+(j+1);
String indexd= (i+1)+","+j;
if(!cache.containsKey(indexr)){
right = process2(matrix,i,j+1);
cache.put(indexr,right);
}
if(!cache.containsKey(indexd)){
down = process2(matrix,i+1,j);
cache.put(indexd,down);
}
return matrix[i][j]+Math.min(cache.get(indexr),cache.get(indexd));
} 动态规划解这道题
把暴力递归的过程,抽象成了状态表达
暴力递归转化成动态规划。完全不需要去考虑题意本身。
只需要关注暴力递归。这一段代码
准备一个数组。他是用来盛放每一个子问题的解的
0,0位置 存放 0,0 到最终2,2的解
0,1位置 存放 0,1 到最终2,2的解
....
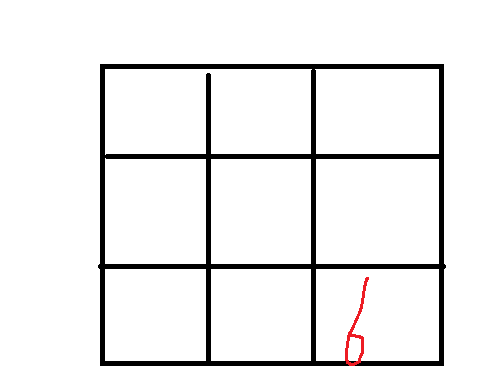
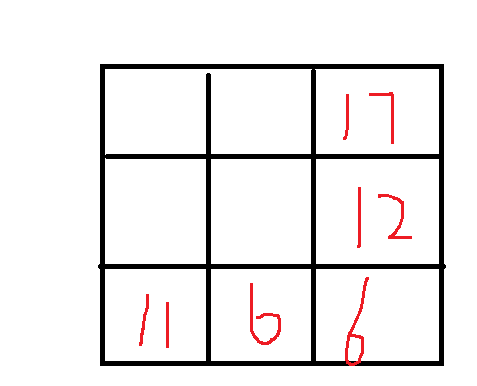
在所有的解 里面 2,2 位置是可以确定的。因为。他就是终止条件
通过 6 可以确定 1,2的最短距离。0,2的最短距离。 因为。他们只能向下走走到 2,2
同理 2,0, 2,1 只能通过 向右走 走到2,2
切记每一个表格位置,存放的是该函数的解
此时。根据递归函数。
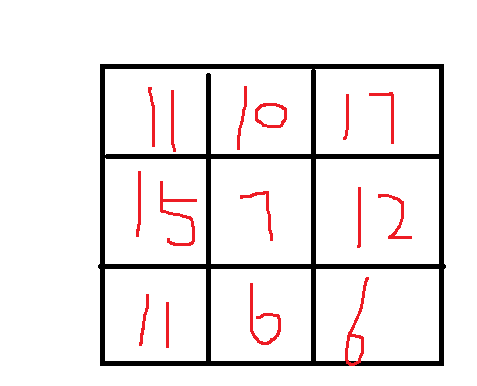
1,1的位置应该 是判断 2,1 1,2 两个解那个小。 自己的路径值加上那个小的解
其他位置同理。可以推理出来
二维数组 0,0 位置就是要求的值。 0,0 到 2,2 的最短距离
这个二维数组里面存放的是 所有 子问题 (函数) 的结果
他是通过递归函数。所有的依赖关系倒着推理出来的。
他和原本的问题没有任何关系。
写出动态规划。需要的就是理解递归。用表格存储下所有子问题的解。
动态规划就是填表格。
//动态规划,就是递归的过程完全理解后,递归出所有位置的解集
public static int process3(int[][] arr){
int row = arr.length-1;
int low = arr[0].length-1;
//构建一个存放所有解的二维数组
int[][] dp = new int[row+1][low+1];
//最后位置的值是可以确定的 因为他是 base case
dp[row][low] = arr[row][low];
for(int i=row-1;i>=0;i--){
dp[i][low] = arr[i][low] + dp[i+1][low];
}
for(int i=low-1;i>=0;i--){
dp[row][i] = arr[row][i] + dp[row][i+1];
}
for(int i=row-1;i>=0;i--){
for(int j=low-1;j>=0;j--){
dp[i][j] = Math.min(arr[i][j]+dp[i+1][j],arr[i][j]+ dp[i][j+1]);
}
}
return dp[0][0];
}将暴力递归改成动态规划的步骤
1、分析可变参数,确定表格空间。(所有解的用数组表示。应该用多大的数组。)
(如果有3个可变参数,就应该用一个3维数组表示。所有的解)
2、确定最终状态(base case)
3、确定初始状态(需要得到的结果)
4、分析一个普遍位置依赖那些位置
5、根据依赖位置顺序。填表格
最短路径全部代码
package basic_class_07;
import java.util.*;
public class Test07 {
public static void main(String[] args) {
// TODO Auto-generated method stub
int[][] a = { { 1, 3, 5 }, { 8, 1, 3 }, { 5, 0, 6} };
System.out.println(process2(a,0,0));
System.out.println(process1(a,0,0));
System.out.println(process3(a));
}
public static int process1(int[][] arr,int i,int j){
//走到了最后,将最后的值返回,走每一条路都需要加上最后的值
if(i==arr.length-1&&j==arr[0].length-1){
return arr[i][j];
}
//下方走到头了,只能向右走
if(i==arr.length-1){
return arr[i][j] + process1(arr,i,j+1);
}
//右边走到头了,只能向下走
if(j==arr[0].length-1){
return arr[i][j] + process1(arr,i+1,j);
}
//下、右都能走。 看看那条路的代价最小。
return arr[i][j] + Math.min(process1(arr,i+1,j), process1(arr,i,j+1));
}
//记忆化搜索
static HashMap cache = new HashMap();
public static int process2(int[][] matrix,int i,int j){
if(i==matrix.length-1&&j==matrix[0].length-1){
return matrix[i][j];
}
if(i==matrix.length-1){
int right;
String index= i+","+(j+1);
if(!cache.containsKey(index)){
right = process2(matrix,i,j+1);
cache.put(index,right);
}
right = cache.get(index);
return matrix[i][j] + right;
}
if(j==matrix[0].length-1){
int down;
String index= (i+1)+","+j;
if(!cache.containsKey(index)){
down = process2(matrix,i+1,j);
cache.put(index,down);
}
down = cache.get(index);
return matrix[i][j] + down;
}
int right;
int down;
String indexr= i+","+(j+1);
String indexd= (i+1)+","+j;
if(!cache.containsKey(indexr)){
right = process2(matrix,i,j+1);
cache.put(indexr,right);
}
if(!cache.containsKey(indexd)){
down = process2(matrix,i+1,j);
cache.put(indexd,down);
}
return matrix[i][j]+Math.min(cache.get(indexr),cache.get(indexd));
}
//动态规划,就是递归的过程完全理解后,递归出所有位置的解集
public static int process3(int[][] arr){
int row = arr.length-1;
int low = arr[0].length-1;
//构建一个存放所有解的二维数组
int[][] dp = new int[row+1][low+1];
//最后位置的值是可以确定的 因为他是 base case
dp[row][low] = arr[row][low];
for(int i=row-1;i>=0;i--){
dp[i][low] = arr[i][low] + dp[i+1][low];
}
for(int i=low-1;i>=0;i--){
dp[row][i] = arr[row][i] + dp[row][i+1];
}
for(int i=row-1;i>=0;i--){
for(int j=low-1;j>=0;j--){
dp[i][j] = Math.min(arr[i][j]+dp[i+1][j],arr[i][j]+ dp[i][j+1]);
}
}
return dp[0][0];
}
}