LeetCode179. 最大数
文章目录
-
-
- 题目描述
- 思路
- 扩展
-
题目描述
给定一组非负整数,重新排列每个数的顺序,使之组成一个最大的整数
思路
排序 + 自定义比较规则
首先考虑最简单的情况,只有2个数,a和b。我们只需要判断把哪个数放在前面就行了。
只要把所有数都按照这样的前后顺序摆好,得到的就是能组成的最大的数。
其实就是排序。但我们需要自定义比较规则。
这样来定义a和b的大小关系:
- 当把
a放在前面,组成的数更大时。我们定义此时a < b - 当把
a放在后面,组成的数更大时。我们定义此时a > b
那么,我们只需要按照上述定义的大小关系,对整个数组进行一次排序,然后依次把每个数取出来,组成的数就是一个最大的数。
那么,这道题的核心点就是,判断a和b之间的大小关系的函数,要怎么写。
我们先把算法的整体框架写出来(手写一个快排)。
代码如下
class Solution {
public String largestNumber(int[] nums) {
quickSort(nums, 0, nums.length - 1);
StringBuilder sb = new StringBuilder();
for (int x : nums) sb.append(x);
// 去除前导0
while (sb.length() > 1 && sb.charAt(0) == '0') sb.deleteCharAt(0);
return sb.toString();
}
private void quickSort(int[] nums, int l, int r) {
if (l >= r) return;
int x = nums[l + r >> 1], i = l - 1, j = r + 1;
while (i < j) {
do i++; while (nums[i] < x); // TODO 这里比较 nums[i] 和 x 的大小, 后续换成自定义的函数
do j--; while (nums[j] > x); // TODO 这里比较 nums[i] 和 x 的大小, 后续换成自定义的函数
if (i < j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
}
quickSort(nums, l, j);
quickSort(nums, j + 1, r);
}
}
然后再来想想,如何实现比较2个数大小的函数
我们从a和b的最高位开始,依次比较每一位上的数字
-
a和b都没有用完所有的位,就比较出了结果假设
a和b,在某一位上的数字不同,则把较大的那个数,放在前面即可比如
9和50,在第一位上发现9 > 5,则要把9放在前面再比如
63723和6381,在第三位上,8 > 7,所以6381放前面需要放在前面的数,在我们的定义中就是较小的数,放在后面的数,是较大的数
-
有一个数用完了所有的位,还未比较出结果,则要换一种方式
a的部分已经用完了,我们要继续比较b超出的部分。怎么比呢?根据上面的图,可以发现。我们设
j为b超出部分的第一位(在这个例子中是第四位,下标为3),设i为b的最高位(下标为0)发现位置
j的数,是9,位置i的数,是6,而9 > 6,则说明b要放在前面,才能使得组成的数更大。所以b应该为较小的数。上面这个例子还可以扩展,若比较
j和i发现相等,怎么办?那就要把j和i各自后移一位,继续比较。这个过程中,注意到j是有可能到达b的末尾的,此时b已经没有数了,此时要换a,来继续比较。比如下面这个例子a=636,b=63663

我们要比较到a的第二位,才能得出结果。需要注意处理这种边界情况。
对于
a超出的情况,同理。我们写出这个比较函数如下
/** * @return 1 when a > b , 0 when a = b, -1 when a < b * **/ private static int compare(int a, int b) { int[] bitsA = new int[10]; // 数最大值为 10^9 , 所以最多10位 int[] bitsB = new int[10]; int lastA = -1, lastB = -1; // 计数 // 取出a和b的每一位 // 用 do while 循环, 以便兼容 a = 0 的情况 do { bitsA[++lastA] = a % 10; a /= 10; } while (a > 0); do { bitsB[++lastB] = b % 10; b /= 10; } while (b > 0); // 从2个数的最高位开始进行比较 // 注意最高位是数组的最后一个位置 int i = lastA, j = lastB; while (i >= 0 && j >= 0) { // 当2个数都没用完所有的位 if (bitsA[i] > bitsB[j]) return -1; // a应该放在前面, 所以a更小, a < b if (bitsA[i] < bitsB[j]) return 1; // b应该放在前面, 所以b更小, a > b i--; j--; } // 有一个数已经用完了所有的位 if (j >= 0) { // 当b还有位置时 int bCur = j, bStart = lastB; // 从当前位置和b的第一个位置开始比较 while (bCur >= 0) { if (bitsB[bCur] > bitsB[bStart]) return 1; // b应该放在前面, b更小 if (bitsB[bCur] < bitsB[bStart]) return -1; // b应该放在后面, b更大 bCur--; bStart--; } // b用完了, 该用a了 int aStart = lastA; while (bStart >= 0) { if (bitsA[aStart] < bitsB[bStart]) return -1; //b应该放后面 if (bitsA[aStart] > bitsB[bStart]) return 1; //b应该放在前面 aStart--; bStart--; } return 0; // 一样大 } else { // 当a还有位置时, 把上面代码复制过来改改即可 int aCur = i, aStart = lastA; while (aCur >= 0) { if (bitsA[aCur] > bitsA[aStart]) return -1; //a放前面 if (bitsA[aCur] < bitsA[aStart]) return 1; // a放后面 aCur--; aStart--; } int bStart = lastB; while (aStart >= 0) { if (bitsB[bStart] < bitsA[aStart]) return 1; // a放后面 if (bitsB[bStart] > bitsA[aStart]) return -1; bStart--; aStart--; } return 0; } }简单测试一下这个函数是否符合我们的预期,用上面提到的几个数据
public static void main(String[] args) { int[][] testCases = new int[][]{{9, 50}, {63723, 6381}, {637, 63798}, {636, 63663}}; for (int[] c : testCases) { int a = c[0]; int b = c[1]; int res = compare(a, b); System.out.printf("a = %d, b = %d ", a, b); if (res > 0) System.out.printf("a > b, res = %d%d\n", b ,a); else if (res < 0) System.out.printf("a < b , res = %d%d\n", a, b); else System.out.printf("a = b, res = %d%d\n", a, b); } }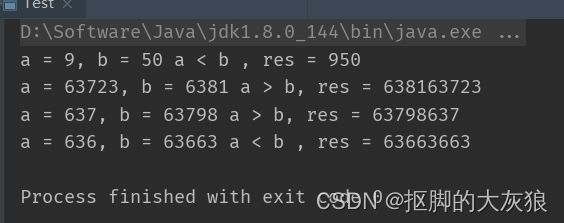
那么应该没问题了,现在把算法框架中比较2个数大小的地方,改成调用这个函数class Solution { public String largestNumber(int[] nums) { quickSort(nums, 0, nums.length - 1); StringBuilder sb = new StringBuilder(); for (int x : nums) sb.append(x); // 去除前导零 while (sb.length() > 1 && sb.charAt(0) == '0') sb.deleteCharAt(0); return sb.toString(); } private void quickSort(int[] nums, int l, int r) { if (l >= r) return; int x = nums[l + r >> 1], i = l - 1, j = r + 1; while (i < j) { do i++; while (compare(nums[i], x) < 0); // 比较大小改为调用自定义的函数 do j--; while (compare(nums[j], x) > 0); // 比较大小改为调用自定义的函数 if (i < j) { int t = nums[i]; nums[i] = nums[j]; nums[j] = t; } } quickSort(nums, l, j); quickSort(nums, j + 1, r); } /** * @return 1 when a > b , 0 when a = b, -1 when a < b * **/ private int compare(int a, int b) { int[] bitsA = new int[10]; // 数最大值为 10^9 , 所以最多10位 int[] bitsB = new int[10]; int lastA = -1, lastB = -1; // 计数 // 取出a和b的每一位 // 用 do while 循环, 以便兼容 a = 0 的情况 do { bitsA[++lastA] = a % 10; a /= 10; } while (a > 0); do { bitsB[++lastB] = b % 10; b /= 10; } while (b > 0); // 从2个数的最高位开始进行比较 // 注意最高位是数组的最后一个位置 int i = lastA, j = lastB; while (i >= 0 && j >= 0) { // 当2个数都没用完所有的位 if (bitsA[i] > bitsB[j]) return -1; // a应该放在前面, 所以a更小, a < b if (bitsA[i] < bitsB[j]) return 1; // b应该放在前面, 所以b更小, a > b i--; j--; } // 有一个数已经用完了所有的位 if (j >= 0) { // 当b还有位置时 int bCur = j, bStart = lastB; // 从当前位置和b的第一个位置开始比较 while (bCur >= 0) { if (bitsB[bCur] > bitsB[bStart]) return 1; // b应该放在前面, b更小 if (bitsB[bCur] < bitsB[bStart]) return -1; // b应该放在后面, b更大 bCur--; bStart--; } // b用完了, 该用a了 int aStart = lastA; while (bStart >= 0) { if (bitsA[aStart] < bitsB[bStart]) return -1; //b应该放后面 if (bitsA[aStart] > bitsB[bStart]) return 1; //b应该放在前面 aStart--; bStart--; } return 0; // 一样大 } else { // 当a还有位置时, 把上面代码复制过来改改即可 int aCur = i, aStart = lastA; while (aCur >= 0) { if (bitsA[aCur] > bitsA[aStart]) return -1; //a放前面 if (bitsA[aCur] < bitsA[aStart]) return 1; // a放后面 aCur--; aStart--; } int bStart = lastB; while (aStart >= 0) { if (bitsB[bStart] < bitsA[aStart]) return 1; // a放后面 if (bitsB[bStart] > bitsA[aStart]) return -1; bStart--; aStart--; } return 0; } } }
扩展
上面这个自定义的比较规则,实现起来有些复杂(因为是纯手工模拟按位比较的过程)。我们可以换个稍微简单点的方式。只要把ab和ba两种组合的数字算出来,再比较一下大小就行啦~下面提供2种实现思路:
- 使用数字计算(需用
long存储,否则会溢出) - 使用字符串,直接比较字符串字典序即可
使用数字计算:
/**
* @return 1 when a > b , 0 when a = b, -1 when a < b
* **/
private int compare(int a, int b) {
long pow10a = 1, pow10b = 1;
int ta = a, tb = b;
do {
pow10a *= 10;
ta /= 10;
} while (ta > 0);
do {
pow10b *= 10;
tb /= 10;
} while (tb > 0);
long ab = a * pow10b + b;
long ba = b * pow10a + a;
if (ab > ba) return -1; // a应该放前面, a小
if (ab < ba) return 1;
return 0;
}
使用字符串
/**
* @return 1 when a > b , 0 when a = b, -1 when a < b
* **/
private int compare(int a, int b) {
String sa = String.valueOf(a);
String sb = String.valueOf(b);
String ab = sa + sb;
String ba = sb + sa;
if (ab.compareTo(ba) > 0) return -1; // ab更大, a放前面, a小
if (ab.compareTo(ba) < 0) return 1;
return 0;
}