【Acwing 第三章——搜索与图论 保姆级教程！！！】Java代码 题号842~848

又来CSDN搬运笔记了，菜鸡一枚，生怕日后复习看不懂代码，所以进行了保姆级注释，希望能帮到在各个点卡住的小伙伴们~
这篇博客包含了Acwing题库 842~848题，java代码实现，是 DFS和BFS的内容。

DFS

排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。按照字典序将所有的排列方法输出。

输入格式：共一行，包含一个整数 n。

输出格式：按字典序输出所有排列方案，每个方案占一行。
数据范围：1≤n≤7

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

思路分析

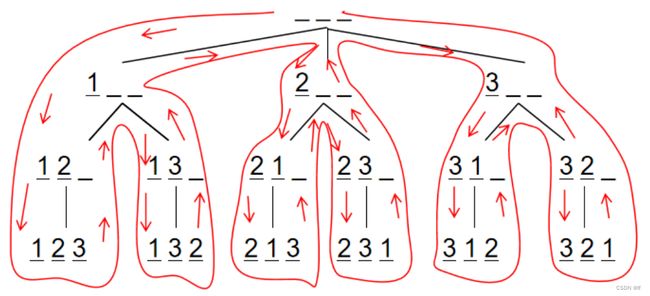
全排列问题，可以看成一个 n 层的树，如图所示。（括号内的字对应的是代码逻辑）

假设 n=3，有 3 个空位，从前往后填数字，每次填一个位置，填的数字不能和前面一样。

最开始的时候，三个空位都是空的：__ __ __

首先填写第一个空位，遍历数字1~n，第一个空位可以填 1，填写后为：1 __ __

填好第一个空位，填第二个空位，这时递归调用dfs，函数体内同样会遍历数字1~n，发现1刚刚已经填过（因为刚刚记录下来到一个静态状态数组），那么第二个空位可以填 2，填写后为：1 2 __

填好第二个空位，填第三个空位，同理递归调用dfs，第三个空位可以填 3，填写后为： 1 2 3

这时候，空位填完（递归层数==n），无法继续填数，所以这是一种方案，输出。

然后往后退一步（退出最后一层的dfs），退到了状态：1 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3 ，没有其他数字可以填（循环1~n已经走到了末尾）。因此再往后退一步（退一层dfs），退到了状态：1 _ _ 。第二个空位上除了填过的 2（刚刚的循环走到2），还可以填 3（dfs退出刚刚第三层时要将3置为可用）。第二个空位上填写 3，填写后为：1 3 _ 。填好第二个空位，填第三个空位，第三个空位可以填 2（dfs退出刚刚第二层时要将2置为可用），填写后为： 1 3 2

这时候，空位填完（递归层数==n），无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：1 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。因此再往后退一步，退到了状态：1 __ _。第二个空位上除了填过的 2，3，没有其他数字可以填（循环走到末尾）。因此再往后退一步，退到了状态： _ _ _。第一个空位上除了填过的 1，还可以填 2。第一个空位上填写 2，填写后为：2 _ _。

之后不再细嗦，和 1 _ _ 的情况一样了。等 2 _ 和 3 _ _ 都填完后退到状态：_ __ __时，第一个空位上除了填过的 1，2，3，没有其他数字可以填。

此时深度优先搜索结束，输出了所有的方案。

算法思路

根据1.1.1的思路，我们可以设计算法如下：

• 用 path 数组保存排列，当排列的长度为 n 时，是一种方案，输出。则每一个分支都有一个path数组，从根部开始记录每一位的数字。
• 用 st 布尔数组记录数字是否用过。因为要在空位上写入数字时，会遍历所有数字，只有没有用过的数字即状态为false的才能填入空位。
• 定义dfs方法，dfs(i) 表示的含义是：在第 i 层，第 i 个空位即 path[i] 处填写数字，然后递归的在下一个位置填写数字。
• 回溯：某一个分支都深度遍历结束了，则一层一层递归退回去把用过的数字置为没用过，开始走另一个分支。

代码实现

PS：debug一步一步看，思路会清晰很多。也可以自己进行手动模拟。（Acwing评论区有大佬画了手动模拟图，但是我还是觉得自己写一遍或者debug比较好，这里就不放图了）

static int n;
static int N = 10;
static boolean[] st = new boolean[N];   //记录数字是否被用过的状态数组
static int[] path = new int[N];    //存储数字排列情况

public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    n = sc.nextInt();
    dfs(0);   //从根部开始dfs
}

public static void dfs(int x){
    if (x == n) {    //如果dfs到了最后一层
        for (int i = 0; i < n; i++)   //就可以输出结果了，即整个path数组
            System.out.print(path[i]+" ");
        System.out.println("");
        return;
    }
    for (int i = 1; i <= n; i++) { //如果dfs还在中间层
        if (!st[i]){   //遍历到一个没有用过的数字
            path[x] = i;   //将该层的空位数字置为这个没用过的数字
            st[i] = true;  //空位填完后，将该数字置为用过了
            dfs(x+1);   //该层填数字的任务完成，继续到下一层
            st[i] = false;  //一直递归调用更深层的dfs，等到执行到这一行的时候，已经是某一个分支都遍历                             结束了（即准备回溯），则一层一层递归退回去把用过的数字置为没用过
        }
    }
}

n皇后问题

​

方法一：按行枚举

思路分析

代码思路

• 函数名：void dfs(int x): 深度优先遍历函数。参数x：从第 x 行开始放棋子，处理第 x 行。

• 递归结束判定：当 x == n的时候，即将处理第n行，说明第 0~n-1行放好棋子了，也就是整个棋盘放好棋子，得到了一种解，也就是递归结束。

• 对于第 x 行，第 i 列能不能放棋子：用数组dg udg col 分别表示：(x, i) 所在的两个对角线和列上是否有皇后。dg 和 udg 的下标表示 第几条对角线，如图：
  
  那么如何将 (x, i) 所在的对角线和dg 和 udg 的下标相映射呢？根据截距公式：
  为了保证 “y - x” 是正数，可以加上一个偏置 n（也可以是2n啥的，能映射过去就行）。（这里的横坐标就是 i （列），纵坐标就是 x（行）） 。因此，有 dg[i + x] 表示 x 行i列处，所在的对角线上有没有Q，udg[ x - i + n]表示 x行 i 列处，所在的反对角线上有没有Q。

• col [i] 表示第 i 列上有没有棋子。如果(x, i) 所在的两个对角线和列上都无皇后即 !col[i] && !dg[i + x] && !udg[n - i + x]为真，则代表 x 行 i 列处可以放棋子。

代码实现

static int n;
static int N = 20;
static boolean[] col=new boolean[N];
static boolean[] dg=new boolean[N];
static boolean[] udg=new boolean[N];
static char[][] g = new char[N][N];    //存储数字排列情况

public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    n = sc.nextInt();
    for (int i = 0; i < n; i++)    //初始化全为.
        for (int j = 0; j < n; j++)
            g[i][j]='.';
    dfs(0);
}

public static void dfs(int x){
    if (x == n) {    //如果dfs到了最后一层
        for (int i = 0; i < n; i ++ )
        {
            for (int j = 0; j < n; j ++ )   //这里不能直接省去循环输出g[i]，因为会输出很多null
                System.out.print(g[i][j]);
            System.out.println();
        }
        System.out.println();
        return;
    }
    for (int i = 0; i < n; i++) { 
        if (!col[i] && !dg[x+i] && !udg[n-x+i]){   //遍历到一个列、主对角线、副对角线都不冲突（没有Q在）的位置i
            g[x][i] = 'Q';
            col[i] = dg[x+i] = udg[ n-x+i ] = true;
            dfs(x+1);
            col[i] = dg[x+i] = udg[ n-x+i ] = false; //递归向上一层时要记得恢复现场
            g[x][i] = '.';
        }
    }
}

方法二：逐个枚举（更好理解，效率更低）

思路

从左到右从上到下逐个枚举，每个位置无外乎两种情况：放或不放。如此就要多加一个防止行冲突的状态数组row

代码实现

static int n;
static int N = 20;
static boolean[] row=new boolean[N];
static boolean[] col=new boolean[N];
static boolean[] dg=new boolean[N];
static boolean[] udg=new boolean[N];
static char[][] g = new char[N][N];    //存储数字排列情况

public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    n = sc.nextInt();
    for (int i = 0; i < n; i++)    //初始化全为.
        for (int j = 0; j < n; j++)
            g[i][j]='.';
    dfs(0,0,0);
}

public static void dfs(int x, int y, int s){   //x表示行，y表示列，s表示放置的皇后个数
    //先对特殊位置进行处理
    if (y==n){  //当枚举到行末尾的时候
        y = 0;
        x++;  //换到下一行
    }
    if (x == n) {    //枚举到最后一行
        if (s == n) {   //皇后也放置了n个，就表示可以输出了
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++)   //注意：这里不能直接省去循环输出g[i]，因为这样会输出很多null
                    System.out.print(g[i][j]);
                System.out.println();
            }
            System.out.println();
        }
        return;
    }

    //开始对每一格进行讨论
    //满足条件则放皇后
    if (!row[x] && !col[y] && !dg[x+y] && !udg[n-y+x]){   //遍历到一个行、列、主对角线、副对角线都不冲突（没有Q在）的位置i
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x+y] = udg[ n-y+x ] = true;
        dfs(x,y+1,s+1);
        row[x] = col[y] = dg[x+y] = udg[ n-y+x ] = false; //递归向上一层时要记得恢复现场
        g[x][y] = '.';
    }
    
    //不放皇后
    dfs(x,y+1,s);  //继续往下一个格子枚举
}

BFS

走迷宫

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。最初，有一个人位于左上角 (1,1)处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。

数据保证 (1,1)处和 (n,m)处的数字为 0，且一定至少存在一条通路。

输入格式：第一行包含两个整数 n和 m。接下来 n 行，每行包含 m个整数（0或1），表示完整的二维数组迷宫。

输出格式：输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围 ：1≤n,m≤100

输入样例：

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：

8

队列相关java代码

本题需要用到队列，队列在java中的相关使用如下：

1. java队列声明

Java 中队列的声明可以使用 Queue 接口，它是一个集合接口，继承自 Collection 接口。Queue 接口有两个实现类：LinkedList 和 PriorityQueue。其中 LinkedList 是一个双向链表，可以用作队列和栈；PriorityQueue 是一个优先队列，可以按照元素的自然顺序或者指定的比较器顺序进行排序。

声明一个 LinkedList 队列的示例代码如下：

//Queue<结点类型> 队列名 = new 队列实现类<>();
Queue<String> queue = new LinkedList<>();

其中String为队列中结点的类型，也可以是自定义class等。

2. Queue的6个方法分类：

压入元素(添加)：add()、offer()
相同：未超出容量，从队尾压入元素，返回压入的那个元素。
区别：在超出容量时，add()方法会对抛出异常，offer()返回false

弹出元素(删除)：remove()、poll()
相同：容量大于0的时候，删除并返回队头被删除的那个元素。
区别：在容量为0的时候，remove()会抛出异常，poll()返回false

获取队头元素(不删除)：element()、peek()
相同：容量大于0的时候，都返回队头元素。但是不删除。
区别：容量为0的时候，element()会抛出异常，peek()返回null。

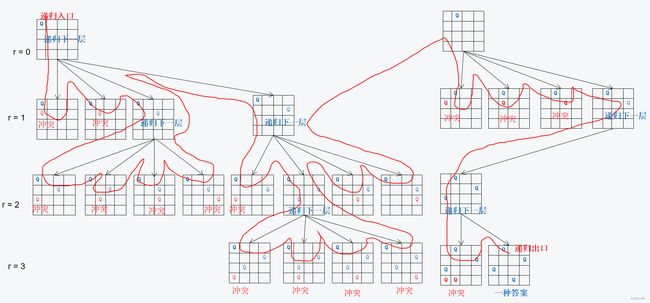
思路分析

本题思路挺简单的，主要是要理解队列在其中的用法。用 map 存储地图，d 存储起点到其他各个点所走过的距离。从起点开始广度优先遍历地图。当地图遍历完，就求出了起点到各个点的距离，输出d [n-1] [m-1]即可。

代码逻辑

为什么想到用队列？

通过2.1.2的分析，每走一步就有一个新结点，这个结点刚好是下一步的起点（即看它周围哪能走）。既是所求的结点，又是之后需要拿出来用的点，而且先求的要先用，刚好符合队列的用法（自己思考一下）。

刚开始，在队列中新建一个结点，之后开始遍历上下左右四个位置。方法如下：

向上：(x,y) + (0,1) ； 向下：(x,y) + (0,-1) ；向左：(x,y) + (-1,0) ；向右：(x,y) + (1,0) ；

具体方法：定义 dx = { 1, -1, 0, 0 }; dy = { 0, 0, 1, -1 }，令 x+dx[i]、y+dy[i] 表示x、y坐标的移动。

遍历中若找到合理位置——未到终点、还在map中、不是墙、还未走过（判断条件），则新建结点插入队尾，并将该合理位置的计数+1。

之后循环在队头中取出结点，重复上述步骤，直到走到终点，打印出计数，就是我们要的答案。

代码实现

//844.走迷宫
import java.util.LinkedList;
import java.util.Queue;
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class maze {
    //通过循环来进行组合,分别表示向左向右向上向下
    static int[] dx = { 1, -1, 0, 0 };
    static int[] dy = { 0, 0, 1, -1 };
    static int[][] map = null;//定义一个二维数组用来存图中的每一个坐标是可以走的0，还是不可以走的墙1
    static int[][] d = null;//定义一个二维数组用来存储图上(x,y)位置的已移动次数
    static int n, m;

    public static void main(String[] args) throws Exception {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        String str[] = bf.readLine().split(" ");
        n = Integer.parseInt(str[0]);
        m = Integer.parseInt(str[1]);
        map = new int[n][m];
        d = new int[n][m];
        for (int i = 0; i < n; i++) {
            String s[] = bf.readLine().split(" ");
            for (int j = 0; j < m; j++) {
                map[i][j] = Integer.parseInt(s[j]);
            }
        }
        System.out.println(bfs());
    }

    public static int bfs() {
        //定义一个队列
        Queue<point> q = new LinkedList<>();
        //offer:添加一个元素并返回true，如果队列已满，则返回false
        q.offer(new point(0, 0));
        while (!q.isEmpty()) {
            //poll：拿出队列头部的元素（即上一步走到的点），如果队列为空，则返回null
            point point = q.poll();
            //如果遍历到了(m-1,n-1)——走到终点
            if (point.x == n - 1 && point.y == m - 1) {
                break;
            }
            //如果还未遍历到了(m-1,n-1)
            //用坐标表示向上下左右
            //向上：x-1,y 向下：x+1,y 向左：x,y-1 向右：x,y+1
            //用循环来表示分别向上向下向左向右
            for (int i = 0; i < 4; i++) {
                int x = point.x + dx[i];
                int y = point.y + dy[i];
                //如果(x-1,y-1)这个坐标还未到终点，并且还在所给的map中，并且不是墙，并且还未走过
                if (x >= 0 && x < n && y >= 0 && y<m && map[x][y] == 0 && d[x][y] == 0){
                    //满足以上要求，就更新一下d，即累加移动次数到新的这个点上，向前走一步
                    //offer:添加一个元素并返回true，如果队列已满，则返回false
                    q.offer(new point(x, y));
                    //记录移动次数
                    d[x][y] = d[point.x][point.y] + 1;
                }
            }
        }
        //最后把右下角的点中存储的移动次数输出来就可以了
        return d[n - 1][m - 1];
    }
}
//定义point类，包含属性行x，列y
class point {
    int x;
    int y;

    public point(int x, int y) {
        this.x = x;
        this.y = y;
    }
}

邻接表表示的模板代码

1. 首先弄清楚几个变量的含义：

N ： 节点数量 M：边的数量 i : 节点的下标索引 idx ： 边的下标索引

h[N] : 第 i 个节点的第一条边的 idx ne[M] : 与 第 idx 条边 同起点 的 下一条边 的 idx

e[M] : 第idx 条边的终点的编号

2. 然后结合代码模版理解定义

变量初始化定义：

int h[N], e[M], ne[M], idx;

当加入一条边的时候：（如2——> 3）

我们需要：1.记录该边的终点（代码第一行）；2.插入到起点所在的链表的头部，包括前接起点（代码第三行，图中1）和后接本来的起点第一个结点（代码第二行，图中2）

public static void add(int a,int b){
     e[idx] = b;      // 记录 加入的边 的终点
     ne[idx] = h[a]; // h[a] 表示 节点 a 为起点的第一条边的下标，ne[idx] = h[a] 表示把 h[a] 这条边接在了 idx 这条边的后面，其实也就是把 a 节点的整条链表 接在了 idx 这条边 后面；目的就是为了下一步 把 idx 这条边 当成 a 节点的单链表的 第一条边，完成把最新的一条边插入到 链表头的操作；
     h[a] = idx++; // a节点开头的第一条边置为当前边，并且将边的下标自增
}

树与图的深度优先遍历

dfs框架

//树和图的dfs框架
void dfs(int u){   //从编号为u的点开始dfs
    st[u] = true;
    //从点u的第一条边开始遍历，循环体内递归dfs，即顺着这条边往下遍历到底
    for (int i = h[u]; i != -1 ; i = ne[i]) {
        int j = e[i];  //取出该边的终点，即下一轮dfs的起点
        if (!st[j])
            dfs(j);
    }
}

树的重心

给定一颗包含 n 个结点（编号 1∼n）和 n−1条无向边的树。找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式：第一行包含整数 n，表示树的结点数。接下来 n−1 行，每行包含两个整数 a和 b，表示点 a 和点 b之间存在一条边。

输出格式：输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围：1≤n≤10^5

输入样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4

思路分析

首先，要找到一个树的重心，我们需要依次枚举将各点删除后，剩余每个连通块中节点数的最大值。

举例如图所示的树：

比如我们将 1 号根节点删掉，剩下了 3 个连通块，其中连通块中节点数最大值为 4（包含4、3、6、9六个节点），如图所示：

比如我们将 4 号节点删去，也剩余 3 个连通块，其中连通块中节点数最大值为 5（包含1、2、7、8、5五个节点）：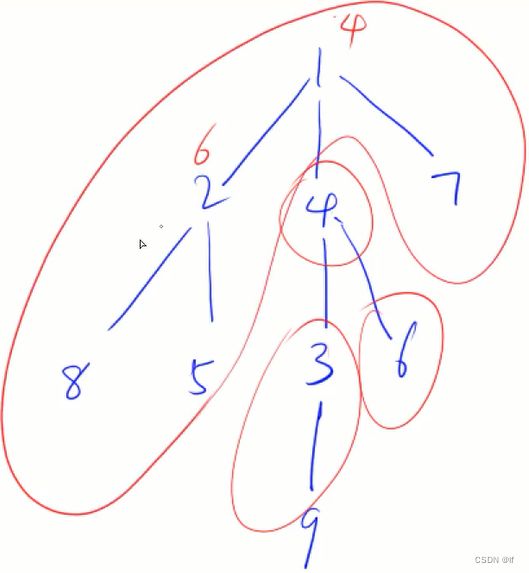

我们的目标是求出并输出“最小的最大值”，经过树中所有点的枚举，我们可以得出最优解就是 4（即第一种情况），即 将树中的重心删除后，剩余各连通块中点数最大值为 4。

具体实现思路

只要对于树中每个节点都能求出 “把这个点删除后，剩余各连通块点数的最大值”，之后在所有值中求得最小值，就是我们目标的答案。那么如何求得将每个点删去后的剩余各连通块的点数呢？答案：运用树的深度优先遍历。

以上面最后一张图的情况为例。删去 4 之后，剩余 3 个连通块：{3，9}、{6}、{1，2，7，8，5}。步骤如下：

1. 通过 dfs 求出 结点4 的子树——也就是将来的连通块成员 的大小。如图子树为 {3，9}、{6}，大小分别为2和1。并且要定义一个变量 sum_u 记录被删结点 4 的这棵树的大小，在计算子树大小完，累加上去；
2. 在求完作为子树部分的连通块后，还剩被删结点 4 的父辈部分的连通块。这部分大小就 = 总节点数 n - sum_u
3. 这样的话，所有连通块的大小都能算出来。可得：在 dfs 的过程当中，递归每一个节点的时候，我们都可以计算出 将这个点删去之后，其余各个连通块的大小。那么在删除某个结点的情况下 不断更新连通块的最大值，继而在全局 不断更新连通块的最大值的最小值就是我们要的答案。（有点绕，具体看代码）

代码实现

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.lang.reflect.Array;
import java.util.Arrays;

//846.树的重心
public class Tree_Graph {
    static int N = 100010, M = N*2;   //节点数量和边的数量
    // 一个节点数为 N 的树的最大边数是 N-1，无向图要存两条，则边数最多是 2*(N-1)
    static int h[] = new int[N];  //存储各节点的第一条边的下标索引
    static int e[] = new int[M];   //第idx条边的终点的编号
    static int ne[] = new int[M];   //与 第 idx 条边 同起点 的 下一条边 的 idx
    static int idx;    //边的下标索引
    static boolean st[] = new boolean[N];  //记录该点是否被访问过
    static int ans;  //我们要求的 删去重心后 所有连通块中 点数最大的块 的值
    static int n;   //输入的树的节点数

    //邻接表添加新边的方法
    public static void add(int a,int b){
        e[idx] = b;      // 记录 加入的边 的终点
        ne[idx] = h[a]; // h[a] 表示 节点 a 为起点的第一条边的下标，ne[idx] = h[a] 表示把 h[a] 这条边接在了 idx 这条边的后面，其实也就是把 a 节点的整条链表 接在了 idx 这条边 后面；目的就是为了下一步 把 idx 这条边 当成 a 节点的单链表的 第一条边，完成把最新的一条边插入到 链表头的操作；
        h[a] = idx++; // a节点开头的第一条边置为当前边，并且将边的下标自增
    }

    public static int dfs(int u){   //返回以编号为u的点为根节点的树的所有节点数量和（包含u）
        st[u] = true;
        int sum_u = 1;   //记录这个要返回的值，即树u的大小，初始化为1，即包含节点u
        int biggestSum = 0;  //删除树中某个节点后 最大连通块的节点数

        //从点u的第一条边开始遍历，循环体内递归dfs，即顺着这条边往下遍历到底之后再换一条边
        for (int i = h[u]; i != -1 ; i = ne[i]) {
            int j = e[i];  //取出该边的终点，即下一轮dfs的起点
            if (!st[j]){
                int sum_j = dfs(j);  //子树 j 的大小
                biggestSum = Math.max(biggestSum,sum_j);   //子树j是删除节点u后 其中一个连通块，取max更新最大连通子图的节点数
                sum_u += sum_j;  //树u的节点数要累加上子树j的节点数
            }
        }
        biggestSum = Math.max(biggestSum, n - sum_u);   //前述循环结束则找到了 u的子树中最大的连通块，和u的父辈部分的连通块取最大值
        ans = Math.min(ans, biggestSum);
        return sum_u;
    }

    public static void main(String[] args) throws Exception{
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(bf.readLine());
        ans = n;
        Arrays.fill(h,-1);   //将h数组初始化全为-1(满足dfs的for循环退出条件)
        for (int i = 0; i < n-1; i++) {
            String s[] = bf.readLine().split(" ");
            int a = Integer.parseInt(s[0]);
            int b = Integer.parseInt(s[1]);
            add(a,b);
            add(b,a);
        }
        dfs(1);
        System.out.println(ans);
    }
}

树与图的广度优先遍历

图中点的层次

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环。所有边的长度都是 1，点的编号为 1∼n。

请你求出 1 号点到 n 号点的最短距离，如果从 1号点无法走到 n 号点，输出 −1。

输入格式：第一行包含两个整数 n 和 m。接下来 m 行，每行包含两个整数 a 和 b，表示存在一条从 a 走到 b 的长度为 1 的边。

输出格式：输出一个整数，表示 1 号点到 n 号点的最短距离。

数据范围：1 ≤ n, m ≤ 10^5

输入样例：

4 5
1 2
2 3
3 4
1 3
1 4

输出样例：

1

BFS框架

将初始元素入队；进入 while 循环，取出队头元素 t，因为是 bfs，则要拓展 t 的下一个节点的所有邻节点——for循环遍历找出未遍历过的邻节点 x，将其插入队尾，并将走到 x 的累积步数 +1。

BFS部分代码实现

public static int bfs() {
    //定义一个队列
    Queue<Integer> q = new LinkedList<>();
    //offer:添加一个元素并返回true，如果队列已满，则返回false
    q.offer(1);
    d[1] = 0;   //1号结点是起点，步数为0
    while (!q.isEmpty()) {
        //poll：拿出队列头部的元素（即上一步走到的点），如果队列为空，则返回null
        int t = q.poll();
        for (int i = h[t]; i != -1 ; i = ne[i]) {   //遍历所有t的下一个结点（即按bfs的规则的同一层的所有节点）
            int j = e[i];  //取出该边的终点
            if (d[j] == -1){   //若这个点没被走到过
                q.offer(j);   //将该点入队并累加步数
                d[j] = d[t] + 1; 
            }
        }
    }
    return d[n];   //返回走到编号为n的点时的累加步数，即我们要求的最短路
}

代码实现

本题代码相当于是 4.2 树的重心和 2.1 走迷宫的结合，没有什么难度。

//847.图中点的层次
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Tree_Graph {
    static int N = 100010;
    static int h[] = new int[N];  //存储各节点的第一条边的下标索引
    static int e[] = new int[N];   //第idx条边的终点的编号
    static int ne[] = new int[N];   //与 第 idx 条边 同起点 的 下一条边 的 idx
    static int idx;    //边的下标索引
    static int d[] = new int[N];   //保存某节点的已走步数
    static int n, m;

    public static void main(String[] args) throws Exception {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        String str[] = bf.readLine().split(" ");
        n = Integer.parseInt(str[0]);
        m = Integer.parseInt(str[1]);
        Arrays.fill(h,-1);   //将h数组初始化全为-1(满足dfs的for循环退出条件)
        Arrays.fill(d,-1);
        for (int i = 0; i < m; i++) {
            String s[] = bf.readLine().split(" ");
            int a = Integer.parseInt(s[0]);
            int b = Integer.parseInt(s[1]);
            add(a,b);
        }
        System.out.println(bfs());
    }

    //邻接表添加新边的方法
    public static void add(int a,int b){
        e[idx] = b;      // 记录 加入的边 的终点
        ne[idx] = h[a]; // h[a] 表示 节点 a 为起点的第一条边的下标，ne[idx] = h[a] 表示把 h[a] 这条边接在了 idx 这条边的后面，其实也就是把 a 节点的整条链表 接在了 idx 这条边 后面；目的就是为了下一步 把 idx 这条边 当成 a 节点的单链表的 第一条边，完成把最新的一条边插入到 链表头的操作；
        h[a] = idx++; // a节点开头的第一条边置为当前边，并且将边的下标自增
    }

    public static int bfs() {
        //定义一个队列
        Queue<Integer> q = new LinkedList<>();
        //offer:添加一个元素并返回true，如果队列已满，则返回false
        q.offer(1);
        d[1] = 0;   //1号结点是起点，步数为0
        while (!q.isEmpty()) {
            //poll：拿出队列头部的元素（即上一步走到的点），如果队列为空，则返回null
            int t = q.poll();
            for (int i = h[t]; i != -1 ; i = ne[i]) {   //遍历所有t的下一个结点（即按bfs的规则的同一层的所有节点）
                int j = e[i];  //取出该边的终点
                if (d[j] == -1){   //若这个点没被走到过
                    q.offer(j);   //将该点入队并累加步数
                    d[j] = d[t] + 1;
                }
            }
        }
        return d[n];   //返回走到编号为n的点时的累加步数，即我们要求的最短路
    }
}

拓扑排序

有向图的拓扑序列

给定一个 n 个点 m 条边的有向图，点的编号是 1 到 n，图中可能存在重边和自环。请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。

输入格式：第一行包含两个整数 n 和 m。接下来 m 行，每行包含两个整数 x 和 y，表示存在一条有向边 (x,y)。

输出格式：共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。否则输出 −1。

数据范围：1 ≤ n, m ≤ 10^5

输入样例：

3 3
1 2
2 3
1 3

输出样例：

1 2 3

思路分析

一个有向无环图，一定存在一个入度为0 的点（证明略）。核心代码就是按照图示逻辑编写的拓扑排序的方法，其他和前一题都一样。注意，这里要多加一个辅助数组res用来记录拓扑序列。因为对于 BFS，用C/C++来写是用数组模拟队列，那么人家有指针，意味着即使出队操作，实际上元素也还是在队里的只是指针后移而已。而你java/python没有指针，也就是说，出队之后这个队列就没有原来这个元素了，因此要额外加一个数组来记录出队元素以及记录该数组下标的cnt。

代码实现

//848.有向图的拓扑序列
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Topsort {
    static int N = 100010;
    static int h[] = new int[N];  //存储各节点的第一条边的下标索引
    static int e[] = new int[N];   //第idx条边的终点的编号
    static int ne[] = new int[N];   //与 第 idx 条边 同起点 的 下一条边 的 idx
    static int idx;    //边的下标索引
    static int d[] = new int[N];   //保存某节点的入度
    static int n, m;
    static int res[] = new int[N];  //存储拓扑序列

    public static void main(String[] args) throws Exception {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        String str[] = bf.readLine().split(" ");
        n = Integer.parseInt(str[0]);
        m = Integer.parseInt(str[1]);
        Arrays.fill(h,-1);   //将h数组初始化全为-1(满足dfs的for循环退出条件)
        for (int i = 0; i < m; i++) {
            String s[] = bf.readLine().split(" ");
            int a = Integer.parseInt(s[0]);
            int b = Integer.parseInt(s[1]);
            add(a,b);
            d[b]++;
        }
        if (topsort())   //如果存在拓扑序列
            for (int i = 0; i < n; i++)
                System.out.print(res[i] + " ");
        else
            System.out.print(-1);
    }

    //邻接表添加新边的方法
    public static void add(int a,int b){
        e[idx] = b;      // 记录 加入的边 的终点
        ne[idx] = h[a]; // h[a] 表示 节点 a 为起点的第一条边的下标，ne[idx] = h[a] 表示把 h[a] 这条边接在了 idx 这条边的后面，其实也就是把 a 节点的整条链表 接在了 idx 这条边 后面；目的就是为了下一步 把 idx 这条边 当成 a 节点的单链表的 第一条边，完成把最新的一条边插入到 链表头的操作；
        h[a] = idx++; // a节点开头的第一条边置为当前边，并且将边的下标自增
    }

    public static boolean topsort() {   //存在拓扑序列返回true否则false
        Queue<Integer> q = new LinkedList<>();  //定义一个队列
        int cnt = 0;   //记录res的下标
        for (int i = 1; i <= n; i++)   //先将所有入度为0的点入队并记录到拓扑序列中
            if (d[i] == 0){
                res[cnt++] = i;
                q.offer(i);
            }

        while (!q.isEmpty()) {
            int t = q.poll();
            for (int i = h[t]; i != -1 ; i = ne[i]) {   //遍历所有t的下一个结点（即按bfs的规则的同一层的所有节点）
                int j = e[i];
                d[j]--;
                if (d[j] == 0){
                    res[cnt++] = j;
                    q.offer(j);   
                }
            }
        }
        return cnt == n;   //返回走到编号为n的点时的累加步数，即我们要求的最短路
    }
}