Unnoticeable Backdoor Attacks on Graph Neural Networks总结笔记
UGBA
- 发表期刊: ArXiv 2023
- 问题:图的后门攻击需要大量的攻击预算才能进行有效的后门攻击,而且注入的触发器可以很容易被检测和修剪。
- 基本思想:通过攻击预算的约束生成触发器过程,增加后门攻击的隐蔽性,部署自适应触发器。
- 技术路线:提出UGBA(Unnoticeable Graph Backdoor Attack),一种新的有毒节点选择算法,在关键的代表性节点上附加触发器。获取代表性节点的方法:使用节点标签训练GCN编码器,获得属性和结构信息的表示,对于每个类,可以在学习到的表示上使用聚类算法选择具有代表性的节点。自适应触发器生成器将目标节点的节点特征作为输入。
图后门攻击大多数需要为每个目标节点计算添加/删除的边,在大型数据上产生高额的计算时间和空间开销。同时,在应用中修改节点的属性及其相关链接是不切实际的。
基于子图触发器注入的后门攻击(优点)从以下三个方面解决了上述问题。
-
对于预定义好的触发器,注入到目标图中(即使是大型图)的计算代价很小。当触发器生成器是自适应的时,优化触发器生成也只需要被毒害样本的梯度信息。
-
当后门被注入目标GNN中,在新节点的预测结果很容易被附加的触发器掌控,而不需要额外的图攻击优化过程。使得攻击变得更便利。
-
相较于修改已有节点之间的边,通过后门攻击注入触发器和恶意标签更容易也更切实际。
已有的子图后门攻击的缺陷:
-
使用随机生成的子图触发器,在大型图中需要较大的攻击预算,这增加了被检测到的风险。
-
子图触发器不具有与原图相同的同质性,在真实世界的图中更相似的节点倾向于相互链接,而触发器中不能够保证高相似度分数高的节点相互连接这一性质,使得触发器容易被识别并破坏。
生成触发器和约束攻击预算上实现不可察觉的图后门攻击
投毒攻击:在训练GNN之前对训练图进行扰动,使得GNN在测试图上的预测性能下降。如Nettack攻击。
逃逸攻击:在测试阶段加入扰动,此时GNN模型已被训练好且不能被攻击者修改。
UGBA与其他攻击的两点本质的不同(创新点):
-
自适应产生有效的子图触发器,且能够绕过通过相连节点特征相似度来检测潜在触发器的防御方法。
-
基于聚类算法选择节点,进一步减少攻击预算。
半监督节点分类任务
-
V L ⊆ V V_{L} \subseteq V VL⊆V是有标签的训练集
-
对于测试集 V T V_{T} VT有 V T ∩ V = ∅ V_{T} \cap V = \emptyset VT∩V=∅
图后门攻击预备知识
-
攻击者目标:附有触发器的节点分类为攻击者指定目标,同时其他干净节点的GNN分类结果不变。
-
攻击者知识:训练数据可知,目标模型结构不可知
-
攻击者能力:训练前将预算内的触发器和目标标签的扰动添加到毒害图中;推理阶段,可以将触发器附加到目标测试节点。
-
攻击:将触发器 g g g附在 V P ⊆ V V_{P} \subseteq V VP⊆V中的毒害节点上,并将 V P V_{P} VP中的节点标签改为目标标签 y t y_{t} yt,$ V_{P}$随机选择。
通过实验表明:
-
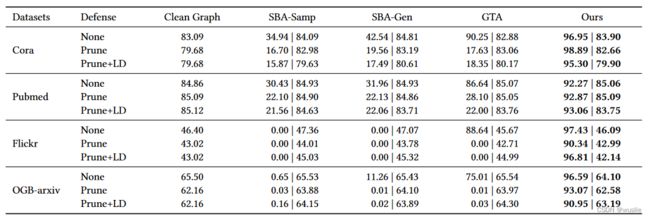
SBA-Samp、SBA-Gen、GTA在攻击预算低(中毒节点数量少)的的情况下,攻击成功率很低。
SBA-Samp、SBA-Gen:使用手工设计的触发器,效果不佳。
GTA:学习样本特有的触发器,但中毒节点随机选取,没用利用好攻击预算。
-
Prune、Prune+LD算法可以成功防御住SBA-Samp、SBA-Gen、GTA的攻击,且不影响干净节点的分类准确率。
Prune:裁剪余弦相似度较低的节点之间的边
Prune+LD:还忽略通过不相似边连接的节点的标签
触发器不可察觉性限制
- 获得与目标节点(毒害节点)相似的自适应触发器,且触发器内的边也要连接相似的顶点。令 E B i \mathcal{E}_{B}^{i} EBi 为触发器内部的边以及连接触发器 g i g_{i} gi与节点 v i v_{i} vi 之间的边。不可察觉的约束可形式化为:
min ( u , v ) ∈ E B i sim ( u , v ) ≥ T (1) \min _{(u, v) \in \mathcal{E}_{B}^{i}} \operatorname{sim}(u, v) \geq T \tag{1} (u,v)∈EBiminsim(u,v)≥T(1)
其中, s i m sim sim是节点特征之间的预先相似度, T T T 为一个相对较高的阈值(根据数据集进行调整)。
攻击形式化
- 干净节点的预测表示为 f θ ( G C i ) f_{\theta}(\mathcal{G}_{C}^{i}) fθ(GCi) ,其中 G C i \mathcal{G}_{C}^{i} GCi 表示节点 v i v_{i} vi 的干净计算图;节点 v i v_{i} vi 附上了触发器 g i g_{i} gi 之后,预测结果表示为 f a ( θ ( G C i , g i ) ) f_{a(\theta}(\mathcal{G}_{C}^{i},g_{i})) fa(θ(GCi,gi)) ,其中 a ( ⋅ ) a(\cdot) a(⋅) 表示为触发器附加(注入)操作。攻击者目标公式化为:
min V P , θ g ∑ v i ∈ V U l ( f θ ∗ ( a ( G C i , g i ) ) , y t ) s.t. θ ∗ = arg min θ ∑ v i ∈ V L l ( f θ ( G C i ) , y i ) + ∑ v i ∈ V P l ( f θ ( a ( G C i , g i ) ) , y t ) , ∀ v i ∈ V P ∪ V T , g i meets Eq.(1) and ∣ g i ∣ < Δ g , ∣ V P ∣ ≤ Δ P (2) \begin{array}{l} \min _{\mathcal{V}_{P}, \theta_{g}} \sum_{v_{i} \in \mathcal{V}_{U}} l\left(f_{\theta^{*}}\left(a\left(\mathcal{G}_{C}^{i}, g_{i}\right)\right), y_{t}\right) \\ \text { s.t. } \theta^{*}=\underset{\theta}{\arg \min } \sum_{v_{i} \in \mathcal{V}_{L}} l\left(f_{\theta}\left(\mathcal{G}_{C}^{i}\right), y_{i}\right)+\sum_{v_{i} \in \mathcal{V}_{P}} l\left(f_{\theta}\left(a\left(\mathcal{G}_{C}^{i}, g_{i}\right)\right), y_{t}\right), \\ \quad \forall v_{i} \in \mathcal{V}_{P} \cup \mathcal{V}_{T}, g_{i} \text { meets Eq.(1) and }\left|g_{i}\right|<\Delta_{g}, \quad\left|\mathcal{V}_{P}\right |\leq \Delta_{P} \end{array} \tag{2} minVP,θg∑vi∈VUl(fθ∗(a(GCi,gi)),yt) s.t. θ∗=θargmin∑vi∈VLl(fθ(GCi),yi)+∑vi∈VPl(fθ(a(GCi,gi)),yt),∀vi∈VP∪VT,gi meets Eq.(1) and ∣gi∣<Δg,∣VP∣≤ΔP(2)
其中, V U \mathcal{V}_{U} VU 是 V \ V T \mathcal{V} \backslash \mathcal{V}_{T} V\VT ,以确保攻击可以有效的针对各种类型的目标节点, l ( ⋅ ) l(\cdot) l(⋅)是交叉熵损失函数。
攻击目标
-
如何选择对后面攻击最有用的中毒节点(节点选择器 f P f_{P} fP )。
-
用节点标签训练一个GCN编码器,同时捕获属性和结构信息的表示。对每个类,在学习到的表示上使用聚类算法来选择具有代表性的节点。
-
通过评分规则 m ( v i ) = ∣ ∣ h i k − h c k ∣ ∣ 2 + λ ⋅ d e g ( v i k ) m(v_{i})=||h_{i}^{k}-h_{c}^{k}||_{2}+\lambda\cdot deg(v_{i}^{k}) m(vi)=∣∣hik−hck∣∣2+λ⋅deg(vik) 计算了节点 v i k v_{i}^{k} vik 属于第 k k k 类的得分,该规则来衡量了特征的表示性和对预测表现的负影响性,其中 h c k h_{c}^{k} hck 表示第 k k k 个类的中心。
-
选择前 n n n 个最高分的满足预算的节点。
-
-
如何学习自适应触发器生成器( f g f_{g} fg ),获得满足不可察觉约束的触发器,并在后门攻击中保持较高的成功率(欺骗代理GCN模型 f s f_{s} fs )。
-
不可察觉性的损失:
触发器内边连接的节点余弦相似度要尽可能大
在所有节点上施加不磕察觉损失的约束,确保生成的触发器满足各类节点不可察觉约束
E B i \mathcal{E}_{B}^{i} EBi 是触发器 g i g_{i} gi 包含的边,以及连接触发器 g i g_{i} gi 与节点 v i v_{i} vi 的边。
min θ g L c = ∑ v i ∈ V ∑ ( v j , v k ) ∈ E B i max ( 0 , T − sim ( v j , v k ) ) , (3) \min _{\theta_{g}} \mathcal{L}_{c}=\sum_{v_{i} \in \mathcal{V}} \sum_{\left(v_{j}, v_{k}\right) \in \mathcal{E}_{B}^{i}} \max \left(0, T-\operatorname{sim}\left(v_{j}, v_{k}\right)\right),\tag{3} θgminLc=vi∈V∑(vj,vk)∈EBi∑max(0,T−sim(vj,vk)),(3)
-
代理模型训练:
min θ s L s ( θ s , θ g ) = ∑ v i ∈ V L l ( f s ( G C i ) , y i ) + ∑ v i ∈ V P l ( f s ( a ( G C i , g i ) ) , y t ) , (4) \min _{\theta_{s}} \mathcal{L}_{s}\left(\theta_{s}, \theta_{g}\right)=\sum_{v_{i} \in \mathcal{V}_{L}} l\left(f_{s}\left(\mathcal{G}_{C}^{i}\right), y_{i}\right)+\sum_{v_{i} \in \mathcal{V}_{P}} l\left(f_{s}\left(a\left(\mathcal{G}_{C}^{i}, g_{i}\right)\right), y_{t}\right), \tag{4} θsminLs(θs,θg)=vi∈VL∑l(fs(GCi),yi)+vi∈VP∑l(fs(a(GCi,gi)),yt),(4)
-
触发器优化:
将被附加触发器的节点(节点集中的各种类别节点)成功预测为目标类别
L g ( θ s , θ g ) = ∑ v i ∈ V l ( f s ( a ( G C i , g i ) ) , y t ) , (5) \mathcal{L}_{g}\left(\theta_{s}, \theta_{g}\right)=\sum_{v_{i} \in \mathcal{V}} l\left(f_{s}\left(a\left(\mathcal{G}_{C}^{i}, g_{i}\right)\right), y_{t}\right), \tag{5} Lg(θs,θg)=vi∈V∑l(fs(a(GCi,gi)),yt),(5)
-
综合可得双向优化问题:
min θ g L g ( θ s ∗ ( θ g ) , θ g ) + β L c ( θ g ) s.t. θ s ∗ = arg min θ s L s ( θ s , θ g ) , (6) \begin{array}{l} \min _{\theta_{g}} \mathcal{L}_{g}\left(\theta_{s}^{*}\left(\theta_{g}\right), \theta_{g}\right)+\beta \mathcal{L}_{c}\left(\theta_{g}\right) \\ \text { s.t. } \quad \theta_{s}^{*}=\arg \min _{\theta_{s}} \mathcal{L}_{s}\left(\theta_{s}, \theta_{g}\right), \tag{6} \end{array} minθgLg(θs∗(θg),θg)+βLc(θg) s.t. θs∗=argminθsLs(θs,θg),(6)
交替优化方案
-
第一层优化问题(第二行):更新下层代理模型
θ s t + 1 = θ s t − α s ∇ θ s L s ( θ s , θ g ) \theta_{s}^{t+1}=\theta_{s}^{t}-\alpha_{s} \nabla_{\theta_{s}} \mathcal{L}_{s}\left(\theta_{s}, \theta_{g}\right) θst+1=θst−αs∇θsLs(θs,θg)
-
第二层优化问题(第一行):更新上层代理模型
θ g k + 1 = θ g k − α g ∇ θ g ( L g ( θ ˉ s , θ g k ) + β L c ( θ g k ) ) \theta_{g}^{k+1}=\theta_{g}^{k}-\alpha_{g} \nabla_{\theta_{g}}\left(\mathcal{L}_{g}\left(\bar{\theta}_{s}, \theta_{g}^{k}\right)+\beta \mathcal{L}_{c}\left(\theta_{g}^{k}\right)\right) θgk+1=θgk−αg∇θg(Lg(θˉs,θgk)+βLc(θgk))
减小触发器的不可察觉性损失,并增加触发器注入后的预测准确率(攻击成功率)
-
-
实验探究的问题
-
能否有效的实施后门攻击并同时保持后门的不可察觉性
-
在四个数据集上,使用设置了防御的分类器,衡量UGBA的攻击表现和不可察觉性。
- 不使用防御策略时,UGBA性能优于其他基线方法,尤其在大型数据集上。这表明中毒节点选择算法充分利用了攻击预算。
-
所有基线方法在使用触发器检测的防御策略(Prune、Prune+LD)后的性能都非常差,但UGBA能够维持超过90%的平均成功率和较高的干净准确率。这表明了UGBA能够为后门攻击生成高效且不易被察觉的触发器。
-
由于是从3个不同GNN架构中取得的平均成功率结果,而较高的ASR分数,这表明UGBA是具有迁移性的。
-
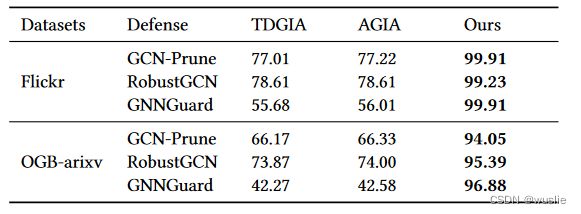
在大型图上,UGBA也能绕过鲁棒性GCN防御和触发器检测防御,取得不错的攻击性能
-
相较于节点注入攻击,UGBA只需要额外少量的注入触发器和目标标签的开销,但它的性能比节点注入攻击优30%。这表明UGBA在攻击大型图上具有优势。
-
-
中毒节点的数量对后门攻击的影响
-
攻击成功率随中毒样本数量的增加而增加
-
当Prune+LD防御方法应用于后门攻击时,仍有良好的性能,这是由于生成的触发器节点和被附加的节点相似,使其具有不可察觉的特性。
-
-
自适应约束模块和中毒节点选择模块对攻击性能的影响
- 消融实验,分别去掉不可察觉约束模块、中毒节点选择模块、以及两者皆去掉
实验设置
-
数据集:Cora、Pubmed、Flickr、OGB-arxiv
-
对比方法(超参都根据验证集的性能进行调整)
-
图后门攻击方法:GTA、SBA-Samp、SBA-Gen、GBAST
-
大型图上的图注入攻击方法(逃逸攻击):TDGIA、AGIA
-
-
与防御方法的对抗
-
Prune、Prune+LD:帮助估计后门攻击的不可察觉性
-
鲁棒性GNN:RobustGCN、GNNGuard,验证UGBA可以有效攻击一般的鲁棒GNN。
-
-
数据集设置
-
从原始数据集中mask掉20%的节点
-
一半用于攻击性能评估的目标节点
-
另一半作为干净的测试节点,用于评估后门模型在正常样本上的预测精度。
-
-
剩下80%的节点构成训练图 G G G ,其中有标签节点集和验证集均包含10%的节点
-
-
评估准则
-
平均成功率(ASR):目标节点集合上后门攻击的平均成功率
-
干净准确率:干净测试节点上的分类准确率
-
-
攻击的可转移性证明
-
攻击GCN、GraphSage、GAT等不同架构的GNN模型
-
每个模型上执行5次攻击,一共运行15次,取得平均成功率
-
-
目标类别设置:class 0
-
中毒节点数量设置:Cora=10、Pubmed=40、Flickr=80、OGB-arxiv=160
-
触发器大小:3
-
代理模型:2层GCN
-
自适应触发器生成:2层MLP