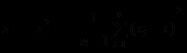数学之路(3)-数据分析(3)
本博客所有内容是原创,未经书面许可,严禁任何形式的转载。
http://blog.csdn.net/u010255642
2、位置描述指标
(1)平均值
> mean(jiuye[["平均劳动报酬"]])
[1] 42365.36
我们同时统计一下劳动报酬和教育经费的平均值
> cbind(jiuye[["平均劳动报酬"]],jiuye[["平均教育经费"]])
> apply(jiuyeinfo,2,mean)
[1] 42365.365 391.035
(2)加权平均值
读取产品成本数据,然后求产品平均单位成本
> read.table("h:/my_docs/cp.csv",,header=TRUE,sep=",")->cp
> cp
序号 产量.台. 单机成本.元.台.
1 1 4300 346.23
2 2 4004 343.34
3 3 4300 327.46
4 4 5016 313.27
5 5 5511 310.75
6 6 5648 307.61
7 7 5876 314.56
8 8 6651 305.72
9 9 6024 310.82
10 10 6194 306.83
11 11 7558 305.11
12 12 7381 300.71
13 13 6950 306.84
14 14 6471 303.44
15 15 6354 298.03
16 16 8000 296.21
> weighted.mean(cp$单机成本.元.台. ,cp$产量.台.)
[1] 309.9866
>
(3)数据排序
> sort(jiuye$平均教育经费)
[1] 0 0 0 2 2 2 6 7 7 8 10 13
[13] 27 30 31 31 31 32 35 37 38 42 42 44
[25] 46 50 51 55 55 62 63 65 66 66 67 71
[37] 72 72 75 75 76 80 89 92 93 93 95 95
[49] 100 100 100 100 100 105 109 110 111 115 118 119
[61] 125 136 138 143 144 145 146 147 147 149 149 157
[73] 159 161 161 162 162 166 168 168 168 172 177 177
[85] 182 184 186 188 190 196 196 196 200 201 206 210
[97] 210 212 212 221 224 225 230 230 241 241 247 247
[109] 258 260 267 267 276 276 277 282 295 295 298 299
[121] 303 304 305 306 308 314 315 317 330 332 337 340
[133] 341 342 348 367 369 371 374 374 389 389 396 402
[145] 405 409 416 422 422 423 431 436 443 454 455 461
[157] 466 470 486 502 522 524 535 551 551 554 555 557
[169] 563 571 582 645 679 682 692 722 738 753 768 782
[181] 818 830 832 840 840 858 890 890 890 986 995 1096
[193] 1131 1198 1255 1469 1553 2087 2564 12645
排序后,可以初步发现,这些行业的教育经费最大的有12645,而最小的除0之外只有2,不同行业之间的教育经费差异很大。
改变排序顺序:
> sort(jiuye$平均教育经费,decreasing=TRUE)
[1] 12645 2564 2087 1553 1469 1255 1198 1131 1096 995 986 890
[13] 890 890 858 840 840 832 830 818 782 768 753 738
[25] 722 692 682 679 645 582 571 563 557 555 554 551
[37] 551 535 524 522 502 486 470 466 461 455 454 443
[49] 436 431 423 422 422 416 409 405 402 396 389 389
[61] 374 374 371 369 367 348 342 341 340 337 332 330
[73] 317 315 314 308 306 305 304 303 299 298 295 295
[85] 282 277 276 276 267 267 260 258 247 247 241 241
[97] 230 230 225 224 221 212 212 210 210 206 201 200
[109] 196 196 196 190 188 186 184 182 177 177 172 168
[121] 168 168 166 162 162 161 161 159 157 149 149 147
[133] 147 146 145 144 143 138 136 125 119 118 115 111
[145] 110 109 105 100 100 100 100 100 95 95 93 93
[157] 92 89 80 76 75 75 72 72 71 67 66 66
[169] 65 63 62 55 55 51 50 46 44 42 42 38
[181] 37 35 32 31 31 31 30 27 13 10 8 7
[193] 7 6 2 2 2 0 0 0
>
(4)中位数
中位数比平均值更有稳健性,因为它不受偏态分布的影响。
> median(jiuye$平均教育经费)
[1] 222.5
与平均值有一定差距,说明平均教育经费不是对称分布的。
(5)百分位数
上四分位数和下四分位数比较重要
> quantile(jiuye$平均教育经费)
0% 25% 50% 75% 100%
0.0 100.0 222.5 425.0 12645.0
> quantile(jiuye$平均教育经费,probs=seq(0,1,0.1))
0% 10% 20% 30% 40% 50% 60% 70% 80%
0.0 37.9 75.8 123.2 168.0 222.5 300.6 378.5 506.0
90% 100%
785.6 12645.0
(6)数据分散程度度量
方差
> var(jiuye$平均教育经费)
[1] 883263.6
标准差
> sd(jiuye$平均教育经费)
[1] 939.821
变异系数
变异系数,又称“离散系数”,是概率分布离散程度的一个归一化量度,其定义为标准差与平均值之比,变异系数的计算公式为:
变异系数越小,变异(偏离)程度越小,风险也就越小;反之,变异系数越大,变异(偏离)程度越大,风险也就越大。
> sd(jiuye$平均教育经费)/mean(jiuye$平均教育经费)
[1] 2.403419
>
再看看平均劳动报酬的变异系数
> sd(jiuye$平均劳动报酬)/mean(jiuye$平均劳动报酬)
[1] 0.4916487
>
平均教育经费比平均劳动报酬分布相对更分散