【Pytorch笔记】7.torch.nn (Convolution Layers)
我们常用torch.nn来封装网络,torch.nn为我们封装好了很多神经网络中不同的层,如卷积层、池化层、归一化层等。我们会把这些层像是串成一个牛肉串一样串起来,形成网络。
先从最简单的,都有哪些层开始学起。
Convolution Layers - 卷积层
torch.nn.Conv1d()
1维卷积层。
torch.nn.Conv1d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros',
device=None,
dtype=None)
in_channels:输入tensor的通道数;
out_channels:输出tensor的通道数;
kernel_size:卷积核的大小;
stride:步长;
padding:输入tensor的边界填充尺寸;
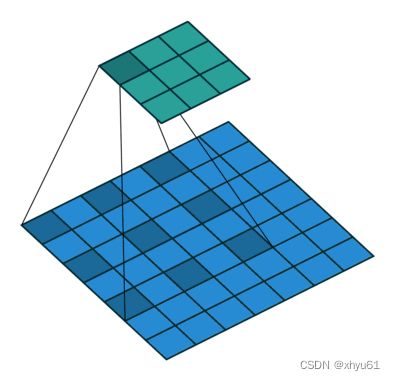
dilation:卷积核之间的间距(下面这个图为dilation=2),默认为1;
groups:从输入通道到输出通道的阻塞连接数。in_channel和out_channel需要能被groups整除。更具体地:
groups=1时所有输入均与所有输出进行卷积,groups=2时该操作相当于并排设置两个卷积层,每卷积层看到一半的输入通道,产生一半的输出通道,然后将两个卷积层连接起来。groups=in_channel时输入的每个通道都和相应的卷积核进行卷积;
bias:是否添加可学习的偏差值,True为添加,False为不添加。
padding_mode:填充模式,有以下取值:zeros(这个是默认值)、reflect、replicate、circular。
import torch
import torch.nn as nn
m = nn.Conv1d(in_channels=16,
out_channels=33,
kernel_size=3,
stride=2)
# input: 批大小为20,每个数据通道为16,size=50
input = torch.randn(20, 16, 50)
output = m(input)
print(output.size())
输出
# output: 批大小为20,每个数据通道为33,size=24
torch.Size([20, 33, 24])
torch.nn.Conv2d()
2维卷积层。
torch.nn.Conv2d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros',
device=None,
dtype=None)
参数与Conv1d()基本一样,不再赘述。
import torch
import torch.nn as nn
m = nn.Conv2d(in_channels=2,
out_channels=3,
kernel_size=3,
stride=2)
input = torch.randn(20, 2, 5, 6)
output = m(input)
print(output.size())
输出
torch.Size([20, 3, 2, 2])
torch.nn.Conv3d()
3维卷积层。
torch.nn.Conv3d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros',
device=None,
dtype=None)
参数与Conv1d()基本一样,不再赘述。
import torch
import torch.nn as nn
m = nn.Conv3d(in_channels=2,
out_channels=3,
kernel_size=3,
stride=2)
input = torch.randn(20, 2, 4, 5, 6)
output = m(input)
print(output.size())
输出
torch.Size([20, 3, 1, 2, 2])
torch.nn.ConvTranspose1d()
1维转置卷积层。
torch.nn.ConvTranspose1d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
output_padding=0,
groups=1,
bias=True,
dilation=1,
padding_mode='zeros',
device=None,
dtype=None)
参数与Conv1d()基本一样,不再赘述。
唯一不同的是output_padding,与padding不同的是,output_padding是输出tensor的每一个边,外面填充的层数。
(padding是输入tensor的每个边填充的层数)
import torch
import torch.nn as nn
m = nn.ConvTranspose1d(in_channels=2,
out_channels=3,
kernel_size=3,
stride=1)
input = torch.randn(20, 2, 2)
output = m(input)
print(output.size())
输出
torch.Size([20, 3, 4])
torch.nn.ConvTranspose2d()
2维转置卷积层。
torch.nn.ConvTranspose2d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
output_padding=0,
groups=1,
bias=True,
dilation=1,
padding_mode='zeros',
device=None,
dtype=None)
参数与Conv1d()基本一样,不再赘述。
import torch
import torch.nn as nn
m = nn.ConvTranspose2d(in_channels=2,
out_channels=3,
kernel_size=3,
stride=1)
input = torch.randn(20, 2, 2, 2)
output = m(input)
print(output.size())
输出
torch.Size([20, 3, 4, 4])
torch.nn.ConvTranspose3d()
3维转置卷积层。
torch.nn.ConvTranspose3d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
output_padding=0,
groups=1,
bias=True,
dilation=1,
padding_mode='zeros',
device=None,
dtype=None)
参数与Conv1d()基本一样,不再赘述。
import torch
import torch.nn as nn
m = nn.ConvTranspose3d(in_channels=2,
out_channels=3,
kernel_size=3,
stride=1)
input = torch.randn(20, 2, 2, 2, 2)
output = m(input)
print(output.size())
输出
torch.Size([20, 3, 4, 4, 4])
torch.nn.LazyConv1d()
1维延迟初始化卷积层,当in_channel不确定时可使用这个层。
关于延迟初始化,大家可以参考这篇文章,我认为讲的很好:
俱往矣… - 延迟初始化——【torch学习笔记】
torch.nn.LazyConv1d(out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros',
device=None,
dtype=None)
LazyConv1d没有in_channel参数。
这不代表这个层没有输入的通道,而是在调用时自动适配,并进行初始化。
引用文章中的一段代码,改成LazyConv1d,讲述使用方法。
import torch
import torch.nn as nn
net = nn.Sequential(
nn.LazyConv1d(256, 2),
nn.ReLU(),
nn.Linear(9, 10)
)
print(net)
[net[i].state_dict() for i in range(len(net))]
low = torch.finfo(torch.float32).min / 10
high = torch.finfo(torch.float32).max / 10
X = torch.zeros([2, 20, 10], dtype=torch.float32).uniform_(low, high)
net(X)
print(net)
输出
Sequential(
(0): LazyConv1d(0, 256, kernel_size=(2,), stride=(1,))
(1): ReLU()
(2): Linear(in_features=9, out_features=10, bias=True)
)
Sequential(
(0): Conv1d(20, 256, kernel_size=(2,), stride=(1,))
(1): ReLU()
(2): Linear(in_features=9, out_features=10, bias=True)
)
可以看出,未进行初始化时,in_features=0。只有传入参数使用网络后才会根据输入进行初始化。
torch.nn.LazyConv2d()
2维延迟初始化卷积层。
torch.nn.LazyConv2d(out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros',
device=None,
dtype=None)
torch.nn.LazyConv3d()
3维延迟初始化卷积层。
torch.nn.LazyConv3d(out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros',
device=None,
dtype=None)
torch.nn.LazyConvTranspose1d()
1维延迟初始化转置卷积层。
torch.nn.LazyConvTranspose1d(out_channels,
kernel_size,
stride=1,
padding=0,
output_padding=0,
groups=1,
bias=True,
dilation=1,
padding_mode='zeros',
device=None,
dtype=None)
torch.nn.LazyConvTranspose2d()
2维延迟初始化转置卷积层。
torch.nn.LazyConvTranspose2d(out_channels,
kernel_size,
stride=1,
padding=0,
output_padding=0,
groups=1,
bias=True,
dilation=1,
padding_mode='zeros',
device=None,
dtype=None)
torch.nn.LazyConvTranspose3d()
3维延迟初始化转置卷积层。
torch.nn.LazyConvTranspose3d(out_channels,
kernel_size,
stride=1,
padding=0,
output_padding=0,
groups=1,
bias=True,
dilation=1,
padding_mode='zeros',
device=None,
dtype=None)
torch.nn.Unfold()
从一个批次的输入张量中提取出滑动的局部区域块。
torch.nn.Unfold(kernel_size,
dilation=1,
padding=0,
stride=1)
kernel_size:滑动块的大小;
dilation:卷积核之间的间距(torch.nn.Conv1d中有图示);
padding:输入tensor的边界填充尺寸;
stride:滑块滑动的步长。
这里的输入必须是4维的tensor,否则会报这样的错误:
NotImplementedError: Input Error: Only 4D input Tensors are supported (got 2D)
示例
import torch
from torch import nn
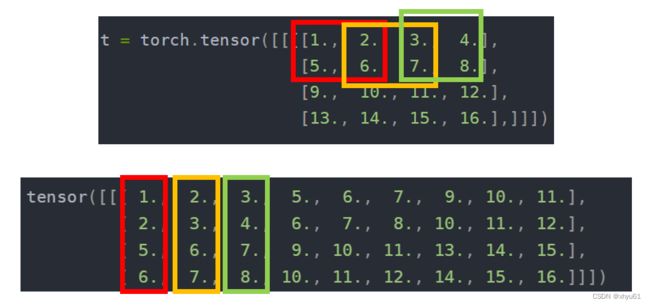
t = torch.tensor([[[[1., 2., 3., 4.],
[5., 6., 7., 8.],
[9., 10., 11., 12.],
[13., 14., 15., 16.],]]])
unfold = nn.Unfold(kernel_size=(2, 2), dilation=1, padding=0, stride=1)
output = unfold(t)
print(output)
输出
tensor([[[ 1., 2., 3., 5., 6., 7., 9., 10., 11.],
[ 2., 3., 4., 6., 7., 8., 10., 11., 12.],
[ 5., 6., 7., 9., 10., 11., 13., 14., 15.],
[ 6., 7., 8., 10., 11., 12., 14., 15., 16.]]])
torch.nn.Fold()
Unfold()的逆操作。当Unfold()时出现滑块有重复覆盖时会导致结果和原来不一样。因为Fold()的过程中对于同一个位置的元素进行加法处理。
torch.nn.Fold(output_size,
kernel_size,
dilation=1,
padding=0,
stride=1)
下面是Unfold()和Fold()结合的代码,Unfold()部分和上面代码相同。
import torch
from torch import nn
t = torch.tensor([[[[1., 2., 3., 4.],
[5., 6., 7., 8.],
[9., 10., 11., 12.],
[13., 14., 15., 16.]]]])
unfold = nn.Unfold(kernel_size=(2, 2), dilation=1, padding=0, stride=1)
output = unfold(t)
print(output)
fold = nn.Fold(output_size=(4, 4), kernel_size=(2, 2))
out = fold(output)
print(out)
输出
tensor([[[ 1., 2., 3., 5., 6., 7., 9., 10., 11.],
[ 2., 3., 4., 6., 7., 8., 10., 11., 12.],
[ 5., 6., 7., 9., 10., 11., 13., 14., 15.],
[ 6., 7., 8., 10., 11., 12., 14., 15., 16.]]])
tensor([[[[ 1., 4., 6., 4.],
[10., 24., 28., 16.],
[18., 40., 44., 24.],
[13., 28., 30., 16.]]]])