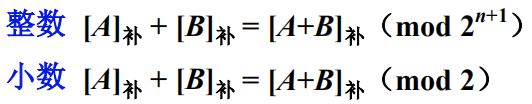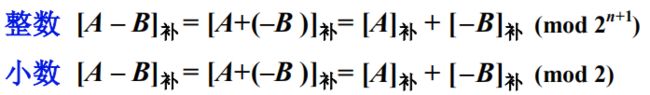计算机组成原理13-定点数的移位、加法与减法运算
目录
一、移位运算
1、移位的意义
2、算术移位规则
3.算术移位和逻辑移位的区别
二、加法与减法运算
1.补码加减运算的基本公式
2.溢出判断
(1)一位符号位判断溢出
(2)符号位和数值部分的最高位判溢出
(3)采用双符号位补码进行判断
补码的设计目的:
- 使符号位能与有效值部分一起参加运算,从而简化运算规则
- 使减法运算转换为加法运算,进一步简化计算机中运算器的线路设计
所有这些转换都是在计算机的最底层进行的,而在我们使用的汇编、C等其他高级语言中使用的都是原码。
定点数运算包括移位、加、减、乘、除几种。
一、移位运算
1、移位的意义
移位运算在日常生活中常见。例如:
- 15米可写作1500厘米,单就数字而言,1500相当于小数点左移了两位,并在小数点前面添了两个0;
- 同样15也相当于1500相对于小数点右移了两位,并删去了小数点后面的两个0。
- 可见,当某个十进制数相对于小数点左移n位时,相当于该数乘以10^n;右移n位时,相当于该数除以10^n。
计算机中小数点的位置是事先约定的,因此,二进制表示的机器数在相对于小数点作n位左移或右移时,其实质就便该数乘以或除以2^n(n=1,2...n)。
移位运算又叫移位操作,对计算机来说,有很大的实用价值,例如,当计算机没有乘(除)运算线路时,可以采用移位和加法相结合,实现乘(除)运算。
- 在计算机中,移位与加减配合,能够实现乘除运算
计算机中机器数的字长往往是固定的,当机器数左移n位或右移n位时,必然会使其n位低位或n位高位出现空位。那么,对空出的空位应该添补0还是1呢?
这与机器数采用有符号数还是无符号数有关,对有符号的移位叫算术移位。
2、算术移位规则
对于正数,由于 [x]原=[x]补=[x]反=真值 ,故移位后出现的空位均以0添之。
对于负数,由于原码、补码和反码的表示形式不同,故当机器数移位时,对其空位的添补规则也不同。
下表列出了三种不同码制的机器数(整数或小数均可),分别对应正数或负数,移位后的添补规则。
必须注意的是:不论是正数还是负数,移位后其符号位均不变,这是算术移位的重要特点。
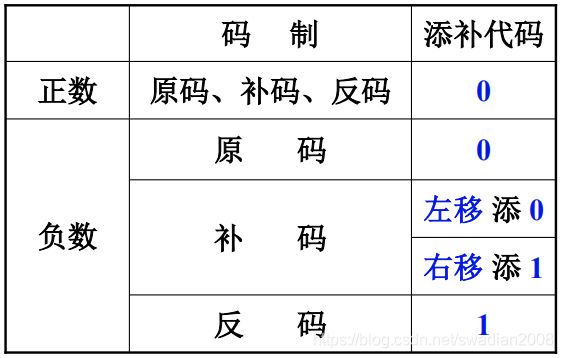
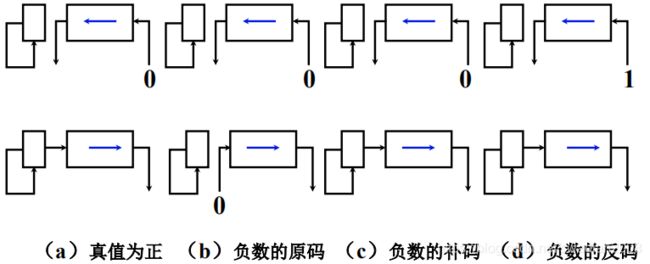
不同码制机器数移位后的空位添补规则
由上表可得出如下结论:
- 机器数为正数时,不论左移或右移,添补代码均为0。
- 由于负数的原码其数值部分与真值相同,故在移位时只要使符号位不变,其空位均添0。
- 由于负数的反码其各位除符号位外与负数的原码正好相反,故移位后所添的代码应与原码相反,即全部添1。
- 分析任意负数的补码可发现,当对其由低位向高位找到第一个“1”时,在此“1”左边的各位均与对应的反码相同,而在此“1”右边的各位(包括此“1”在内)均与对应的原码相同,即添0;
如1.1111100000的不同码制的值的比较:
- [x]原=1.1111100000
- [x]反=1.0000011111
- [x]补=1.0000100000 ——>"1" 右边的各位0与对应的原码相同,代表真值的0 ;"1"左边的各位0与对应的反码相同,代表真值的1
例:
- 设机器数字长为8位(含一位符号位),若A=±26,写出三种机器数左、右移一位和两位后的表示形式及对应的真值,并分析结果的正确性。
解:
(1)当A = +26 = +11010(二进制码),机器数字长为8位,则 [A]原=[A]补=[A]反=0,0011010
移位结果表示如下:
可见,对于正数,三种机器数移位后符号位不变,左移时最高数位丢1,结果出错;右移时最低数位丢1,影响精度。
(2)当 A = -26 = -11010(二进制码),三种机器数移位结果示于下表
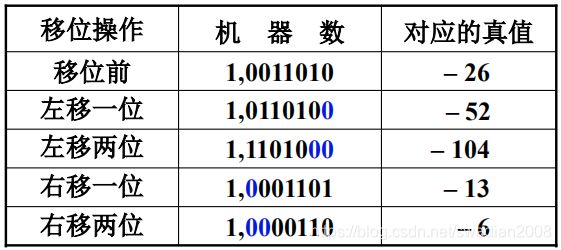
原码
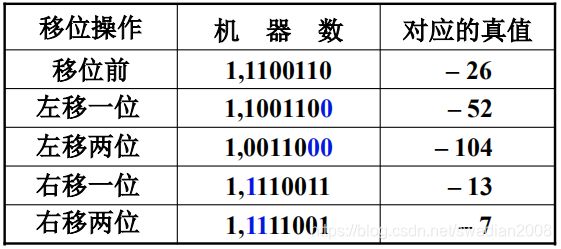
补码
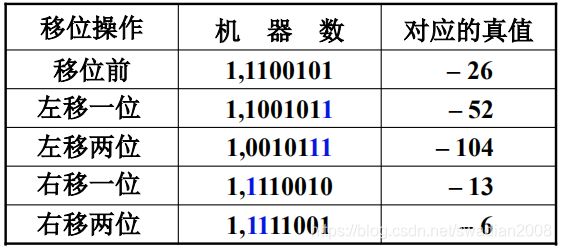
反码
可见,对于负数,三种机器数移位后符号位均不变。
- 负数的原码左移时,高位丢1,结果出错;低位丢1,影响精度。
- 负数的补码左移时,高位丢0,结果出错;低位丢1,影响精度。
- 负数的反码左移时,高位丢0,结果出错;低位丢0,影响精度。
下图示意了机器中实现算术左移和右移操作的硬件框图
3.算术移位和逻辑移位的区别
有符号数的移位称为算术移位,无符号数的移位称为逻辑移位。
逻辑移位的规则是:
- 逻辑左移时,高位移出,低位添0;
- 逻辑右移时,低位移出,高位添0。
例如
- 寄存器内容为01010011,逻辑左移为1010010,算术左移为00100110(最高数位“1”移丢)。
- 又如寄存器内容为10110010,逻辑右移为01011001。若将其视为补码,算术右移为11011001。
显然,两种移位的结果是不同的。
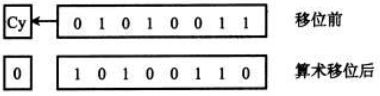
上例中为了避免算术左移时最高数位丢1,可采用带进位(Cy)的移位,其示意图如下图所示。算术左移时,符号位移至Cy,最高数位就可避免移出。
二、加法与减法运算
减法运算是计算机中最基本的运算,因减法运算可看作被减数加上一个减数的负值,即A-B=A+(-B),故在此将机器中的减法运算和加法运算合在一起讨论。
现代计算机中都采用补码作加减法运算。
1.补码加减运算的基本公式
补码加法的基本公式为:
即补码表示两个数在进行加法运算时,可以把符号位与数位同等处理,只要结果不超出机器能表示的数值范围,运算后的结果按2^(n+1)取模(对于整数);或按2取模(对于小数),就能得到本次加法的运算结果。
对于减法,因 A-B=A+(-B),则 [A-B]补=[A+(-B)]补
由补码加法基本公式可得:
因此,若机器数采用补码, 当求A-B时, 只需先求[-B]补(称[-B]补为“求补”后的减数),就可按补码加法规则进行运算。而[-B]补由[B]补连同符号位在内,每位取反,末位加1而得。
例:A=0.1010,B=-0.0101,用补码的加法求A+B
[A]补=0.1011,[B]补=1.1011
[A]补+[B]补 = 0.1011+1.1011=0.0110(按模2的意义,最左边的1丢掉),所以 A+B=0.0110
例:x=0.1001,y=-0.0011,用补码的减法求x-y
解:[x]补=0.1001,[y]补=1.1101,[-y]补=0.0011
[x]补-[y]补=[x]补+[-y]补=0.1001+0.0011=0.1100,所以 x-y=0.1100
例:设机器数字长为8位,其中一位为符号位,令A=-93,B=+45,求[A-B]补。
解:由A=-93=-1011101,得[A]补=1,0100011,由B=+45=+0101101,得[B]补=0,0101101,[-B]补=1,1010011
[A-B]补=[A]补+[-B]补=1,0100011+1,1010011=10,1110110
按模2^(n+1)的意义,最左边的“1”自然丢掉,故[A-B]补=0,1110110,还原成真值得A-B=118,结果出错,这是因为A-B=-138超出了机器字长所能表示的范围。在计算机中,这种超出机器字长的现象,叫溢出。为此,在补码定点加减运算过程中,必须对结果是否溢出作出明确的判断。
2.溢出判断
补码定点加减运算判断溢出有三种方法。
(1)一位符号位判断溢出
对于加法,只有在正数加正数和负数加负数两种情况下才可能出现溢出,符号不同的两个数相加是不会出现溢出的。
对于减法,只有在正数减负数或负数减正数两种情况下才可能出现溢出,符号相同的两个数相减是不会出现溢出的。
因此在判断溢出时可以根据参加运算的两个数据和结果的符号位进行。
两个符号位相同的补码相加,如果和的符号位与加数的符号相反,则表明运算结果溢出;
两个符号位相反的补码相减,如果差的符号位与被减数的符号位相反,则表明运算结果溢出。
这种方法需要判断操作是加法还是减法,以及运算结果与操作数的符号关系。
(2)符号位和数值部分的最高位判溢出
利用数据编码的最高位(符号位)和次高位(数值部分的最高位)的进位状况来判断运算结果是否发生了溢出。
两个补码数实现加减运算时,若最高数值位向符号位的进位值与符号位产生的进位输出值不相同,则表明加减运算产生了溢出。
因为当x和y均为n+1位正整数时,其和有两种情况:
- 当x+y<2^n时,不会发生溢出;
- 当x+y≥2^n时符号位没有进位,表明发生溢出。
当x和y都是n+1位负数时,其和也有两种情况:
- 当x+y≥-2^n时,不会发生溢出;
- 当x+y<-2^n时,符号位相加后变成0并且有进位,而数值部分的最高位相加时无进位,结果变为正数,表明发生了溢出。
减法的情况与此类似,这种判断方法的逻辑表达式如下:
例:设x=+1011, y=+1001,求[x+y]补。
解:[x]补=01011, [y]补=01001
[x+y]补=01011+01001=10100
两个正数相加,最高两位的进位为01,表示发生了溢出,其结果为负数,显然是错误的。
例:设x=-1101,y=-1011,求[x+y]补。
解:[x]补=10011, [y]补=10101
[x+y]补=10011+10101=01000
两个负数相加,最高两位的进位为10,表示发生了溢出,其结果为正数,显然是错误的。
(3)采用双符号位补码进行判断
正常时两个符号位的值相同,在运算结果中当两个符号位不同时则表明发生了溢出。
运算结果的符号位为01表明两个正数相加,结果大于机器所能表示的最大正数,称为上溢;
运算结果的符号位为10表明两个负数相加,结果小于机器所能表示的最小负数,称为下溢。
也就是说,两个正数相加,数值位不应向符号位同时产生进位,使得结果数的符号位和操作数的一样,为00:
- 00+00+00(进位) = 00 (mod 4)
两个负数相加,数值位应向符号位产生进位,使得两个负数的双符号位的运算为11:
- 11+11+01(进位)=11(mod 4)
当运算结果的两个符号位不相同时,表明出现了溢出。
例:设x=+1100,y=+1000,求6位双符号位补码之和[x+y]补。
解:[x]补=001100, [y]补=001000
[x+y]补=001100+001000=010100
[x+y]补=010100,其中两个符号位出现01,表示已溢出。
例:设x=-1100,y=-1000,求6位双符号位补码之和[x+y]补。
解:[x]补=110100, [y]补=111000
[x+y]补=110100+111000=101100
[x+y]补=101100,其中两个符号位出现10,表示已溢出。
从上述例子中还看出,不论溢出与否,最高位始终指示正确的符号。
采用双符号位补码后,任何小于1的正数,两个符号位都是0;任何大于-1的负数,两个符号位都是1。
如果两个数相加后,其结果的符号位出现01或10时,表示发生溢出。因为两个绝对值小于1的数相加,其结果不会大于或等于2,所以最高位总是表示正确的符号。这也可以表示为:
当最高数据位有进位而符号位无进位时产生上溢出;当最高数据位无进位而符号位有进位时,表示下溢出。
在双符号位补码中,正常的数据中两个符号位总是相同的,所以在存储数据时不必重复存储,只是在将数据送往运算部件进行运算时才把符号位进行复制形成双符号位补码。