数据结构实验报告-二叉树的存储结构的实现与应用
实验目的
熟悉二叉树结点的结构和对二叉树的基本操作。
掌握对二叉树每一种操作的具体实现。
学会利用递归方法编写对二叉树这种递归数据结构进行处理的算法。
在二叉树基本操作的基础上掌握二叉树的应用。
实验要求
1. 独立完成;
2. 程序调试正确,有执行结果。
3. 程序是自己开发的,在运行结果界面上输出显示姓名。
- 基础题:
按照教材中关于二叉树的抽象数据类型定义,采用二叉链表存储结构,编程实现二叉树的各种基本操作,并通过主函数调用,简单测试各基本函数的正确性。
比如:二叉树的基本操作可包括:
(1) void InitBT( BTreeNode *&BT ) //初始化二叉树BT
(2) void CreateBT( BTreeNode *&BT, char *a )
//根据字符串a所给出二叉树的描述,建立二叉链表存储结构
(3) int EmptyBT( BTreeNode *BT)
//检查二叉树BT是否为空,空返回1,否则返回0
(4) int DepthBT( BTreeNode *BT) //求二叉树BT的深度并返回该值
(5) int NodeCount(BTreeNode *BT) //求二叉树BT的总结点个数
(6) void PreOrder( BTreeNode *BT) //先序遍历递归算法
(7) void InOrder( BTreeNode *BT) //中序遍历递归算法
(8) void PostOrder( BTreeNode *BT) //后序遍历递归算法
(9) int FindBT( BTreeNode *BT, ElemType x)
//查找二叉树BT中值为x的结点,若查找成功返回1,否则返回0
(10)void DestroyBT( BTreeNode *&BT ) //销毁二叉树BT
2.应用题
(1)采用二叉链表存储结构,完成二叉树的层次遍历,先序遍历的非递归算法和中序遍历的非递归算法。
(2)采用二叉链表存储结构,交换二叉树中每个结点的左孩子和右孩子。
(3)哈夫曼编码器
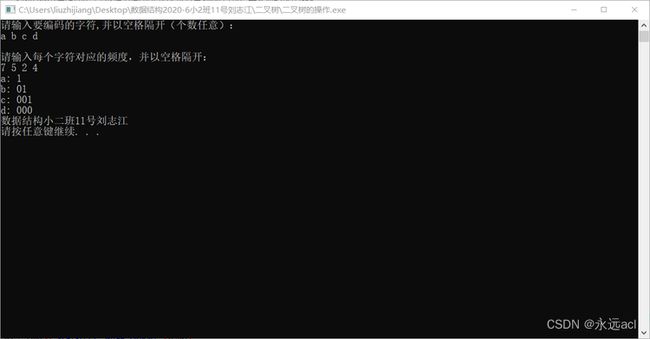
给定n(n=5,n=8,n=15,n=27)个字符在某个系统中出现的概率,以该n个概率做叶子结点的权值,根据Huffman算法,构造一棵哈夫曼树,给n个字符编码
3
【实验内容】1.需求分析
按照上机实验报告模板格式,写出二叉链表存储结构的二叉树的上机实验的需求分析。(不要用上传附件形式)
正确答案:
我的答案:
特性
二叉树中每个结点最多有两棵子树;二叉树每个结点的度小于等于2
子树有左右之分,不能颠倒——有序树
二叉树是递归结构,在二叉树的定义中又用到了二叉树的概念
在树型结构中,二叉树的结构最简单,规律性最强;
可以证明,所有树都能转为唯一对应的二叉树。二叉树也能转换成树或森林。
普通树(多叉树)若不转化为二叉树,则运算很难实现。
4
【实验内容】2.概要设计
按照上机实验报告模板,写出二叉树的抽象数据类型定义ADT,其他模块(如果有)和函数的功能说明,本程序包含的函数列表,函数之间的调用关系。(不要用上传附件形式,调用关系可上传图片)
正确答案:
我的答案:
ADT BinaryTree {
数据对象:D 是具有相同特性的数据元素的集合。
数据关系:
若D为空集,则称为空树。
否则:
(1) 在D中存在唯一的称为根的数据元素 root;
(2) 当n > 1时,其余结点可分为2个互不相交的有限集T1、T2,其中每一个子集本身又是一棵符合本定义的二叉树,T1称为根 root 的左子树,T2称为根 root 的右子树。
基本操作:
初始化操作
InitBiTree (&T)操作结果:构造空二叉树 T。
CreateBiTree (&T, definition)初始条件:definition 给出二叉树 T 的定义。
操作结果:按 definition 构造二叉树 T。
结构销毁操作
DestroyBiTree (&T);
初始条件:二叉树 T 存在。
操作结果:销毁二叉树 T 。
Root ( T )
初始条件:二叉树 T 存在。
操作结果:返回二叉树T的根结点。
Value ( T, e )
初始条件:二叉树 T 存在,e 是 T 中某个结点。
操作结果:返回e的值。
Parent ( T, e )
初始条件:二叉树 T 存在,e 是 T 中某个结点。
操作结果:若e是T的非根结点,则返回它的双亲,
否则返回“空”。
LeftChild ( T, e )
初始条件:二叉树 T 存在,e 是 T 中某个结点。
操作结果:返回 e 的左孩子。若 e 无左孩子,
则返回"空"。
RightChild ( T, e )
初始条件:二叉树 T 存在,e 是 T 中某个结点。
操作结果:返回 e 的右孩子。若 e 无右孩子,
则返回"空" 。
LeftSibling ( T, e )
初始条件:二叉树 T 存在,e 是 T 中某个结点。
操作结果:返回 e 的左兄弟。若 e 是其双亲的
左孩子或无左兄弟,则返回“空”。
RightSibling ( T, e )
初始条件:二叉树 T 存在, e 是 T 中某个结点。
操作结果:返回 e 的右兄弟。若 e 是其双亲的
右孩子或无右兄弟,则返回"空"。
BiTreeEmpty (T);
初始条件:二叉树 T 存在。
操作结果:若T为空二叉树,则返回 TRUE,否则
返回 FALSE。
BiTreeDepth (T)
初始条件:二叉树 T 存在。
操作结果:返回 T 的深度。
PreOrderTraverse (T)——根左右(先序遍历)
初始条件:二叉树 T 存。
操作结果:先序遍历 T,对每个结点访问一次。
InOrderTraverse (T)——左根右(中序遍历)
初始条件:二叉树 T 存在。
操作结果:中序遍历 T,对每个结点访问一次。
PostOrderTraverse (T)——左右根(后序遍历)
初始条件:二叉树 T 存在。
操作结果:后序遍历 T,对每个结点访问一次。
LevelOrderTraverse (T)——(层次遍历)
初始条件:二叉树 T 存在。
操作结果:层序遍历 T,对每个结点访问一次。
Assign (&T, &e, value )
初始条件:二叉树 T 存在,e 是 T 中某个结点。
操作结果:结点 e 赋值为 value。
ClearBiTree ( &T )
初始条件:二叉树 T 存在。
操作结果:将二叉树 T 清为空树。
InsertChild ( &T, p, LR, c )
初始条件:二叉树 T 存在,p 指向 T 中某个结点,LR 为 0 或 1,非空二叉树 c 与 T 不相交且右子树为空。
操作结果:根据 LR 为 0 或 1,插入 c 为 T 中 p 所指结点的左或右子树。p 所指结点原有左或右子树成为 c 的右子树。
DeleteChild (&T, p, LR);
初始条件:二叉树 T 存在,p 指向 T 中某个结点,LR 为 0 或 1。
操作结果:根据 LR 为 0 或 1,删除 T 中 p 所指结点的左或右子树。
6
【实验内容】3.详细设计
按照上机实验报告模板,写出二叉链表存储结构的上机实验的详细设计部分:
1)实现概要设计中定义的所有的数据类型;
2)对每个操作对应的各个函数给出详细的伪码。
3)对主程序和其他模块(如果有)也写出详细的伪码;
4)分析各个函数的时间复杂度和空间复杂度。(递归的除外)
二叉树的基本操作
#include
cout<<"树已初始化"<<endl;
cout<<"创建树,'#'结束"<<endl;
creast(mytree);
if(empty(mytree))
{
cout<<"树为空树,重新创建"<<endl;
creast(mytree);
}
else{
cout<<"二叉树非空"<<endl;
}
cout<<"先序遍历:";
xxbl(mytree);
cout<<endl;
cout<<"中序遍历:";
zxbl(mytree);
cout<<endl;
cout<<"后序遍历:";
hxbl(mytree);
cout<<endl;
cout<<"该树的深度:"<<depth(mytree)<<endl;
cout<<"该树所有结点数为:"<<node(mytree)<<endl;
char a;
cout<<"输入一个字符进行查找"<<endl;
cin>>a;
if(find1(mytree,a))
{
cout<<"存在该字符"<<endl;
bitree p;
p=find2(mytree,a);
cout<<p->data;
}
else cout<<"不存在该字符"<<endl;
destory(mytree);
cout<<"程序结束摧毁树"<<endl;
cout<<"数据结构小二班11号刘志江"<<endl;
return 0;
}
二叉树的遍历
#include
cout<<"树已初始化"<<endl;
cout<<"创建树,'#'结束"<<endl;
creast(mytree);
if(empty(mytree))
{
cout<<"树为空树,重新创建"<<endl;
creast(mytree);
}
else{
cout<<"二叉树非空"<<endl;
}
cout<<"先序遍历:";
xxbl(mytree);
cout<<endl;
cout<<"中序遍历:";
zxbl(mytree);
cout<<endl;
cout<<"后序遍历:";
hxbl(mytree);
cout<<endl;
cout<<"该树的深度:"<<depth(mytree)<<endl;
cout<<"该树所有结点数为:"<<node(mytree)<<endl;
char a;
cout<<"输入一个字符进行查找"<<endl;
cin>>a;
if(find1(mytree,a))
{
cout<<"存在该字符"<<endl;
bitree p;
p=find2(mytree,a);
cout<<p->data;
}
else cout<<"不存在该字符"<<endl;
destory(mytree);
cout<<"程序结束摧毁树"<<endl;
cout<<"数据结构小二班11号刘志江"<<endl;
return 0;
}
二叉树的子树交换
#include>a;
if(find1(mytree,a))
{
cout<<"存在该字符"<data;
}
else cout<<"不存在该字符"<
cout<<"数据结构小二班11号刘志江"<<endl;
return 0;
}
哈夫曼
#include 即心得体会,包括对算法的讨论、分析,改进设想和其它经验教训等 。
正确答案:
我的答案:
在对于树的各种基本操作时要清晰的知道停止树的条件
在对树的左右子树的交换时可以另加一棵树,也可以在原树上进行交换。
在树的大多数操作中都采用了递归的算法