数据结构与算法-图
图
- 2.图的存储结构
-
-
- 2.4.2邻接表的存储
-
- ✅2.4.2.1逆邻接表
- ✅2.4.2.2邻接表存储结构的定义
- ✅2.4.2.3邻接表存储结构的类定义
- ✅2.4.2.4创建n个顶点m条边的无向网
- ✅2.4.2.5创建n个顶点m条边的有向网
- ✅2.4.2.6定位操作-查找定点信息在顶点数组中的下标
- ✅2.4.2.7计算顶点的度数-以无向网为例
- ✅2.4.2.8插入操作-以无向网为例
-
- 3.图的遍历
-
- 3.1深度优先搜索
-
- 3.1.1深度优先搜索算法(邻接表存储)
- 3.2广度优先搜索
-
- 3.2.1广度优先搜索算法(邻接表存储)
- 3.3以连通无向图为例进行广度优先搜索和深度优先搜索
2.图的存储结构
2.4.2邻接表的存储
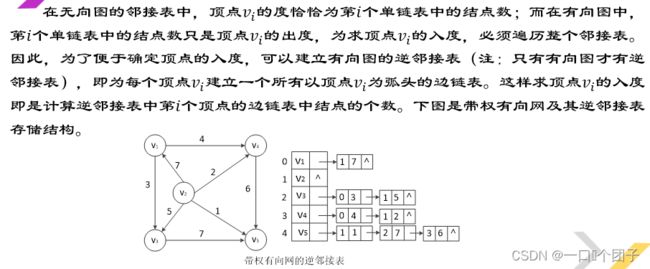
根据邻接表的定义可知,对于n个顶点和e条边的无向图,其邻接表有n个表头结点和2e个边结点。对于n个结点和e条边的有向图,其邻接表有n个表头结点和e个边结点。
✅2.4.2.1逆邻接表
✅2.4.2.2邻接表存储结构的定义
#define MaxVex 20//自定义最大顶点数
typedef enum
{
DG,UDG,DN,UDN
}GraphKind;//有向图,无向图,有向网,无向网
typedef int VElemType;
typedef struct ArcNode//边结点定义
{
int adjvex;//终点(或弧尾)在数组表中的下标
int info;///该边(弧)相关信息(权值)
ArcNode* nextarc;//存储下一条边(或弧)结点的地址
}ArcNode;
typedef struct//表头结点的定义
{
VElemType data;
ArcNode* firstarc;//存储第一条依附该顶点的边(或弧)结点地址
}VNode;
typedef struct
{
VNode vertices[MaxVex];
int vexnum;
int arcnum;
GraphKind kind;
}AdjLGraph;
✅2.4.2.3邻接表存储结构的类定义
class ALGraph
{
private:
AdjLGraph ag;
public:
void CreateGraph(int n, int m);//创建n个顶点,m条边的图,以无向网为例
int LocateVex(VElemType u);//图中存在顶点u,则返回该顶点在数组中的下标,否则返回-1
int Degree(VElemType u);//计算顶点u的度数
void InsertArcGraph(VElemType u, VElemType v, int info);//插入一条边
void BFS(VElemType v);//以v为初始点的连通分量的广度优先搜索
void DFS(VElemType v);//以v为初始点的连通分量的深度优先搜索
void BFSTraverse();//图的广度优先搜索
void DFSTreverse();//图的深度优先搜索
int Connected();//计算连通分量的个数
Edge* Kruskal();//Kruskal算法求最小生成树
Edge* Prim(VElemTyp u);//prim算法求最小生成树
int TopSort();//拓扑排序
int CriticalPath();//求关键路径
AdjLGraph GetAg()
{
return ag;//返回私有成员
}
};
✅2.4.2.4创建n个顶点m条边的无向网
void ALGraph::CreateGraph(int n, int m)//以无向网为例
{
ag.vexnum = n;
ag.arcnum = m;
ag.kind = UDN;
int i, j, w, h, t;
VElemType u, v;
ArcNode* p;
for (i = 0; i < n; i++)
{
cout << "请输入" << n << "个顶点:";
cin >> ag.vertices[i].data;
ag.vertices[i].firstarc = NULL;
}
for (j = 0; j < m; j++)//建立边集
{
cin >> u >> v >> w;//输入一条弧✅2.4.2.5创建n个顶点m条边的有向网
void ALGraph::CreateGraph(int n, int m)
{
ag.vexnum = n;
ag.arcnum = m;
ag.kind = UDN;
int i, j, w, h, t;
VElemType u, v;
ArcNode* p;
for (i = 0; i < n; i++)
{
cout << "请输入" << n << "个顶点:";
cin >> ag.vertices[i].data;
ag.vertices[i].firstarc = NULL;
}
for (j = 0; j < m; j++)//建立边集
{
cin >> u >> v >> w;//输入一条弧✅2.4.2.6定位操作-查找定点信息在顶点数组中的下标
int ALGraph::LocateVex(VElemType u)
{
for (int i = 0; i < ag.vexnum; i++)
{
if (u == ag.vertices[i].data)
return i;
}
return -1;
}
✅2.4.2.7计算顶点的度数-以无向网为例
int ALGraph::Degree(VElemType u)
{
int h = LocateVex(u);//结点u的下标
int count = 0;
ArcNode* p = ag.vertices[h].firstarc;//p指向第h条链表的第一个结点
while (p)
{
count++;
p = p->nextarc;
}
return count;
}
✅2.4.2.8插入操作-以无向网为例
void ALGraph::InsertArcGraph(VElemType u, VElemType v, int info)//无向网为例
{
int h = LocateVex(u);
int t = LocateVex(v);
ArcNode* p;
if (h == -1)
{
ag.vertices[ag.vexnum].data = u;
ag.vertices[ag.vexnum].firstarc = NULL;
h = ag.vexnum;
ag.vexnum++;
}
if (t == -1)
{
ag.vertices[ag.vexnum].data = v;
ag.vertices[ag.vexnum].firstarc = NULL;
t = ag.vexnum;
ag.vexnum++;
}
p = new ArcNode;
p->adjvex = t;
p->info = info;
p->nextarc = ag.vertices[h].firstarc;
ag.vertices[h].firstarc = p;
p = new ArcNode;
p->adjvex = h;
p->info = info;
p->nextarc = ag.vertices[t].firstarc;
ag.vertices[t].firstarc = p;
ag.arcnum++;
}
3.图的遍历
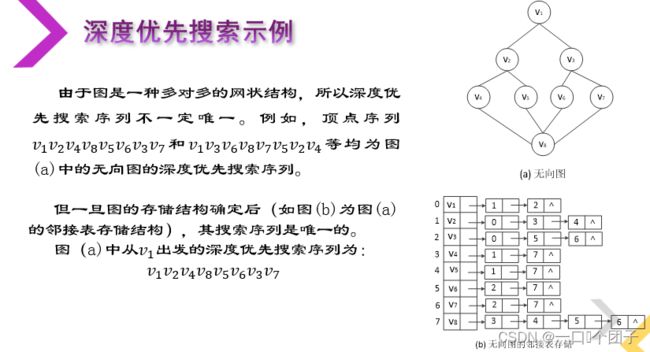
3.1深度优先搜索
✅深度优先搜索类似于树的先序遍历,是树的先序遍历的推广。深度优先搜索是一个不断探查和回溯的过程,具体过程如下:
- 从图中某顶点v出发,访问顶点v
- 从v的未被访问过的邻接点中选择一个顶点出发,继续对图进行深度优先遍历。若从图中某个顶点出发的所有邻接点都已被访问过,则退回前一个结点继续上述过程,若退回初始点,则以v为初始点的搜索结束。
- 若为非连通图,图中尚有未被访问过的顶点,则另选图中一个未曾访问过的顶点作为初始点,重复上述过程,直到图中所有顶点均被访问为止。
❗说明:
- 若无向图是连通图,则一次遍历就能访问图中所有的顶点。
- 若无向图是非连通图,则只能访问到初始点所在连通分量中的所有顶点,还需要从其他分量中再选择初始点,分别进行遍历才能访问到图中所有顶点。
- 对于有向图来说,若从初始点到图中每个顶点都有路径,则一次遍历能够访问图中所有顶点,否则,同样需要在选择初始点继续进行遍历,直到图中所有顶点均被访问为止。
3.1.1深度优先搜索算法(邻接表存储)
int visited[MaxVex];//访问标志数组,初始化所有元素值为0
void ALGraph::DFS(VElemType v)//以v为初始点的连通分量的深度优先搜索算法如下
{
ArcNode* p;
int h = LocateVex(v);
cout << v;//访问该顶点
visited[h] = 1;//置访问标记为1
for (p = ag.vertices[h].firstarc; p; p = p->nextarc)
{
if (visited[p->adjvex] == 0)
DFS(ag.vertices[p->adjvex].data);
}
}
void ALGraph::DFSTreverse()//对图作深度优先搜索
{
int i;
for (i = 0; i < ag.vexnum; i++)
{
visited[i] = 0;//访问标志初始化
}
for (i = 0; i < ag.vexnum; i++)
{
if (!visited[i])//对尚未访问的顶点调用DFS
DFS(ag.vertices[i].data);
}
}
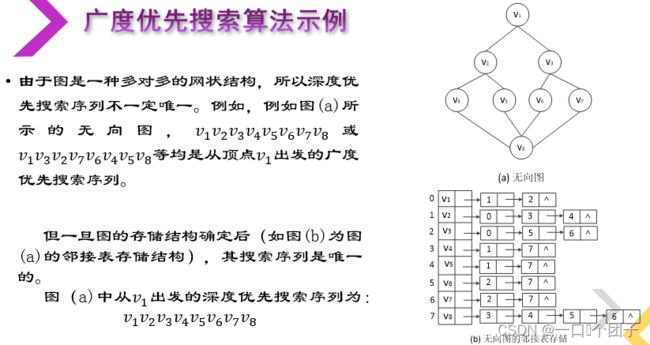
3.2广度优先搜索
广度优先搜索类似于树的层次遍历方法,其搜索过程如下:
- 访问初识顶点v
- 访问与v相邻的所有未被访问的邻接点w1,w2,w3…wk
- 依次从这些邻接点出发,访问它们的所有未被访问的邻接点。
- 依次类推,直到连通图中所有访问过的顶点的邻接点都被访问。
- 若为非连通图,图中尚有未被访问过的顶点,则另选图中的一个未曾访问过的顶点作为初始点,重复上述过程,直到图中所有顶点均被访问过为止。
3.2.1广度优先搜索算法(邻接表存储)
void ALGraph::BFS(VElemType v)//以v为初始点的连通分量的广度优先搜索
{
int h = LocateVex(v);
ArcNode* p;
LinkQueue lq;
lq.DeQueue(h);
visited[h] = 1;
while (!lq.EmptyQueue())
{
lq.DeQueue(h);
cout << ag.vertices[h].data;
for (p = ag.vertices[h].firstarc; p; p = p->nextarc)
{
if (!visited[p->adjvex])
{
lq.EnQueue(p->adjvex);
visited[p->adjvex] = 1;
}
}
}
}
void ALGraph::BFSTraverse()
{
int i;
for (i = 0; i < ag.vexnum; i++)
{
visited[i] = 0;
}
for (i = 0; i < ag.vexnum; i++)
{
if (!visited[i])
BFS(ag.vertices[i].data);
}
}
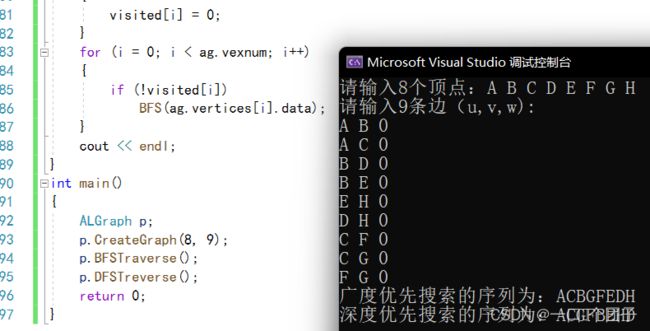
3.3以连通无向图为例进行广度优先搜索和深度优先搜索
#define _CRT_SECURE_NO_WARNINGS 1
#include