一文看懂Word2Vec

后来我才知道，它并不是我的花，我只是恰好途径了它的盛放。

什么是Word2Vec

NLP的目标是要理解语言，而语言的基本单位则是单词word。对于只与0/1打交道的机器来说，他们无法理解单词的实际含义，因此我们需要将单词变为数字，这样才能进行后续的分析计算，而这个过程我们称之为word embedding。一个数字显然是无法记录一个单词的完整语义信息的，因此实际我们都是将一个单词映射为一个向量，我们称之为词向量。而我们要介绍的Word2Vec就是word embedding的一个重要算法。但是在真正进入word2vec前，我们先要了解一些前置知识。

前人在词向量化上做了很多工作，其中提出了一个很重要的假设——分布式假设：某个单词的含义由它周围的单词形成。基于这个假设，word embedding也涌现出了不少算法，主要分为基于计数的算法和基于推理的算法。基于计数的算法较为简单，如构建共现矩阵等等，这里不多做阐述。下面主要谈谈基于推理的算法。

基于推理的算法

基于推理的算法核心原理在于，给定目标单词的上下文，猜测目标位置会出现什么单词。举例：文本为I like drink beer. 我们要对drink做word2vec，则我们需要根据I like ? beer，猜测？处会出现什么单词。换言之，模型的输入是这个单词的上下文，输出是语料库中各个单词填在这的概率。预测各个词的概率和这个词的词向量有什么关系呢？后面我们可以看到，模型的权重就是这个词对应的词向量。

另外，这里需要介绍一下one-hot编码。假设语料库有N个单词，one-hot编码就是长度为N的向量，初始默认所有值为0。对于第i个单词，它的one-hot编码就是将第i个位置改为1。举例：语料库：['I', 'love', 'apple']，I对应的one-hot编码就是（1，0，0），love对应的one-hot编码是（0，1，0），apple对应的编码是（0，0，1）。

word2vec主要包含两个模型，CBOW和Skip-gram，我们下面来进行介绍。

CBOW模型

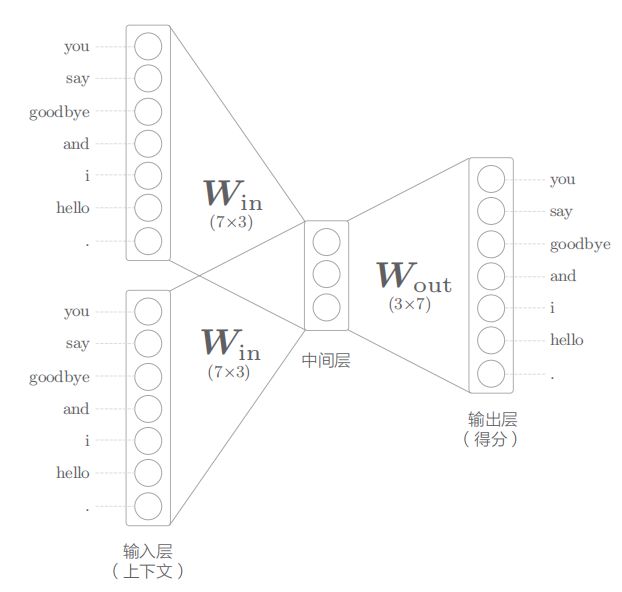
原版word2vec提出的模型叫CBOW（continous bag-of-word）。该模型网络如下：

模型整体结构比较简单，主要包含三层：输入层，中间层，输出层。上图展示的是上下文各取一个单词的情形，因此有两个输入层，也就是一个输入层对应一个单词（输入层左边的单词是语料库，便于查看one-hot编码）。输入层输入的是这个单词的one-hot编码，两个输入层经过W_in（7*3）得到各自对应的中间层编码向量（长度为3），再进行加权平均，即得到中间层向量。随后中间层经过W_out（3*7）得到该单词的得分，最后经过softmax，就可以得到该单词填充在目标位置的概率。

我们注意到W_in是所有输入层共享的，实际上W_in里就保存着每个单词的词向量表示。由于我们输入的单词是one-hot编码，在进行矩阵乘法时，实际上会把对应位置的W_in矩阵中的向量提取出来（对应位置为1），得到中间表示。而这个中间表示，则是将单词信息压缩后得到的向量。换言之，权重中的第i行对应第i个单词的词向量表示。

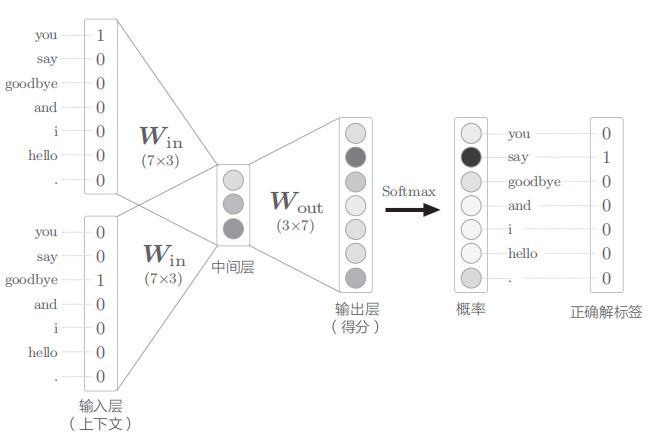
我们以图中的例子举例，假设一句话为you say goodbye and i say hello，我们想要得到第一个say的词向量。上下文为you和goodbye：

通过上图中的流程，我们可以组出多组上下文与其对应的标签，我们利用这些数据进行训练，损失采用经典的交叉熵损失。最后得到的权重即为单词的词向量表示。

Skip-gram模型

word2vec的另一个模型就是skip-gram模型。与CBOW相反，这个模型是通过单词本身来预测它的上下文。

模型也比较类似，只是这回输入层只有一个，输出层有两个：

具体原理和CBOW类似，这里不多做介绍。两个方法的对比如下：

• Skip-gram任务更难，实际表现效果更好

• CBOW学习速度更快，训练成本更低

Word2vec优化

输入层优化

我们注意到，在上述的CBOW模型中，当语料库非常大的时候，会产生很大的矩阵乘法开销。考虑我们输入层采用的one-hot编码，矩阵乘法的意义不过是将对应位置的W_in中的权重取出来，因此我们可以省去这个MatMul层，用一个新的层来将对应位置的权重直接从矩阵中取出来，我们叫它Embedding层。

Embedding层的具体实现这里不过多说明，我们可以显然看到这样省去了输入层MatMul的开销，是个简单而又非常有效的优化。

中间层及以后的优化

中间层及以后主要有两部分开销：一部分是中间层的大矩阵乘法（中间向量*W_out），另外一个是softmax部分。我们首先的优化思路是将多分类问题转为二分类，例如上述的多分类任务是在语料库中选择一个最合适的单词，我们可以将其转换为最合适的单词是不是xxx（xxx为正确标签的单词）。这样转换后，我们的输出层只有一个神经元，可以直接取出对应标签的列进行矩阵运算。具体来说，假设中间层为维度为（1，100），W_out维度为（100，1000000），那么原始的MatMul需要进行（1，100）*（100，1000000）的大矩阵运算，得到一个（1，1000000）的分数向量，再进行Softmax多分类。而我们优化后，则只需要进行（1，100）*（100，1）的运算，得到（1，1）的输出，也就是一个数，随后进行二分类。

二分类我们采用Sigmoid激活函数+交叉熵损失进行实现，由于这些是深度学习比较基础的内容，这里不多做赘述。优化后的网络结构图如下：

至此，我们还没完全将多分类转为二分类，因为我们只处理了正样本（只对正确的样本进行学习），所以我们还需要进行负采样。由于语料库很大，我们不可能对所有单词进行负采样学习，实际上我们只需要提取出频率最高的几个单词就可以了。