PyTorch神经网络-激励函数

在PyTorch 神经网络当中，使用激励函数处理非线性的问题，普通的神经网络出来的数据一般是线性的关系，但是遇到比较复杂的数据的话，需要激励函数处理一些比较难以处理的问题，非线性结果就是其中的情况之一。

---

FAQ:为什么要使用激励函数？

• 在简易乃至复杂的神经网络当中，对于神经元的数据结果为线性的时候，可能就会导致后面预测无法达到预期的效果，线性可能是一个不具体的一个范围，所以需要加入激励函数（一般是非线性的）去将数据进行处理

---

在少量的神经网络当中，一般使用 RELU激励函数，而在比较复杂的神经网络（包含循环神经网络RNN）当中，一般会使用 RELU或者 TANH函数进行处理

激励函数 Activation

下图为 Kaggle 编写的四种激励函数，分别是（relu，sigmoid，tanh和softplus）

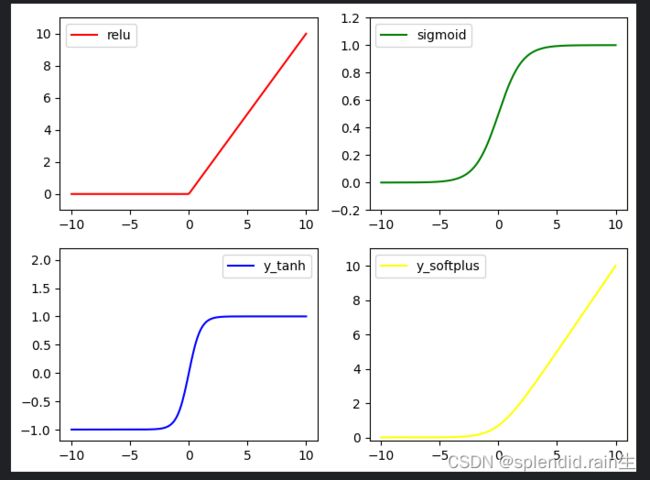
可以看到上面四个激励函数当x轴为输出的数据，可以理解成为神经网络的输出结果，然后将神经网络素输出结果加入激活函数，也就四上图四个激励函数对应的y轴数据，经过了激励函数处理之后，结果就有了限制，这个就是不同的激励函数带来的不同效果

程序源码：

import torch
import torch.nn.functional as F

from torch.autograd import Variable
import matplotlib.pyplot as plt

# fake
x = torch.linspace(-10,10,200)
x = Variable(x)
x_np = x.data.numpy()  # change the value to tensor


y_relu = F.relu(x).data.numpy()
y_sigmoid = F.sigmoid(x).data.numpy()
y_tanh = F.tanh(x).data.numpy()
y_softplus = F.softplus(x).data.numpy()


plt.figure(1,figsize=(8,6))
plt.subplot(221)
plt.plot(x_np,y_relu,c='red',label='relu')
plt.ylim((-1,11))
plt.legend(loc='best')


plt.subplot(222)
plt.plot(x_np,y_sigmoid,c='green',label='sigmoid')
plt.ylim((-0.2,1.2))
plt.legend(loc='best')


plt.subplot(223)
plt.plot(x_np,y_tanh,c='blue',label='y_tanh')
plt.ylim((-1.2,2.2))
plt.legend(loc='best')


plt.subplot(224)
plt.plot(x_np,y_softplus,c='yellow',label='y_softplus')
plt.ylim((-0.2,11))
plt.legend(loc='best')

神经网络浅试

当了解了神经网络相关的原理之后，可以尝试着结合激励函数进行一个简单的Demo编写
主要氛围以下几个步骤：
（1）创建数据集->(2)建立神经网络->（3）训练数据->预测（显示验证可选）

1. 创建数据集

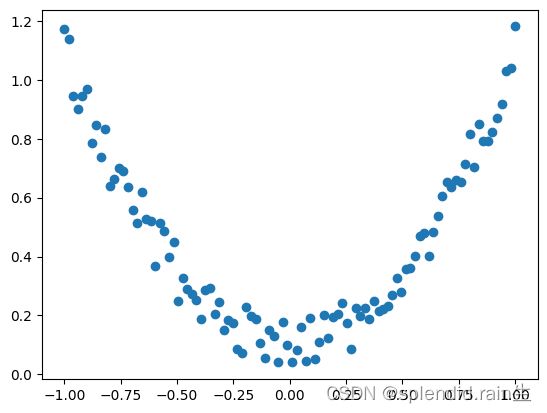
建立一些数据，去模拟真实的情况比如一个一元二次函数: y = a * x^2 + b, 我们给 y 数据加上一点噪声来更加真实的展示它。

import torch
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())                 # noisy y data (tensor), shape=(100, 1)

# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

2. 建立一个神经网络：

我们可以直接运用 torch 中的体系. 先定义所有的层属性(init()), 然后再一层层搭建(forward(x))层于层的关系链接. 建立关系的时候, 我们会用到激励函数。

import torch
import torch.nn.functional as F     # 激励函数都在这

class Net(torch.nn.Module):  # 继承 torch 的 Module
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()     # 继承 __init__ 功能
        # 定义每层用什么样的形式
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 隐藏层线性输出
        self.predict = torch.nn.Linear(n_hidden, n_output)   # 输出层线性输出

    def forward(self, x):   # 这同时也是 Module 中的 forward 功能
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.predict(x)             # 输出值
        return x

net = Net(n_feature=1, n_hidden=10, n_output=1)

print(net)  # net 的结构
"""
Net (
  (hidden): Linear (1 -> 10)
  (predict): Linear (10 -> 1)
)
"""

3.训练网络

训练的步骤如下：

# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)  # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss()      # 预测值和真实值的误差计算公式 (均方差)

for t in range(100):
    prediction = net(x)     # 喂给 net 训练数据 x, 输出预测值

    loss = loss_func(prediction, y)     # 计算两者的误差

    optimizer.zero_grad()   # 清空上一步的残余更新参数值
    loss.backward()         # 误差反向传播, 计算参数更新值
    optimizer.step()        # 将参数更新值施加到 net 的 parameters 上

4.可视化训练的过程

import matplotlib.pyplot as plt

plt.ion()   # 画图
plt.show()

for t in range(200):

    ...
    loss.backward()
    optimizer.step()

    # 接着上面来
    if t % 5 == 0:
        # plot and show learning process
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

结合上述步骤，总结出代码如下，在这里的程序更改的训练次数为 100次

import torch 
import torch.nn.functional as F

from torch.autograd import Variable
import matplotlib.pyplot as plt  # 数据可视化处理工具


# 输出数据
x = torch.unsqueeze(torch.linspace(-1,1,100),dim  =1)
y = x.pow(2) + 0.2*torch.rand(x.size())  # x 的二次方 + 一些随机噪点


plt.scatter(x.data.numpy(),y.data.numpy())
plt.show()


# 定义神经网络
class Net(torch.nn.Module):
    def __init__(self,n_features,n_hidden,n_output):
        # 搭建层所需要的信息
        super(Net,self).__init__()  # 初始化函数继承
        self.hidden = torch.nn.Linear(n_features,n_hidden)  # 隐藏层包含了，少的输出和输出
        self.predict = torch.nn.Linear(n_hidden,1)  # 输出值为 1，只是一个值
        
        
    
    def forward(self,x):
        # 前一层的信息,也就是x
        x = F.relu(self.hidden(x))  # 激励函数激活
        x = self.predict(x)  # 输出x
        return x


# Net(1,100,1)中的1表示输出数据为1个，100 为神经元个数，最后的1表示输出的数据，也是为1
net = Net(1,100,1)
print(net)


# 优化
optimizer = torch.optim.SGD(net.parameters(),lr = 0.5) # lr < 1
loss_function = torch.nn.MSELoss()

plt.ion()
plt.show()


for t in range(100):
    prediction = net(x)
    
    loss = loss_function(prediction,y)
    optimizer.zero_grad()  # 将传进来的参数的地图设置为零
    loss.backward()  # 反向传递过程
    optimizer.step()  # 优化梯度
    
    if t % 5 == 0:
        plt.cla()
        plt.scatter(x.data.numpy(),y.data.numpy())
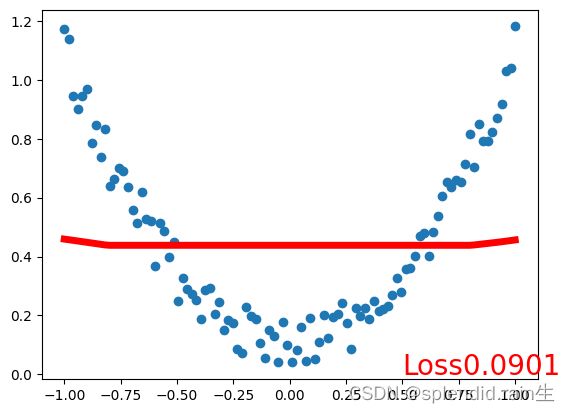
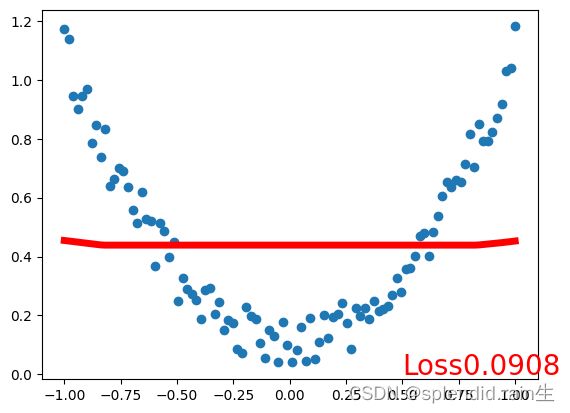
        plt.plot(x.data.numpy(),prediction.data.numpy(),'r-',lw=5)
        plt.text(0.5,0,'Loss%.4f'%loss.data.numpy(),fontdict={'size':20,'color':'red'})
        plt.pause(0.1)
plt.ioff()
plt.show()

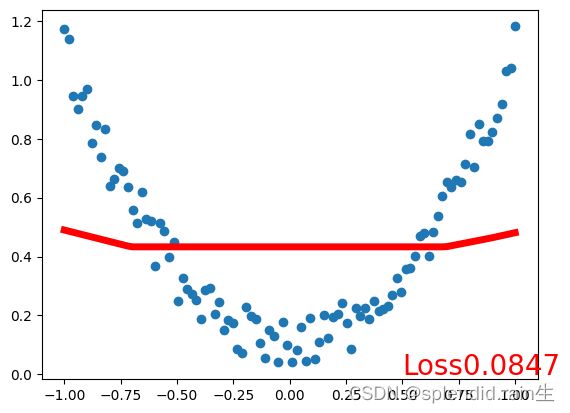
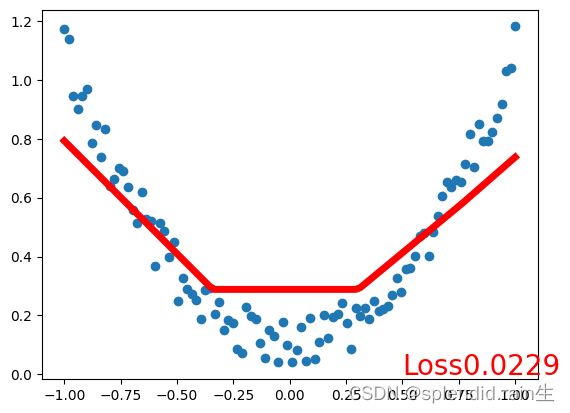
最后一张图为训练拟合的结果图，可以看到，红色的预测线将传入的随机点有了很接近的拟合，说明神经网络内的训练和优化有了很大的效果。

---

完结撒花

---

Redamancy