最长回文子序列问题-动态规划-范围尝试模型

最长回文子序列问题

题目：给定一个字符串str，返回这个字符串的最长回文子序列长度
比如 ： str = “12a343b2a1”
最长回文子序列是“1234321”，返回长度7。aba也是回文，只不过不是最长回文子序列

这里说明一下:子序列是可以不连续的，而子串是必须连续的，回文是正反过来练都一样

先考虑一个字符的情况

public static int f(char[] str, int L, int R) {
    if (L == R) {
       return 1;
    }
    if (L == R - 1) {
       // 如果一致相当于正反一样，就返回2
       return str[L] == str[R] ? 2 : 1;
    }
}

再考虑多种情况

​ 直接写暴力递归的可能性：

1. 既不以L开头，也不以R结尾
2. 以L开头，不以R结尾
3. 不以L开头，以R结尾
4. 既以L开头，也以R结尾
  	1. L，R位置字符不想等，可能性不存在
  	2. L，R位置字符要相等

int p1 = f(str, L + 1, R - 1);
int p2 = f(str, L, R - 1);
int p3 = f(str, L + 1, R);
// 这里加2是L...R中的一个回文子序列长度，所以加一个2
// 比如L...R是a123321a L和R位置都是a，那就直接算中间的位置，看看里面的最长回文子序列，然后再加上现有的a位置的2
int p4 = str[L] != str[R] ? 0 : (2 + f(str, L + 1, R - 1));
return Math.max(Math.max(p1, p2), Math.max(p3, p4));

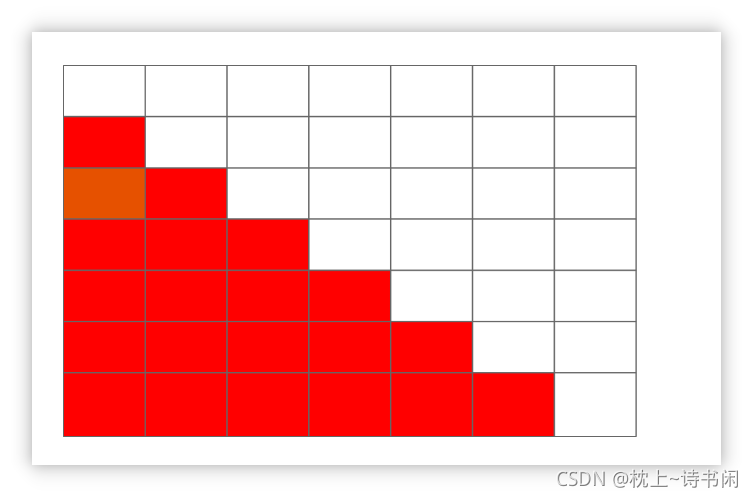
我们来想一下dp表的形式：

L…R代表一个范围，因为L比R大，所以在左下半区都没有用，左下半部分的情况都不可能出现。

接下来我们继续看递归

	if (L == R) {
       return 1;
    }
    if (L == R - 1) {
       // 如果一致相当于正反一样，就返回2
       return str[L] == str[R] ? 2 : 1;
    }

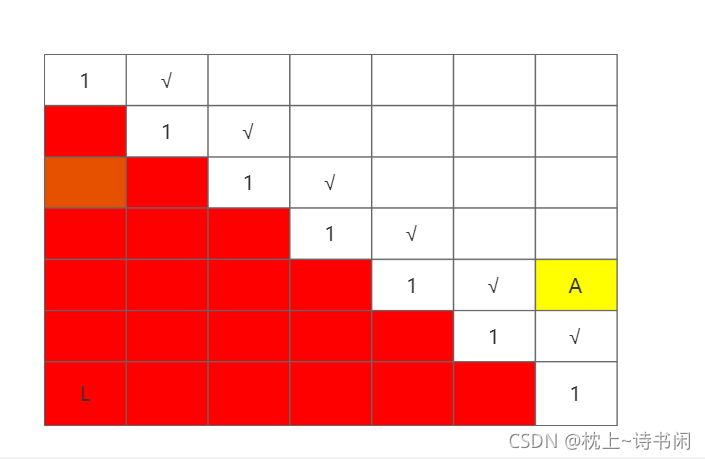
L==R的时候都是1

L==R-1相当于就是第二条对角线，str[L] == str[R]的时候相等就是2，不等就是1。

比如：abcdcba 下标0位置a和b不相等，然后dp表中[0，1] 位置就填1，接着看下表1和2，b和c也不想等，所以dp[1,2] 位置就填入1，依此类推，填完第二条对角线。

这里可以这么写，先将最右下角填1

dp[N - 1][N - 1] = 1;

for (int i = 0; i < N - 1; i++) {
   dp[i][i] = 1;
   dp[i][i + 1] = str[i] == str[i + 1] ? 2 : 1;
}

这样写的话就可以不用加多余的一些判断，然后可以两条对角线一起填。

那他的依赖位置是什么，我们依旧看递归：

int p1 = f(str, L + 1, R - 1);
int p2 = f(str, L, R - 1);
int p3 = f(str, L + 1, R);
int p4 = str[L] != str[R] ? 0 : (2 + f(str, L + 1, R - 1));

比如我现在要填A位置的值，那么看递归他是依赖于哪些位置

1. L + 1, R - 1 A位置左下角的位置
2. L, R - 1 A位置左边的位置
3. L + 1, R A位置左边的位置

第四种情况其实就是第一种情况。所以依赖三个位置:左边，下边，左下角

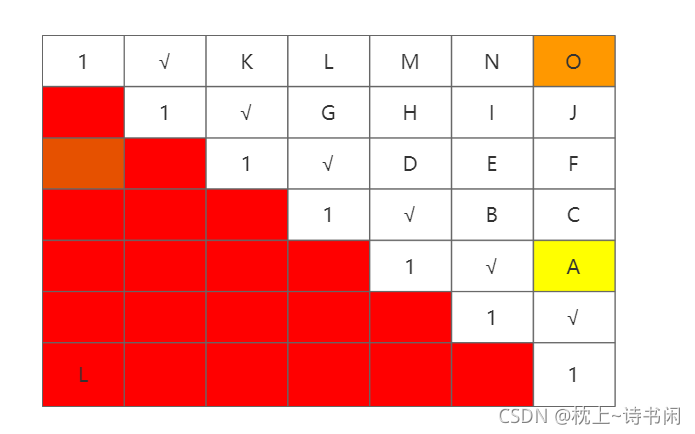
我们现在已经填好了，两条对角线的位置，那么我们其实可以从A位置往上一直推，直接推到 [N-1,R] 位置

相当于就是从下往上填，每一行从左往右填。从N-3开始

public static int dp(String s) {
   if (s == null || s.length() == 0) {
      return 0;
   }
   char[] str = s.toCharArray();
   int N = str.length;
   int[][] dp = new int[N][N];
   dp[N - 1][N - 1] = 1;
   for (int i = 0; i < N - 1; i++) {
      dp[i][i] = 1;
      dp[i][i + 1] = str[i] == str[i + 1] ? 2 : 1;
   }
   for (int L = N - 3; L >= 0; L--) {
      for (int R = L + 2; R < N; R++) {
         dp[L][R] = Math.max(dp[L][R - 1], dp[L + 1][R]);
         if (str[L] == str[R]) {
            dp[L][R] = Math.max(dp[L][R], 2 + dp[L + 1][R - 1]);
         }
      }
   }
   return dp[0][N - 1];
}

L = N-3 位置相当于就是画好了两条对角线。

L从L+2开始填写相当于就是从A位置出发。

那倒这里还有没有优化空间呢？

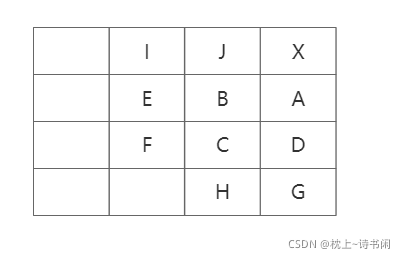
我们来看，A位置上面推出来是依赖于B、C、D位置的值，然后A是不可能比B、C、D位置小的，那么B位置也是依赖于C、E、F，D位置呢是依赖于C、H、G位置。那么我现在要求A位置的值，B和D里面都是有包含C了，如果C是最大值，那么肯定就是会在B或D里面了，所以我们只需要求左边位置和下面位置就行了，然后还有相等情况下的 [ i+1] [ j -1]+2的情况。

for (int i = N - 3; i >= 0; i--) {
   for (int j = i + 2; j < N; j++) {
      dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
      if (str[i] == str[j]) {
         dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - 1] + 2);
      }
   }
}

递归的语义是很大的，但不是所有递归都能改动态规划的，但是任何动态规划都可以由递归改过来，但不是所有的递归都属于动态规划。这里我们只是在有限的范围内去尽可能的找到最优解。

建立空间感的之后是可以继续优化的

范围模型：特别讨论开头和结尾共同结合的可能性，只讨论最长回文子序列的开头跟结尾。

一个问题有多个答案，一定要多写尝试