GRU、LSTM、双向循环神经网络
动手学深度学习笔记
- 一、门控循环单元(GRU)
-
- 1.重置门和更新门
- 2.候选隐状态
- 3.隐状态
- 4.PyTorch代码
- 二、长短期记忆网络(LSTM)
-
- 1.输入门、遗忘门和输出门
- 2.记忆元
- 3.隐状态
- 4.PyTorch代码
- 三、深度循环神经网络
- 四、双向循环神经网络
学习GRU和LSTM之前可以先看 RNN基础代码-PyTorch 这篇博客
一、门控循环单元(GRU)
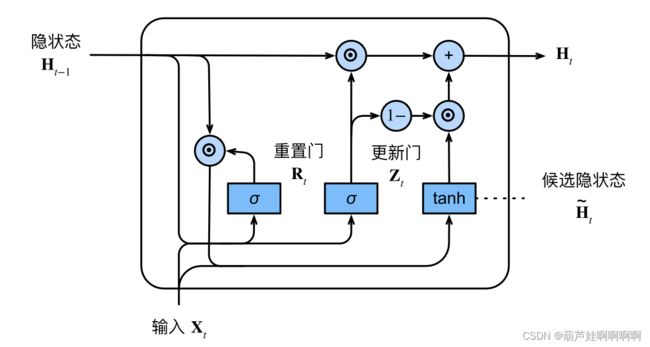
1.重置门和更新门
重置⻔允许我们控制“可能还想记住”的过去状态的数量;更新⻔将允许我们控制新状态中有多少个是旧状态的副本。
 $$ \pmb{R}_t=\sigma(\pmb{X}_t\pmb{W}_{xr}+\pmb{H}_{t-1}\pmb{W}_{hr}+\pmb{b}_r) \\ \pmb{Z}_t=\sigma(\pmb{X}_t\pmb{W}_{xz}+\pmb{H}_{t-1}\pmb{W}_{hz}+\pmb{b}_z) $$`两个⻔的输出是由使用sigmoid激活函数的两个全连接层给出。`
$$ \pmb{R}_t=\sigma(\pmb{X}_t\pmb{W}_{xr}+\pmb{H}_{t-1}\pmb{W}_{hr}+\pmb{b}_r) \\ \pmb{Z}_t=\sigma(\pmb{X}_t\pmb{W}_{xz}+\pmb{H}_{t-1}\pmb{W}_{hz}+\pmb{b}_z) $$`两个⻔的输出是由使用sigmoid激活函数的两个全连接层给出。`
2.候选隐状态
时间步t的候选隐状态 H ~ t ∈ R n × h \pmb{\tilde H}_t \in \mathbb R^{n×h} H~H~H~t∈Rn×h,计算如下:

H ~ t = t a n h ( X t W x h + ( R t ⊙ H t − 1 ) W h h + b h ) \pmb{\tilde H}_t=tanh(\pmb{X}_t\pmb{W}_{xh}+(\pmb{R}_{t}\odot \pmb{H}_{t-1})\pmb{W}_{hh}+\pmb{b}_h) H~H~H~t=tanh(XXXtWWWxh+(RRRt⊙HHHt−1)WWWhh+bbbh)
其中,符号⊙是Hadamard积(按元素乘积)运算符, R t \pmb{R}_{t} RRRt和 H t − 1 \pmb{H}_{t-1} HHHt−1 的元素相乘可以减少以往状态的影响。用非线性激活函数 t a n h tanh tanh来确保候选隐状态中的值保持在区间(−1, 1)中。
3.隐状态
H t = Z t ⊙ H t − 1 + ( 1 − Z t ) ⊙ H ~ t \pmb{H}_t=\pmb{Z}_t\odot\pmb{H}_{t-1}+(1-\pmb{Z}_{t})\odot\pmb{\tilde H}_t HHHt=ZZZt⊙HHHt−1+(1−ZZZt)⊙H~H~H~t
每当更新⻔ Z t \pmb{Z}_t ZZZt 接近1时,模型就倾向只保留旧状态。此时,来自 X t \pmb{X}_t XXXt 的信息基本上被忽略。相反,当 Z t \pmb{Z}_t ZZZt 接近0时,新的隐状态 H t \pmb{H}_t HHHt 就会接近候选隐状态 H ~ t \pmb{\tilde H}_t H~H~H~t 。
小结:
这些设计可以帮助处理RNN中的梯度消失问题,并更好地捕获时间步距离很⻓的序列的依赖关系。
例如,如果整个子序列的所有时间步的更新⻔都接近于1,则无论序列的⻓度如何,在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。
⻔控循环单元具有以下两个显著特征:
• 重置⻔有助于捕获序列中的短期依赖关系。
• 更新⻔有助于捕获序列中的⻓期依赖关系。
4.PyTorch代码
- 从零实现
import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
def get_params(vocab_size, num_hiddens, device):
"""初始化模型参数"""
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device)*0.01
def three():
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xz, W_hz, b_z = three() # 更新门参数
W_xr, W_hr, b_r = three() # 重置门参数
W_xh, W_hh, b_h = three() # 候选隐状态参数
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
def init_gru_state(batch_size, num_hiddens, device):
"""隐状态的初始化函数"""
return (torch.zeros((batch_size, num_hiddens), device=device), )
def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = H @ W_hq + b_q
outputs.append(Y)
return torch.cat(outputs, dim=0), (H,)
- 训练
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_params,
init_gru_state, gru)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

- 简洁实现
# 简洁实现
num_inputs = vocab_size
gru_layer = nn.GRU(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
二、长短期记忆网络(LSTM)
1.输入门、遗忘门和输出门

I t = σ ( X t W x i + H t − 1 W h i + b i ) F t = σ ( X t W x f + H t − 1 W h f + b f ) O t = σ ( X t W x o + H t − 1 W h o + b o ) \pmb{I}_t=\sigma(\pmb{X}_t\pmb{W}_{xi}+\pmb{H}_{t-1}\pmb{W}_{hi}+\pmb{b}_i) \\ \pmb{F}_t=\sigma(\pmb{X}_t\pmb{W}_{xf}+\pmb{H}_{t-1}\pmb{W}_{hf}+\pmb{b}_f)\\ \pmb{O}_t=\sigma(\pmb{X}_t\pmb{W}_{xo}+\pmb{H}_{t-1}\pmb{W}_{ho}+\pmb{b}_o) IIIt=σ(XXXtWWWxi+HHHt−1WWWhi+bbbi)FFFt=σ(XXXtWWWxf+HHHt−1WWWhf+bbbf)OOOt=σ(XXXtWWWxo+HHHt−1WWWho+bbbo)由三个具有sigmoid激活函数的全连接层处理,以计算输入⻔、遗忘⻔和输出⻔的 值,三个⻔的值都在(0, 1)的范围内。
2.记忆元
候选记忆元:
C ~ t = t a n h ( X t W x c + H t − 1 W h c + b c ) \pmb{\tilde C}_t=tanh(\pmb{X}_t\pmb{W}_{xc}+\pmb{H}_{t-1}\pmb{W}_{hc}+\pmb{b}_c) C~C~C~t=tanh(XXXtWWWxc+HHHt−1WWWhc+bbbc)
记忆元:
C t = F t ⊙ C t − 1 + I t ⊙ C ~ t \pmb{C}_t=\pmb{F}_t\odot\pmb{C}_{t-1}+\pmb{I}_{t}\odot\pmb{\tilde C}_t CCCt=FFFt⊙CCCt−1+IIIt⊙C~C~C~t
如果遗忘⻔始终为1且输入⻔始终为0,则过去的记忆元 C t − 1 \pmb{C}_{t-1} CCCt−1 将随时间被保存并传递到当前时间步。
引入这种设计是为了缓解梯度消失问题,并更好地捕获序列中的⻓距离依赖关系。
3.隐状态
H t = O t ⊙ t a n h ( C t ) \pmb{H}_t=\pmb{O}_t\odot tanh(\pmb{C}_t) HHHt=OOOt⊙tanh(CCCt)
H t \pmb{H}_t HHHt的值始终在区间(−1, 1)内,只要输出⻔接近1,我们就能够有效地将所有记忆信息传递给预测部分,而对于输出⻔接近0,我们只保留记忆元内的所有信息,而不需要更新隐状态。

小结
- ⻓短期记忆网络有三种类型的⻔:输入⻔、遗忘⻔和输出⻔。
- ⻓短期记忆网络的隐藏层输出包括“隐状态”和“记忆元”。只有隐状态会传递到输出层,而记忆元完全属于内部信息。
- ⻓短期记忆网络可以缓解梯度消失和梯度爆炸。
4.PyTorch代码
- 从零实现LSTM
import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
def get_lstm_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device)*0.01
def three():
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xi, W_hi, b_i = three() # 输入门参数
W_xf, W_hf, b_f = three() # 遗忘门参数
W_xo, W_ho, b_o = three() # 输出门参数
W_xc, W_hc, b_c = three() # 候选记忆元参数
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
b_c, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
W_hq, b_q] = params
(H, C) = state
outputs = []
for X in inputs:
I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)
F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)
O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)
C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)
C = F * C + I * C_tilda
H = O * torch.tanh(C)
Y = (H @ W_hq) + b_q
outputs.append(Y)
return torch.cat(outputs, dim=0), (H, C)
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,
init_lstm_state, lstm)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
- 简洁实现
# 简洁实现
num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
三、深度循环神经网络
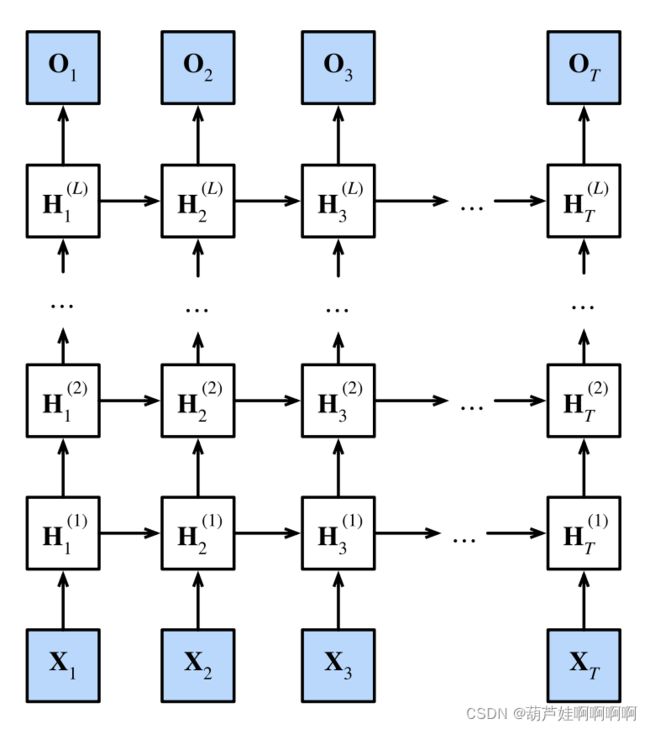
H t ( l ) = ϕ l ( H t ( l − 1 ) W x h ( l ) + H t − 1 ( l ) W h h ( l ) + b h ( l ) ) \pmb{H}_t^{(l)}=\phi_l(\pmb{H}_t^{(l-1)}\pmb{W}_{xh}^{(l)}+\pmb{H}_{t-1}^{(l)}\pmb{W}_{hh}^{(l)}+\pmb{b}_h^{(l)}) HHHt(l)=ϕl(HHHt(l−1)WWWxh(l)+HHHt−1(l)WWWhh(l)+bbbh(l))
O t = H t ( l ) W h q + b q \pmb{O}_t=\pmb{H}_t^{(l)}\pmb{W}_{hq}+\pmb{b}_q OOOt=HHHt(l)WWWhq+bbbq
import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
num_inputs = vocab_size
device = d2l.try_gpu()
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
num_epochs, lr = 500, 2
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
四、双向循环神经网络
H → t = ϕ ( X t W x h ( f ) + H → t − 1 W h h ( f ) + b h ( f ) ) H ← t = ϕ ( X t W x h ( b ) + H ← t − 1 W h h ( b ) + b h ( b ) ) \overrightarrow{\pmb H}_t=\phi(\pmb{X}_t\pmb{W}_{xh}^{(f)}+\overrightarrow{\pmb H}_{t-1}\pmb{W}_{hh}^{(f)}+\pmb{b}_h^{(f)})\\ \overleftarrow{\pmb H}_t=\phi(\pmb{X}_t\pmb{W}_{xh}^{(b)}+\overleftarrow{\pmb H}_{t-1}\pmb{W}_{hh}^{(b)}+\pmb{b}_h^{(b)}) HHHt=ϕ(XXXtWWWxh(f)+HHHt−1WWWhh(f)+bbbh(f))HHHt=ϕ(XXXtWWWxh(b)+HHHt−1WWWhh(b)+bbbh(b))
将前向隐状态 H → t \overrightarrow{\pmb H}_t HHHt和反向隐状态 H ← t \overleftarrow{\pmb H}_t HHHt拼接起来,得到输出层的隐状态 H t ∈ R n × 2 h \pmb H_t\in\mathbb R^{n \times2h} HHHt∈Rn×2h
H t = H → t ⊕ H ← t O t = H t W h q + b q \pmb{H}_t=\overrightarrow{\pmb H}_t\oplus\overleftarrow{\pmb H}_t\\ \pmb{O}_t=\pmb{H}_t\pmb{W}_{hq}+\pmb{b}_q HHHt=HHHt⊕HHHtOOOt=HHHtWWWhq+bbbq
-
注意:
双向循环神经网络一般不用于预测,因为预测的时候是看不到后面的