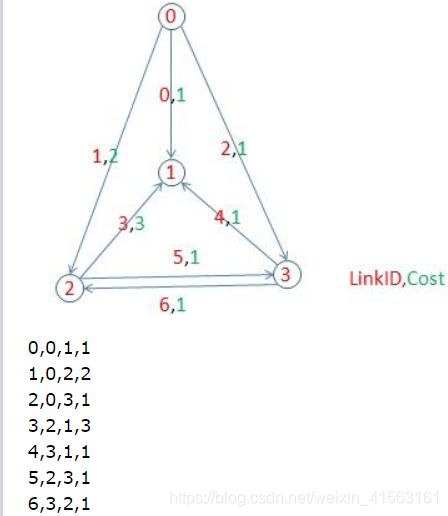
最短路径算法---有向图

                                最短路径算法---有向图、

 

 最短路算法

最常用的最短路算法是Dijkstra算法、A*算法、SPFA算法、Bellman-Ford算法和Floyd-Warshall算法,我们这里重点介绍并实现Dijkstra和SPFA,以及A*算法,

1.松弛技术（Relaxation）(非常重要)

松弛操作的原理是著名的定理：“三角形两边之和大于第三边”，在信息学中我们叫它三角不等式。所谓对结点i,j进行松弛，就是判定是否dis[j]>dis[i]+w[i,j]，如果该式成立则将dis[j]减小到dis[i]+w[i,j]，否则不动。

2.Dijkstra算法

解决最短路问题，最经典的算法是 Dijkstra算法，它是一种单源最短路算法，其核心思想是贪心算法(Greedy Algorithm)，Dijkstra算法由荷兰计算机科学家Dijkstra发现，这个算法至今差不多已有50年历史，但是因为它的稳定性和通俗性，到现在依然强健。另外，Dijkstra算法要求所有边的权值非负。
 

1) Dijkstra算法思想为：

设 G = (V, E) 是一个带权有向图，把图中顶点集合 V 分成两组，第一组为已求出最短路径的顶点集合（用 S 表示，初始时 S 中只有一个源点，以后每求得一条最短路径 , 就将其加入到集合 S 中，直到全部顶点都加入到 S 中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用 U 表示），按最短路径长度的递增次序依次把第二组的顶点加入 S 中。在加入的过程中，总保持从源点 v 到 S 中各顶点的最短路径长度不大于从源点 v 到 U 中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S 中的顶点的距离就是从 v 到此顶点的最短路径长度，U 中的顶点的距离，是从 v 到此顶点只包括 S 中的顶点为中间顶点的当前最短路径长度。

2)算法核心步骤如下:

    a. 将所有顶点分为两部分：已知最短路程的顶点集合P和未知最短路径的顶点集合Q。最开始，已知最短路径的顶点集合P中只有源点一个顶点。我们这里用一个isVisited数组来记录哪些顶点再集合P中。例如对于某个顶点i，如果isVisited[i]为1则表示这个顶点再集合P中，如果isVisited[i]为0则表示这个顶点再集合Q中。
    b. 设置源点s到自己的最短路径为0即 dis[s]=0。若存在有源点能直接到达的顶点i，则把dis[i]设为w[s][i]。同时把所有其他（源点不能直接到达的）顶点的最短路径设为∞。
    c. 在集合Q的所有顶点中选择一个离源点s最近的顶点u（即dis[u]最小）加入到集合P。并考察所有以点u为起点的边，对每一条边进行松弛操作。例如存在一条从u到v的边，那么可以通过将u->v添加到尾部来拓展一条从s到v的路径，这条路径的长度时dis[u]+w[u][v]。如果这个值比目前已知的dis[v]的值要小，我们可以用新值来替代当前dis[v]中的值。
    d. 重复第3步，如果集合Q为空，算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。

补充:dis数组用来记录起点到所有顶点的距离,Path[]数组，Path[i]表示从S到i的最短路径中，结点i之前的结点的编号。注意，是“之前”，不是“之后”。最短路径算法的核心思想成为“松弛”，原理是三角形不等式,我们只需要在借助结点u对结点v进行松弛的同时，标记下Path[v] = u，记录的工作就完成了。
 

算法实现思路 

拓扑排序，其实就是寻找一个入度为0的顶点，该顶点是拓扑排序中的第一个顶点序列，将之标记删除，然后将与该顶点相邻接的顶点的入度减1，再继续寻找入度为0的顶点，直至所有的顶点都已经标记删除或者图中有环。

从上可以看出，关键是寻找入度为0的顶点。

一种方式是遍历整个图中的顶点，找出入度为0的顶点，然后标记删除该顶点，更新相关顶点的入度，由于图中有V个顶点，每次找出入度为0的顶点后会更新相关顶点的入度，因此下一次又要重新扫描图中所有的顶点。故时间复杂度为O(V^2)

由于删除入度为0的顶点时，只会更新与它邻接的顶点的入度，即只会影响与之邻接的顶点。但是上面的方式却遍历了图中所有的顶点的入度。

改进的另一种方式是：先将入度为0的顶点放在栈或者队列中。当队列不空时，删除一个顶点v，然后更新与顶点v邻接的顶点的入度。只要有一个顶点的入度降为0，则将之入队列。此时，拓扑排序就是顶点出队的顺序。该算法的时间复杂度为O（V+E）

拓扑排序方法的实现

该算法借助队列来实现时，感觉与 二叉树的 层序遍历算法很相似啊。说明这里面有广度优先的思想。

第一步：遍历图中所有的顶点，将入度为0的顶点 入队列。

第二步：从队列中出一个顶点，打印顶点，更新该顶点的邻接点的入度(减1)，如果邻接点的入度减1之后变成了0，则将该邻接点入队列。

第三步：一直执行上面 第二步，直到队列为空。

public void topoSort() throws Exception{
        int count = 0;//判断是否所有的顶点都出队了,若有顶点未入队(组成环的顶点)，则这些顶点肯定不会出队
        
        Queue queue = new LinkedList<>();// 拓扑排序中用到的栈,也可用队列.
        //扫描所有的顶点,将入度为0的顶点入队列
        Collection vertexs = directedGraph.values();
        for (Vertex vertex : vertexs)
            if(vertex.inDegree == 0)
                queue.offer(vertex);
        //度为0的顶点出队列并且更新它的邻接点的入度
        while(!queue.isEmpty()){
            Vertex v = queue.poll();
            System.out.print(v.vertexLabel + " ");//输出拓扑排序的顺序
            count++;
            for (Edge e : v.adjEdges) 
                if(--e.endVertex.inDegree == 0)
                    queue.offer(e.endVertex);
        }
        if(count != directedGraph.size())
            throw new Exception("Graph has circle");
    }

 

第7行for循环：先将图中所有入度为0的顶点入队列。

第11行while循环：将入度为0的顶点出队列，并更新与之邻接的顶点的入度，若邻接顶点的入度降为0，则入队列（第16行if语句）。

第19行if语句判断图中是否有环。因为，只有在每个顶点出队时，count++。对于组成环的顶点，是不可能入队列的，因为组成环的顶点的入度不可能为0（第16行if语句不会成立）.

因此，如果有环，count的值 一定小于图中顶点的个数。

完整代码实现

import java.util.Collection;
import java.util.LinkedHashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Queue;

/*
 * 用来实现拓扑排序的有向无环图
 */
public class DirectedGraph {

    private class Vertex{
        private String vertexLabel;// 顶点标识
        private List adjEdges;
        private int inDegree;// 该顶点的入度

        public Vertex(String verTtexLabel) {
            this.vertexLabel = verTtexLabel;
            inDegree = 0;
            adjEdges = new LinkedList();
        }
    }

    private class Edge {
        private Vertex endVertex;

        // private double weight;
        public Edge(Vertex endVertex) {
            this.endVertex = endVertex;
        }
    }

    private Map directedGraph;

    public DirectedGraph(String graphContent) {
        directedGraph = new LinkedHashMap();
        buildGraph(graphContent);
    }

    private void buildGraph(String graphContent) {
        String[] lines = graphContent.split("\n");
        Vertex startNode, endNode;
        String startNodeLabel, endNodeLabel;
        Edge e;
        for (int i = 0; i < lines.length; i++) {
            String[] nodesInfo = lines[i].split(",");
            startNodeLabel = nodesInfo[1];
            endNodeLabel = nodesInfo[2];
            startNode = directedGraph.get(startNodeLabel);
            if(startNode == null){
                startNode = new Vertex(startNodeLabel);
                directedGraph.put(startNodeLabel, startNode);
            }
            endNode = directedGraph.get(endNodeLabel);
            if(endNode == null){
                endNode = new Vertex(endNodeLabel);
                directedGraph.put(endNodeLabel, endNode);
            }
            
            e = new Edge(endNode);//每读入一行代表一条边
            startNode.adjEdges.add(e);//每读入一行数据,起始顶点添加一条边
            endNode.inDegree++;//每读入一行数据,终止顶点入度加1
        }
    }

    public void topoSort() throws Exception{
        int count = 0;
        
        Queue queue = new LinkedList<>();// 拓扑排序中用到的栈,也可用队列.
        //扫描所有的顶点,将入度为0的顶点入队列
        Collection vertexs = directedGraph.values();
        for (Vertex vertex : vertexs)
            if(vertex.inDegree == 0)
                queue.offer(vertex);
        
        while(!queue.isEmpty()){
            Vertex v = queue.poll();
            System.out.print(v.vertexLabel + " ");
            count++;
            for (Edge e : v.adjEdges) 
                if(--e.endVertex.inDegree == 0)
                    queue.offer(e.endVertex);
        }
        if(count != directedGraph.size())
            throw new Exception("Graph has circle");
    }
}

FileUtil.java负责从文件中读取图的信息。将文件内容转换成 第一点 中描述的字符串格式。--该类来源于网络

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.Closeable;
import java.io.File;
import java.io.FileReader;
import java.io.FileWriter;
import java.io.IOException;

public final class FileUtil
{
    /** 
     * 读取文件并按行输出
     * @param filePath
     * @param spec 允许解析的最大行数， spec==null时，解析所有行
     * @return
     * @author
     * @since 2016-3-1
     */
    public static String read(final String filePath, final Integer spec)
    {
        File file = new File(filePath);
        // 当文件不存在或者不可读时
        if ((!isFileExists(file)) || (!file.canRead()))
        {
            System.out.println("file [" + filePath + "] is not exist or cannot read!!!");
            return null;
        }

        BufferedReader br = null;
        FileReader fb = null;
        StringBuffer sb = new StringBuffer();
        try
        {
            fb = new FileReader(file);
            br = new BufferedReader(fb);

            String str = null;
            int index = 0;
            while (((spec == null) || index++ < spec) && (str = br.readLine()) != null)
            {
                sb.append(str + "\n");
//                System.out.println(str);

            }
        }
        catch (IOException e)
        {
            e.printStackTrace();
        }
        finally
        {
            closeQuietly(br);
            closeQuietly(fb);
        }

        return sb.toString();
    }
    /** 
     * 写文件
     * @param filePath 输出文件路径
     * @param content 要写入的内容
     * @param append 是否追加
     * @return
     * @author s00274007
     * @since 2016-3-1
     */
    public static int write(final String filePath, final String content, final boolean append)
    {
        File file = new File(filePath);
        if (content == null)
        {
            System.out.println("file [" + filePath + "] invalid!!!");
            return 0;
        }

        // 当文件存在但不可写时
        if (isFileExists(file) && (!file.canRead()))
        {
            return 0;
        }

        FileWriter fw = null;
        BufferedWriter bw = null;
        try
        {
            if (!isFileExists(file))
            {
                file.createNewFile();
            }

            fw = new FileWriter(file, append);
            bw = new BufferedWriter(fw);

            bw.write(content);
        }
        catch (IOException e)
        {
            e.printStackTrace();
            return 0;
        }
        finally
        {
            closeQuietly(bw);
            closeQuietly(fw);
        }

        return 1;
    }

    private static void closeQuietly(Closeable closeable)
    {
        try
        {
            if (closeable != null)
            {
                closeable.close();
            }
        }
        catch (IOException e)
        {
        }
    }

    private static boolean isFileExists(final File file)
    {
        if (file.exists() && file.isFile())
        {
            return true;
        }

        return false;
    }
}

测试类

public class TestTopoSort {
    public static void main(String[] args) {
        String graphFilePath;
        if(args.length == 0)
            graphFilePath = "F:\\xxx";
        else
            graphFilePath = args[0];
        
        String graphContent = FileUtil.read(graphFilePath, null);//从文件中读取图的数据
        DirectedGraph directedGraph = new DirectedGraph(graphContent);
        try{
            directedGraph.topoSort();
        }catch(Exception e){
            System.out.println("graph has circle");
            e.printStackTrace();
        }
    }
}

参考链接

https://blog.csdn.net/xqhadoop/article/details/69665823