粒子群算法——王者荣耀的视野共享辅助决策的底层原理

本文为北海的数模课程学习笔记，课程出自微信公众号：数学建模BOOM。

求赞！求收藏！求关注！

模型简介

粒子群算法（Particle Swarm Optimization, PSO）

基本信息

若鸟群太大/太小

若鸟群（粒子）太大：

1. 计算开销增加： 粒子的数量增加会导致算法的计算开销增加，因为每个粒子都需要更新位置和速度，并计算适应度值。

2. 收敛速度变慢： 当粒子数量很多时，群体中的信息交流和协作会变得更加复杂，导致收敛速度变慢。算法可能需要更多的迭代次数才能找到接近最优解的解决方案。

若鸟群（粒子）太小：

1. 收敛速度快但易陷入局部最优： 少量的粒子会导致群体信息交流简单，可能会导致算法收敛速度加快，但容易陷入局部最优解。

2. 不稳定性增加： 粒子数量少可能导致算法的性能在不同问题上表现不稳定，因为少量粒子的搜索策略可能无法适应多样的问题特性。

算法思路

算法优缺点

• 优点：收敛快，简单易实现，几乎任何寻优问题都能用其求解

• 缺点：局部搜索能力较差，搜索精度不够高

改进办法：

适用赛题

多目标优化问题

充电站布局优化（美赛）、背包问题

当目标函数复杂、变量多（维度高），传统求解方法速度很慢

粒子群算法的最大优点： 快 ！（尤其是高维度且目标函数复杂的优化问题）

各种寻优问题

直接求解，或为这些问题的模型提供初始值或参数优化

典型例题与原理讲解

题目描述

步骤1：参数初始化。随机生成N只鸟。

步骤2：根据Chaffer函数计算初始适应度

步骤3：求初始全局最优解

        个体（personal）最优解pbest：第i只鸟去过的适应度最高的位置

        pbest中的最优解为全局（global）最优解gbest

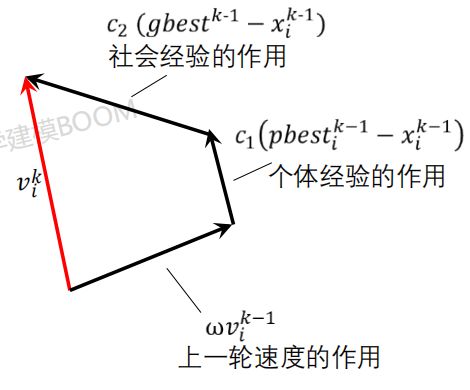
步骤4：更新粒子速度

        第k次迭代后的速度=W*当前速度+C1*向pbest的方向移动+C2*向gbest的方向移动

       （位移=速度*时间，算法中速度默认为1，因此位移=速度）

步骤5：更新位置并求适应度

        新位置=当前位置+位移量

步骤6：更新pbest和gbest

步骤7：迭代与终止

        迭代：重复步骤4~6

        终止：输出最后的gbest和对应适应度

代码求解

Schaffer函数：
求解, 在[0,10]范围内Schaffer的最小值。

函数可视化

clear,clc,close all;
% 定义变量
x1 = (-10:0.05:10);
x2 = (-10:0.05:10);
[X1,X2] = meshgrid(x1,x2);% 建立网格，X1是每个格点的横坐标，X2是每个格点的纵坐标
[m,n] = size(X1);

% 把这个函数画出来，先求出函数值
for i = 1:m
    for j = 1:n
        f(i,j) = PSO_Schaffer(X1(i,j),X2(i,j));
    end
end
mesh(X1,X2,f);    % 创建schaffer的三维曲面图

算法初始化

%粒子群算法中的三个参数
w=0.5;      % 惯性
c1 = 1;     % 个体经验
c2 = 1;     % 社会经验

maxg = 200;   % 迭代次数，太少解不稳定，太大浪费时间。越复杂的表达式，可设的越大
N = 100;      % 粒子数，一般50到1000都可以，若函数自变量范围越大，可把粒子数设的越多些

Vmax = 1;       % 速度范围，增加稳定性
Vmin = -1;     
Xmax = 10;      % 变量取值范围，根据定义域取
Xmin = -10;
dim = 2;        % 适应度函数的维数，即函数表达式的自变量个数

% 初始化N个粒子
for i=1:N
    location(i,:)=Xmax*rands(1,dim);    % 初始化坐标；rands求得-1到1之间的随机数
    V(i,:)=Vmax*rands(1,dim);           % 初始化速度
    fitness(i)=PSO_Schaffer(location(i,1),location(i,2));     % 相应的适应度
end

% 个体最优解和群体最优解
% fitnessgbest是最优解对应的函数值，bestindex是最优解对应的下标（即相应鸟的编号）
[fitnessgbest,bestindex]=min(fitness);       % 本题求最小值；fitnessgbest是全局最优解对应的适应度
gbest=location(bestindex,:);   % 全局最优解
pbest=location;                % 所有鸟的个体最优解，这是初始化，还没开始迭代
fitnesspbest=fitness;          % 所有鸟的个体最优解对应的适应度

迭代寻优

迭代maxg轮，每轮更新N个粒子；
也可写成while循环，终止条件设为“连续10次全体最优解变化小于0.01”之类的。

for i=1:maxg
    % 一轮迭代中，对每一个粒子进行处理
    for j=1:N
        % 根据惯性、个体最优pbest和群体最优gbest更新速度
        V(j,:) = w*V(j,:) + c1*(pbest(j,:) - location(j,:)) + c2*(gbest - location(j,:)); 
        % 限制速度不能过大
        for k = 1:dim
            if V(j,k) > Vmax
                V(j,k) = Vmax;
            elseif V(j,k) < Vmin
                V(j,k) = Vmin;
            end
        end
        
        % 更新位置
        location(j,:) = location(j,:) + V(j,:); 
        % 限制位置不能超过边界
        for k = 1:dim
            if location(j,k) > Xmax
                location(j,k) = Xmax;
            elseif location(j,k) < Xmin
                location(j,k) = Xmin;
            end
        end
        
        %更新第j个粒子的适应度值
        fitness(j) = PSO_Schaffer(location(j,1),location(j,2)); 
    end

    for j = 1:N
        % 更新个体最优解
        if fitnesspbest(j) > fitness(j)
            pbest(j,:) = location(j,:);
            fitnesspbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitnessgbest > fitness(j)
            gbest = location(j,:);
            fitnessgbest = fitness(j);
        end
    end 
    yy(i) = fitnessgbest;    
end
%% 结果分析
figure;
plot(yy)
title('群体最优适应度','fontsize',12);
xlabel('迭代代数','fontsize',18);ylabel('适应度','fontsize',18);

function Y = PSO_Schaffer(x1,x2)
    temp1 = x1^2 + x2^2;
    temp2 = sin(sqrt(temp1));
    Y = 0.5 + (temp2^2 - 0.5)/((1+0.001*temp1)^2);
end