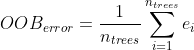从根到叶:随机森林模型的深入探索
一、说明
经验丰富的数据科学家通常对他们的数据集有一种直观的感觉——引导他们找到正确的算法和正确的参数的第六感。虽然这看起来像是神秘的魔法,但这只是多年应用和理解这些模型经验的结果。在本博客中,我们将介绍随机森林算法的核心元素,以便它不仅易于理解,而且易于在数据科学项目中应用。因此,无论您是希望掌握随机森林的数据爱好者,还是寻求复习更深入见解的从业者,这个博客都是您的指南针。
“随机森林是一种集成机器学习方法,它结合了多个决策树以产生更准确和稳健的预测。”
对于大多数情况来说这是一个恰当的描述,但我们正在寻找更多的东西。您将在下面找到代码和说明,以了解操纵算法的关键参数将如何影响模型的性能。
二、设置场景
通常,在进入建模阶段之前,您已经对数据集进行了清理和探索性数据分析。由此,您将对数据如何变化以及与因变量的关系有一个扎实的了解,这反过来又会根据您对这些模型如何工作的理解,为哪些模型值得探索提供一些指导。
在本博客中,我们将使用经典的 Iris 玩具数据集,并向变量中注入一些噪声,以便我们可以看到优化模型参数的价值:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_score
# 加载 Iris 数据集
data = load_iris()
X = data.data
y = data.target
# 向特征中引入噪声
Noise_factor = 0.5
X_noisy = X + Noise_factor * np.random.randn(*X.shape)
# 将数据集分割为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_noisy) , y, test_size= 0.3 , random_state= 42 )三、树木数量
让我们从要调整的明显参数开始,n_estimators即构建模型时要考虑的树的数量。随机森林模型是一种集成方法,将生成多个树,组合结果以形成一个输出。这里的目标是在不增加偏差的情况下减少方差,以大数定律为基础:
你拥有的树越多,你就越能相信平均预测更接近事实,其中Y ₁ 是iᵗʰ树的预测。与容易过度拟合的决策树相比,尤其是在深度时,随机森林模型可以利用自举样本方法来确保没有一棵树过度专业化,从而允许通用的最终模型。
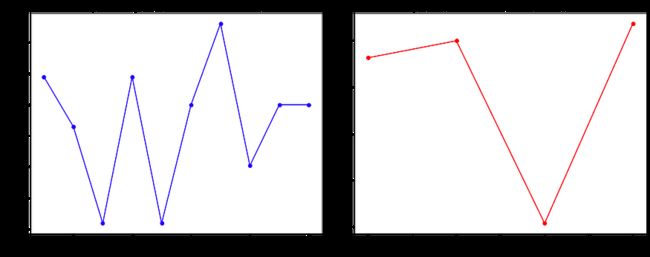
袋外 (OOB) 错误:由于每棵树都是可用数据的子集,因此我们可以使用“袋外”样本来验证和量化树木的质量。随着树数量的增加,OOB 误差将趋于稳定,这证明我们的模型可能在未见过的数据上表现良好。下面的方程说明了每个iᵗʰ树的误差e如何减小的高级视图。
特征重要性:可解释性是构建数据科学模型的必备要素。增加树的数量可以更可靠地了解哪些特征驱动预测,并减少 OOB 错误。
计算与性能权衡:读完本文后,您可能会想将树的数量设置为较高的值,因为这将为构建更好的模型提供统计优势,但这样做也会导致大量的计算负载。虽然增加更多树木会带来增量效益,但随着总数量的增加,这种效益将会减少。我们可以从下面的例子中看到这一点:
# Define a range for the number of trees
n_trees_range = list(range(1, 301))
# Placeholder for precision results
precision = []
# Train and test random forests for different numbers of trees
for n_trees in n_trees_range:
clf = RandomForestClassifier(n_estimators=n_trees, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
precision.append(precision_score(y_test, y_pred, average='weighted'))
# Plot the results
plt.figure(figsize=(10,6))
plt.plot(n_trees_range, precision, color='green')
plt.xlabel('Number of Trees')
plt.ylabel('Precision')
plt.title('Impact of Number of Trees on Model Performance')
plt.show() 从上面的分析我们可以看到,当n_estimators > 50我们的精度得到边际提升时,它确实开始稳定下来。
我的主要收获:
- 欠拟合:树数较少的模型可能无法捕获数据中的所有关系和模式,从而导致欠拟合
- 稳定性:随着树木数量的增加,您可能会观察到性能的提高,但在某一点后会稳定下来。
- 收益递减:在某一点之后,增加生成的树数量所获得的收益将是最小的,这样做可能只会导致计算效率更高的解决方案。
四、树深度
本质上,树深度是一棵树可以具有的级别(节点)数量,与前面调整可用树数量的示例不同,增加树深度可能会对模型的可解释性、复杂性和计算负载产生不利影响。不合理地增加该参数的值会增加模型过度拟合的风险。
树深度的影响:树的深度与其复杂性成正比,因为更深的树将有更多的节点,因此有更多的决策边界。虽然这可能允许模型捕获数据中更复杂的模式,但模型开始过度拟合或变得更难以解释的风险更大。平衡树的深度和树的数量对于减少过度拟合的可能性很重要,因为后者会在一定程度上减轻过度拟合的可能性。
平衡偏差和方差:相对于具有低偏差和高方差的较深树,浅树(有时称为“树桩”)在高偏差和低方差下更容易解释。考虑到这一点,随机森林模型中的树显然存在一个最佳级别,我们可以通过以下示例来强调这一点:
# Define a range for maximum depth of the tree
max_depth_range = list(range(1, 21))
# Placeholder for precision results
precision = []
# Train and test random forests for different tree depths
for max_depth in max_depth_range:
clf = RandomForestClassifier(max_depth=max_depth, n_estimators=50, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
precision.append(precision_score(y_test, y_pred, average='weighted'))
# Plot the results
plt.figure(figsize=(10,6))
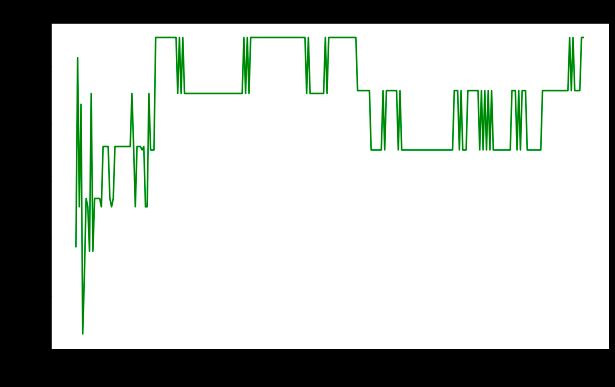
plt.plot(max_depth_range, precision, color='purple')
plt.xlabel('Maximum Depth of Tree')
plt.ylabel('Precision')
plt.title('Impact of Tree Depth on Model Performance')
plt.show()在这里,我们可以看到精度随着树深度增加到一定水平然后下降,这表明模型对数据集中的噪声可能存在过度拟合。
我的主要收获:
- 欠拟合:对于浅树,我们的模型可能不够复杂,无法理解我们希望它从数据中找到的模式,从而导致欠拟合。
- 过度拟合:如果我们不限制深度并允许树生长,模型可能会开始适应训练数据中的噪声,从而导致过度拟合
- 最佳深度:我们的模型将有一个最佳深度,可以在欠拟合和过度拟合之间取得平衡,您需要通过交叉验证等技术来探索和验证该深度。
五、加权分数和特征数量
变量:加权分数和特征数量是随机森林算法中最容易被忽视的两个参数,但它们在正则化(减少过度拟合)和提高生成的树之间的多样性方面具有巨大的价值。
加权分数表示节点成为叶子节点所需的最小样本权重之和的阈值。例如,给定样本的总权重W和加权分数ω,叶节点必须满足以下条件:
![]()
随着加权分数的增加,我们通常会观察到更大的正则化,这也可以防止树木生长得更深。如果您的数据集不平衡,通过确保少数类样本在叶节点中得到充分表示,此参数也非常有用。
当我们的树被构建并且节点被分割时,算法将考虑特征的子集。该子集的大小可以使用参数进行配置:特征数量。增加此值将在树之间引入更多的变异性,这对于鲁棒性和泛化性都很重要,但是它可能会导致树过于复杂,从而可能与我们的训练数据过度拟合。仅出于这个原因,适当配置此值就很重要,但您还会注意到您的模型对计算的要求越来越低,尤其是当您的数据集包含许多维度时。如上所述,让我们探讨一下改变这些参数的影响:
# Varying max_samples (Weighted Fraction)
fractions = np.linspace(0.1, 1.0, 10) # From 10% to 100%
precision_fraction = []
for fraction in fractions:
clf = RandomForestClassifier(max_samples=fraction, n_estimators=50, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
precision_fraction.append(precision_score(y_test, y_pred, average='weighted'))
# Varying max_features (Number of Features)
num_features = list(range(1, X_train.shape[1] + 1))
precision_features = []
for n_features in num_features:
clf = RandomForestClassifier(max_features=n_features, n_estimators=50, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
precision_features.append(precision_score(y_test, y_pred, average='weighted'))
# Plot the results
fig, ax = plt.subplots(1, 2, figsize=(15,6))
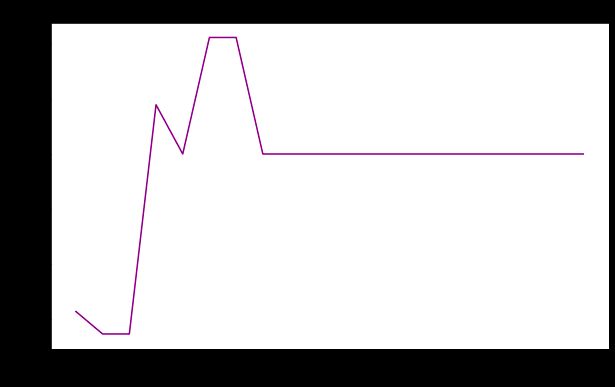
ax[0].plot(fractions, precision_fraction, color='blue', marker='o')
ax[0].set_xlabel('Fraction of Samples (max_samples)')
ax[0].set_ylabel('Precision')
ax[0].set_title('Impact of Weighted Fraction on Model Performance')
ax[1].plot(num_features, precision_features, color='red', marker='o')
ax[1].set_xlabel('Number of Features (max_features)')
ax[1].set_ylabel('Precision')
ax[1].set_title('Impact of Number of Features on Model Performance')
plt.tight_layout()
plt.show()我的主要收获:
- 加权分数:如果该值太小,我们可能无法捕获足够的数据多样性,从而导致模型过度拟合。增加这个分数可以帮助更好地找到真正的下划线模式,特别是在我们的类别不平衡的情况下。
- 特征数量:特征数量非常少可能会导致节点分裂而错过重要特征,进而可能导致过度拟合,同时考虑到所有特征不仅计算成本高,而且可能导致噪声扭曲模型发现的关系。
六、种植具有最大叶节点的树
该参数控制我们构建的树中叶节点的最大数量(终端节点的数量)。限制该值可以驱动“贪婪算法”方法来形成树,其中首先以自上而下的方式生长树,进行最有利的分割。下面列出了此参数的主要优点(优点和缺点):
优点:
- 控制过度拟合:通过减少叶节点的数量,随机森林将生成更简单、易于解释的树。这种复杂性的降低也意味着树不太可能适应训练数据上的噪声,因此您可以将其视为正则化的隐式形式。
- 计算效率:对上述一点的补充,可能非常明显,但由于树中的节点较少,我们能够更快地构建模型。这种效果与我们的树木数量参数相结合。
缺点:
- 潜在的欠拟合:如果叶节点的最大数量设置得太低,则模型将过于通用,并且无法捕获数据中真正的下划线模式。
- 粒度损失:使树过于简单可能会导致模型无法捕获数据中更深的树可以捕获的更复杂的关系。
让我们通过 Python 示例来形象化这一点:
# Define a range for max_leaf_nodes
max_leaf_nodes_range = list(range(2, 51)) # Starting from 2 (smallest possible tree) to 50 as an example
# Placeholder for precision results
precision = []
# Train and test random forests for different max_leaf_nodes
for max_leaf_nodes in max_leaf_nodes_range:
clf = RandomForestClassifier(max_leaf_nodes=max_leaf_nodes, n_estimators=50, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
precision.append(precision_score(y_test, y_pred, average='weighted'))
# Plot the results
plt.figure(figsize=(10,6))
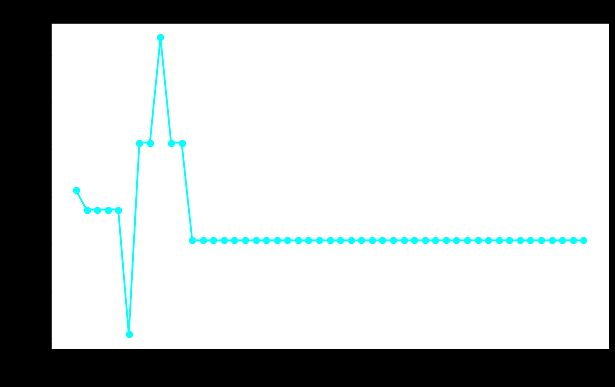
plt.plot(max_leaf_nodes_range, precision, color='cyan', marker='o')
plt.xlabel('Maximum Leaf Nodes')
plt.ylabel('Precision')
plt.title('Impact of Maximum Leaf Nodes on Model Performance')
plt.show()配置或优化最大叶节点的值时,考虑其他参数非常重要。
我的主要收获:
欠拟合:最大叶节点数量非常少,树受到很大限制,这可能会导致欠拟合。
过度拟合:如果将最大叶节点设置得太高,树可能会变得更加复杂,并且可能会适应训练数据中的噪声(导致过度拟合)。
最佳叶节点:将有许多叶节点(或范围)提供最佳性能,平衡欠拟合和过拟合。
七、标准和最小杂质减少
树的构建受两个关键原则的控制:分裂准则和最小杂质减少阈值。这些元素确保在节点分裂时做出有意义且富有洞察力的决策。
分裂标准:
该度量表示分割的整体质量,即特征将数据划分为同质子集的程度。随机森林的大多数实现都提供两种定义分割标准的方法:基尼杂质和熵。
基尼杂质 ( G ):最简单的形式表示以p ᵢ 的概率随机选择数据集的任何元素时被错误标记的频率。
![]()
熵 ( H ):节点处不确定性和无序性的度量,节点被分类为i类的概率为p ᵢ 。
![]()
这两种方法都旨在最大化类别同质性,但是您可能会发现基尼系数的计算速度更快,因为它不涉及对数运算。另一方面,熵通常倾向于使头发更加平衡。
最小杂质减少量:
在进行分割之前,模型需要确定是否有必要。最小杂质减少量是考虑的阈值,表示考虑分裂节点所需的杂质减少量。随机森林算法只会考虑分割,如果这样做会使整体杂质减少 Δ I:
其中I是杂质,N是父节点的样本总数,N左下标和右下标分别是左分支和右分支的样本数量。
较高的最小杂质减少量 Δ I可以减少模型构建过程中的方差,从而使模型对训练数据中的噪声不太敏感。然而,如果所需的分割太少(以对数据内的模式进行完全建模)不满足阈值,它也可能使模型产生偏差。
和以前一样,下面的代码用于查看更改这些参数如何改变模型对数据集的执行效果:
# Define a range of impurity decrease thresholds
thresholds = np.linspace(0, 0.5, 50)
# Placeholder for precision results
precision_gini = []
precision_entropy = []
# Train and test decision trees for different impurity thresholds
for threshold in thresholds:
for criterion, accuracies in [('gini', precision_gini), ('entropy', precision_entropy)]:
clf = RandomForestClassifier(criterion=criterion, min_impurity_decrease=threshold)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracies.append(precision_score(y_test, y_pred, average='weighted'))
# Plot the results
plt.figure(figsize=(10,6))
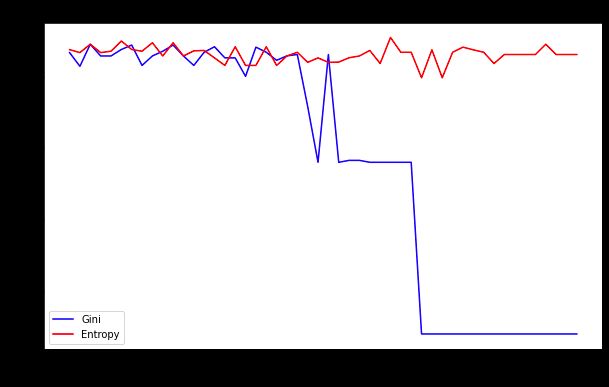
plt.plot(thresholds, precision_gini, label='Gini', color='blue')
plt.plot(thresholds, precision_entropy, label='Entropy', color='red')
plt.xlabel('Min Impurity Decrease')
plt.ylabel('Precision')
plt.legend()
plt.title('Impact of Node Impurity on Model Performance')
plt.show()我的主要收获:
- min_impurity_decrease 值较高可能会使树过于简单(欠拟合),因为会进行较少的分割。
- 值太低可能会使树过于复杂,可能会过度拟合训练数据。
八、最小成本复杂性修剪
到目前为止,我们已经探索了许多参数的复杂性,目的是确保最终模型足够通用,但也足够复杂以捕获数据中真正的底层结构。成本复杂性修剪是通过确保树不会长得太深来保持泛化的另一种方法。为了便于解释其工作原理,我们将成本复杂度函数表示为:
其中R(T)是树T的总误分类率,∣ T ∣ 终端节点的数量以及α我们的复杂度参数。修剪方法遵循以下两步过程:
- 对于每个终端节点 t,计算复杂度参数:
以R(Tₜ)作为子树Tₜ的误分类率,在t 处腐烂。
2. 修剪子树Tₜ,其中αₜ处于最小值。
重复此过程直到找到最佳子树。应注意选择正确的复杂性参数αₜ ,因为值太高可能会引入偏差和欠拟合模型,而αₜ过低可能会导致模型对数据过度拟合。应应用交叉验证来确定适当的阈值,以下是改变此参数如何影响我们的模型的示例:
# Define a range for ccp_alpha values. For demonstration purposes, we'll consider a linear space.
# In real scenarios, you may want to fine-tune this range based on the specific dataset.
ccp_alpha_range = np.linspace(0, 0.04, 50)
# Placeholder for precision results
precision = []
# Train and test random forests for different ccp_alpha values
for ccp_alpha in ccp_alpha_range:
clf = RandomForestClassifier(ccp_alpha=ccp_alpha, n_estimators=50, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
precision.append(precision_score(y_test, y_pred, average='weighted'))
# Plot the results
plt.figure(figsize=(10,6))
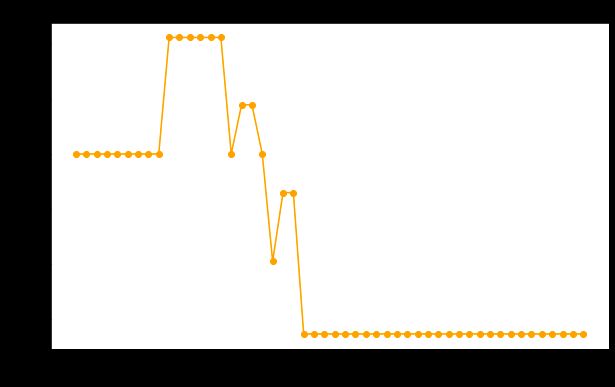
plt.plot(ccp_alpha_range, precision, color='orange', marker='o')
plt.xlabel('CCP Alpha')
plt.ylabel('Precision')
plt.title('Impact of Cost-Complexity Pruning (ccp_alpha) on Model Performance')
plt.show()我的主要收获:
剪枝不足:ccp_alpha 为 0 时,不应用剪枝,可能导致大树过度拟合。
过度剪枝:非常高的 ccp_alpha 值将导致过度剪枝,使模型过于简单并可能欠拟合。
最优剪枝:会有一个 ccp_alpha 值(或范围)提供最佳性能,实现树复杂性和泛化性之间的平衡。
九、概括
在本博客中,我们介绍了随机森林模型中的一系列不同参数,重点介绍了它们如何影响模型性能。目的是通过数学和 Python 示例将其中一些元素带入生活,从而能够在真实数据上有效使用随机森林。作为将所有这些结合在一起的最后一步,让我们以另一个示例结束,该示例将展示如何使用网格搜索算法和交叉验证来找到模型的最佳参数集。我们将从上面的图形示例中确定的内容来限制限制并定义参数网格的范围。这很重要,因为网格搜索和交叉验证算法的计算要求很高,因此我们需要对要探索的参数空间进行选择性。还有其他方法(例如贝叶斯优化)可以帮助加快寻找最佳参数集的过程。
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import precision_score, make_scorer
import json
# Define a parameter grid to search
param_grid = {
'n_estimators': [50, 100, 150],
'criterion': ['gini', 'entropy'],
'max_depth': [None, 5, 7, 10],
'max_samples': [0.6, 0.7, 0.8],
'max_features': [1, 2, 3, 4],
'max_leaf_nodes': [None, 10, 12, 14],
'min_impurity_decrease': [0.1, 0.2, 0.3],
'ccp_alpha': [0.01, 0.015, 0.02]
}
# Create a base model
clf = RandomForestClassifier(random_state=42)
# Define the scoring function
precision_scorer = make_scorer(precision_score, average='weighted')
# Instantiate the grid search model
grid_search = GridSearchCV(estimator=clf, param_grid=param_grid,
cv=5, n_jobs=-1, scoring=precision_scorer, verbose=2)
# Fit the grid search to the data
grid_search.fit(X_train, y_train)
# Getting the best parameters and score
best_params = grid_search.best_params_
best_score = grid_search.best_score_
print("Best parameters:", json.dumps(best_params, indent=1))
print("Best precision score:", best_score)Best parameters: {
"ccp_alpha": 0.01,
"criterion": "gini",
"max_depth": null,
"max_features": 2,
"max_leaf_nodes": null,
"max_samples": 0.6,
"min_impurity_decrease": 0.3,
"n_estimators": 50
}
Best precision score: 0.906669758812616