Dropout层、BN层、Linear层 & 神经网络的基本组成

图1 卷积网络中的 layers

---

承接上三篇博客：卷积层(空洞卷积对比普通卷积)、激活函数层、池化层 & 感受野

---

目录

（1）Dropout层

（2）BN层（BatchNormal）

（3）全连接层

---

（1）Dropout层

在深度学习中，当参数过多而训练样本又比较少时，模型容易产生过拟合现象。过拟合是很多深度学习乃至机器学习算法的通病，具体表现为在训练集上预测准确率高，而在测试集上准确率大幅下降。2012 年，Hinton等人提出了Dropout算法，可以比较有效地缓解过拟合现象的发生，起到一定正则化的效果。

Dropout的基本思想如图2 所示，在训练时，每个神经元以概率 p 保留，即以 1-p 的概率停止工作，每次前向传播保留下来的神经元都不同，这样可以使得模型不太依赖于某些局部特征，泛化性能更强。在测试时，为了保证相同的输出期望值，每个参数还要乘以p。当然还有另 外一种计算方式称为Inverted Dropout，即在训练时将保留下的神经元乘以1/p，这样测试时就不需要再改变权重。

图2 Dropout与普通网络的对比

至于Dropout为什么可以防止过拟合，可以从以下3个方面解释。

• 多模型的平均：不同的固定神经网络会有不同的过拟合，多个取平均则有可能让一些相反的拟合抵消掉，而Dropout每次都是不同的神经元失活，可以看做是多个模型的平均，类似于多数投票取胜的策略。 
• 减少神经元间的依赖：由于两个神经元不一定同时有效，因此减少了特征之间的依赖，迫使网络学习有更为鲁棒的特征，因为神经网络不应该对特定的特征敏感，而应该从众多特征中学习更为共同的规律， 这也起到了正则化的效果。
• 生物进化：Dropout类似于性别在生物进化中的角色，物种为了适应环境变化，在繁衍时取雄性和雌性的各一半基因进行组合，这样可以适应更复杂的新环境，避免了单一基因的过拟合，当环境发生变化时也不至于灭绝。

Dropout被广泛应用到全连接层中，一般保留概率设置为0.5。

Dropout 代码：

import torch
import torch.nn as nn
from torch import autograd

# ================================================================= #
# # Dropout Layers
# class torch.nn.Dropout(p=0.5, inplace=False)
# 随机将输入张量中部分元素设置为 0。对于每次前向调用，被置 0 的元素都是随机的。
# 参数：
# p - 将元素置 0 的概率。默认值：0.5
# in-place - 若设置为 True，会在原地执行操作。默认值：False
m = nn.Dropout(p=0.2)
input = autograd.Variable(torch.randn(5, 6))
output = m(input)
print(input)
print(output)

# ================================================================= #
# class torch.nn.Dropout2d(p=0.5, inplace=False)
# 随机将输入张量中整个通道设置为 0。对于每次前向调用，被置 0 的通道都是随机的。
# 通常输入来自 Conv2d 模块。
# 像在论文 Efficient Object Localization Using Convolutional Networks，如果特征图中相邻像素是强相关
# 的（在前几层卷积层很常见），那么 iid dropout 不会归一化激活，而只会降低学习率。
# 在这种情形，nn.Dropout2d()可以提高特征图之间的独立程度，所以应该使用它。
m = nn.Dropout2d(p=0.2)
input = autograd.Variable(torch.randn(2, 2, 5, 6))
output = m(input)
print(input)
print(output)

# ================================================================= #
# class torch.nn.Dropout3d(p=0.5, inplace=False)
# 随机将输入张量中整个通道设置为 0。对于每次前向调用，被置 0 的通道都是随机的。
# 通常输入来自 Conv3d 模块。

（2）BN层（BatchNormal）

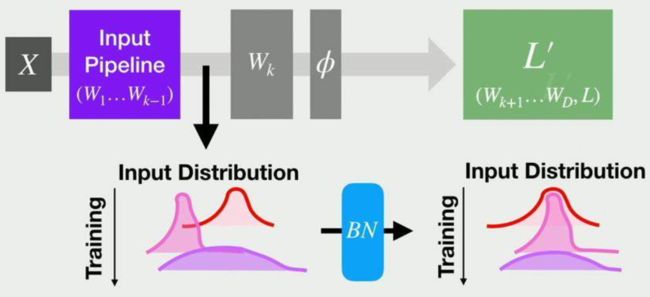
为了追求更高的性能，卷积网络被设计得越来越深，然而网络却变得难以训练收敛与调参。原因在于，浅层参数的微弱变化经过多层线性变换与激活函数后会被放大，改变了每一层的输入分布，造成深层的网络需要不断调整以适应这些分布变化，最终导致模型难以训练收敛。

由于网络中参数变化导致的内部节点数据分布发生变化的现象被称做ICS（Internal Covariate Shift）。ICS现象容易使训练过程陷入饱和区，减慢网络的收敛。前面提到的ReLU从激活函数的角度出发，在一 定程度上解决了梯度饱和的现象，而2015年提出的BN层，则从改变数据分布的角度避免了参数陷入饱和区。由于BN层优越的性能，其已经是当前卷积网络中的“标配”。

BN层首先对每一个batch的输入特征进行白化操作，即去均值方差过程。假设一个batch的输入数据为x：B=｛x1 ,…,xm｝，首先求该 batch 数据的均值与方差，如式（3-5）和式（3-6）所示。

以上公式中，m代表batch的大小，μ为批处理数据的均值，σ为批处理数据的方差。在求得均值方差后，利用式（3-7）进行去均值方差操作： 

白化操作可以使输入的特征分布具有相同的均值与方差，固定了每 一层的输入分布，从而加速网络的收敛。然而，白化操作虽然从一定程度上避免了梯度饱和，但也限制了网络中数据的表达能力，浅层学到的参数信息会被白化操作屏蔽掉，因此，BN层在白化操作后又增加了一 个线性变换操作，让数据尽可能地恢复本身的表达能力，如公式（3- 7）和公式（3-8）所示。

公式（3-8）中，γ与β为新引进的可学习参数，最终的输出为 。

BN层可以看做是增加了线性变换的白化操作，在实际工程中被证明了能够缓解神经网络难以训练的问题。

BN层的优点主要有以下3点：

• 缓解梯度消失，加速网络收敛。BN层可以让激活函数的输入数据 落在非饱和区，缓解了梯度消失问题。此外，由于每一层数据的均值与 方差都在一定范围内，深层网络不必去不断适应浅层网络输入的变化， 实现了层间解耦，允许每一层独立学习，也加快了网络的收敛。
• 简化调参，网络更稳定。在调参时，学习率调得过大容易出现震 荡与不收敛，BN层则抑制了参数微小变化随网络加深而被放大的问题，因此对于参数变化的适应能力更强，更容易调参。
• 防止过拟合。BN层将每一个batch的均值与方差引入到网络中，由于每个batch的这两个值都不相同，可看做为训练过程增加了随机噪音， 可以起到一定的正则效果，防止过拟合。 

在测试时，由于是对单个样本进行测试，没有batch的均值与方差，通常做法是在训练时将每一个batch的均值与方差都保留下来，在测试时使用所有训练样本均值与方差的平均值。

尽管BN层取得了巨大的成功，但仍有一定的弊端，主要体现在以下两点：

• 由于是在batch的维度进行归一化，BN层要求较大的batch才能有效地工作，而物体检测等任务由于占用内存较高，限制了batch的大小，这会限制BN层有效地发挥归一化功能。
• 数据的batch大小在训练与测试时往往不一样。在训练时一般采用滑动来计算平均值与方差，在测试时直接拿训练集的平均值与方差来使用。这种方式会导致测试集依赖于训练集，然而有时训练集与测试集的数据分布并不一致。

因此，我们能不能避开batch来进行归一化呢？

答案是可以的，最新的工作GN（Group Normalization）从通道方向计算均值与方差，使用更为灵活有效，避开了batch大小对归一化的影响。

具体来讲，GN先将特征图的通道分为很多个组，对每一个组内的参数做归一化，而不是batch。GN之所以能够工作的原因，笔者认为是 在特征图中，不同的通道代表了不同的意义，例如形状、边缘和纹理等，这些不同的通道并不是完全独立地分布，而是可以放到一起进行归 一化分析。

---

torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True)

• # # 参数：
• num_features： 来自期望输入的特征数，该期望输入的大小为'batch_size x num_features [x width]'
• eps： 为保证数值稳定性（分母不能趋近或取 0）,给分母加上的值。默认为 1e-5。
• momentum： 动态均值和动态方差所使用的动量。默认为 0.1。
• affine： 一个布尔值，当设为 true，给该层添加可学习的仿射变换参数。

---

BN层代码：

import torch
import torch.nn as nn
from torch import autograd

# torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True)
# 对小批量(mini-batch)的 2d 或 3d 输入进行批标准化(Batch Normalization)操作
# 在每一个小批量（mini-batch）数据中，计算输入各个维度的均值和标准差。
# gamma 与 beta 是可学习的大小为 C 的参数向量（C 为输入大小）
# 在训练时，该层计算每次输入的均值与方差，并进行移动平均。移动平均默认的动量值为 0.1。
# 在验证时，训练求得的均值/方差将用于标准化验证数据。

# # With Learnable Parameters
m = nn.BatchNorm1d(5)
# # Without Learnable Parameters
m1 = nn.BatchNorm1d(5, affine=False)
input = autograd.Variable(torch.randn(2, 5))
output = m(input)
output1 = m1(input)
print(input)
print(output)
print(output1)

# torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)
# 对小批量(mini-batch)3d 数据组成的 4d 输入进行批标准化(Batch Normalization)操作
# y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta
# With Learnable Parameters
m = nn.BatchNorm2d(1)
# Without Learnable Parameters
m1 = nn.BatchNorm2d(1, affine=False)
input = torch.Tensor([
    [[[0.1, 0.5, 1.4, 0.6, 0.8]]],
    [[[1, 0.1, 1.0, 2.0, 3.1]]]
])  # 四维张量
output = m(input)
output1 = m1(input)
print(input)
print(output)
print(output1)

# class torch.nn.BatchNorm3d(num_features, eps=1e-05, momentum=0.1, affine=True)
# 对小批量(mini-batch)4d 数据组成的 5d 输入进行批标准化(Batch Normalization)操作

（3）全连接层

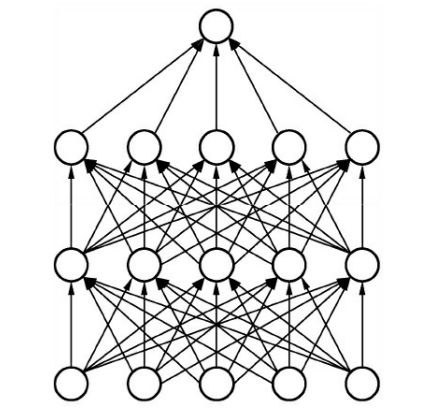
全连接层（Fully Connected Layers）一般连接到卷积网络输出的特征图后边，特点是每一个节点都与上下层的所有节点相连，输入与输出都被延展成一维向量，因此从参数量来看全连接层的参数量是最多的， 如图3 所示。

图3 全连接网络的计算过程

在物体检测算法中，卷积网络的主要作用是从局部到整体地提取图像的特征，而全连接层则用来将卷积抽象出的特征图进一步映射到特定维度的标签空间，以求取损失或者输出预测结果。

然而，随着深度学习算法的发展，全连接层的缺点也逐渐暴露了出来，最致命的问题在于其参数量的庞大。在此以VGGNet为例说明，其 第一个全连接层的输入特征为7×7×512=25088个节点，输出特征是大小为4096的一维向量，由于输出层的每一个点都来自于上一层所有点的权重相加，因此这一层的参数量为25088×4096≈。相比之下，VGGNet 最后一个卷积层的卷积核大小为3×3×512×512≈2.4×，全连接层的参数量是这一个卷积层的40多倍。

大量的参数会导致网络模型应用部署困难，并且其中存在着大量的参数冗余，也容易发生过拟合的现象。在很多场景中，我们可以使用全局平均池化层（Global Average Pooling，GAP）来取代全连接层，这种思想最早见于NIN（Network in Network）网络中，总体上，使用GAP有 如下3点好处：

• 利用池化实现了降维，极大地减少了网络的参数量。
• 将特征提取与分类合二为一，一定程度上可以防止过拟合。
• 由于去除了全连接层，可以实现任意图像尺度的输入。

全连接层代码：

import torch
import torch.nn as nn
from torch import autograd

# ================================================================= #
# # Linear Layer
# # 对输入数据做线性变换：y=Ax+b
# class torch.nn.Linear(in_features, out_features, bias=True)
# in_features - 每个输入样本的大小
# out_features - 每个输出样本的大小
# bias - 若设置为 False，这层不会学习偏置。默认值：True
m = torch.nn.Linear(20, 30)  # 随机生成 weights and bias
print(m)
input = autograd.Variable(torch.randn(128, 20))
print(input)
output = m(input)
print(output.size())
print(output)

>>>本文参考：Pytoch官方文件 &&《深度学习之PyTorch物体检测实战》

>>>如有疑问，欢迎评论区一起探讨