使用Pytorch从零开始构建WGAN

引言

在考虑生成对抗网络的文献时，Wasserstein GAN 因其与传统 GAN 相比的训练稳定性而成为关键概念之一。在本文中，我将介绍基于梯度惩罚的 WGAN 的概念。文章的结构安排如下：

1. WGAN 背后的直觉；
2. GAN 和 WGAN 的比较；
3. 基于梯度惩罚的WGAN的数学背景；
4. 使用 PyTorch 从头开始​​在；
5. CelebA-Face 数据集上实现；
6. WGAN 结果讨论。

WGAN 背后的直觉

GAN 最初由Ian J. Goodfellow 等人发明。在 GAN 中，有一个由生成器和判别器进行的双玩家最小最大游戏。早期 GAN 的主要问题是模式崩溃和梯度消失问题。为了克服这些问题，长期以来发明了许多技术。WGAN 是试图克服传统 GAN 的这些问题的方法之一。

GAN 与 WGAN

与传统的 GAN 相比，WGAN 有一些改进/变化。

1. 评论家而非判别器；
2. W-Loss 代替 BCE Loss；
3. 使用梯度惩罚/权重剪裁进行权重正则化。

传统GAN的判别器被“Critic”取代。从实现的角度来看，这只不过是最后一层没有 Sigmoid 激活的判别器。

我们稍后将讨论 WGAN 损失函数和权重正则化。

数学背景

损失函数

这是基于梯度惩罚的 WGAN 的完整损失函数。

等式 1. 具有梯度惩罚的完整 WGAN 损失函数 — [3]

看起来很吓人吧？让我们分解一下这个方程。

第 1 部分：原始批评损失

该方程产生的值应由生成器正向最大化，同时由批评家负向最大化。请注意，这里的 x_CURL 是生成器 (G(z)) 生成的图像。

这里，D 在最后一层没有 Sigmoid 激活，因此 D(*) 可以是任何实数。这给出了地球移动器的真实分布和生成分布之间的距离的近似值 - [1]。我们在这里想做的是，

1. 评论家的观点：通过最大化等式 2结果的负值/最小化正值，尽可能地将评论家对真实图像和生成图像的输出分布分开。这反映了评论家的目标，即为真实图像提供更高的分数，为更低的分数到生成的图像。
2. 生成器的观点：尝试通过以相反的方向分离真实图像和生成图像的输出分布来抵消评论家的努力。这最终使式 2 的结果的正值最大化。这反映了生成器的目标是通过欺骗 Critic 来提高生成图像的 Critic 分数。

• 在这里你可能已经注意到，Critic over Discriminator这个名字的出现是因为 Critic 不区分真假图像，只是给出一个无界的分数。

为了确保方程有效，我们需要确保 Critic 函数是 1-Lipschitz 连续的 — [1]。

1-Lipschitz连续性

函数 f(x) 是 1-L 连续的，梯度应始终小于或等于 1。

为了确保这种1-Lipschitz连续性，文献中主要提出了2种方法。

1. Weight Clipping——这是 WGAN 论文 [2] 附带的初始方法；
2. 梯度惩罚方法——这是在最初的论文之后作为改进提出的[3]。

在本文中，我们将重点关注基于梯度惩罚的 WGAN。

第二部分：梯度惩罚

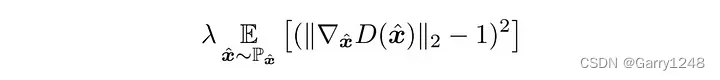
这是 Gulrajani 等人提出的梯度惩罚。——[3]。这里我们通过减小 Critic 梯度的 L2 范数与 1 之间的平方距离来强制 Critic 的梯度为 1。注意，我们不能强制 Critic 的梯度为 0，因为这会导致梯度消失问题。

等等！x(^)是什么？

考虑到 1-Lipschitz 连续性的定义，所有 x 的梯度应≤1。但实际上，确保所有可能的图像都满足这种条件是很困难的。因此，我们使用 x(^) 表示使用真实图像和生成图像作为梯度惩罚的数据点的随机插值图像。这确保了 Critic 的梯度将通过查看训练期间遇到的一组公平的数据点/图像进行正则化。

Pytorch实现

在这里，我将介绍大家应该做的必要更改，以便将传统的 GAN 更改为 WGAN。

对于下面的实现，我将使用我在之前有关 DCGAN 的文章中详细解释的模型和训练原理。

数据集

Celeba-face 数据集用于训练。下载、预处理、制作数据加载器脚本如代码1所示。

import zipfile
import os
if not os.path.isfile('celeba.zip'):
  !mkdir data_faces && wget https://s3-us-west-1.amazonaws.com/udacity-dlnfd/datasets/celeba.zip 
  with zipfile.ZipFile("celeba.zip","r") as zip_ref:
    zip_ref.extractall("data_faces/")
    
from torch.utils.data import DataLoader

transform = transforms.Compose([
                               transforms.Resize((img_size,img_size)),
                               transforms.ToTensor(),
                                transforms.Normalize((0.5,0.5, 0.5),(0.5, 0.5, 0.5))])

dataset = datasets.ImageFolder('data_faces', transform=transform)
data_loader = DataLoader(dataset,batch_size=batch_size,shuffle=True)

生成器和评论家

Critic 与 Discriminator 相同，但不包含最后一层 Sigmoid 激活。

class Generator(nn.Module):
  def __init__(self,noise_channels,img_channels,hidden_G):
    super(Generator,self).__init__()
    self.G=nn.Sequential(
        conv_trans_block(noise_channels,hidden_G*16,kernal_size=4,stride=1,padding=0),
        conv_trans_block(hidden_G*16,hidden_G*8),
        conv_trans_block(hidden_G*8,hidden_G*4),
        conv_trans_block(hidden_G*4,hidden_G*2),
        nn.ConvTranspose2d(hidden_G*2,img_channels,kernel_size=4,stride=2,padding=1),
        nn.Tanh()
    )
  def forward(self,x):
    return self.G(x)

class Critic(nn.Module):
  def __init__(self,img_channels,hidden_D):
    super(Critic,self).__init__()
    self.D=nn.Sequential(
        conv_block(img_channels,hidden_G),
        conv_block(hidden_G,hidden_G*2),
        conv_block(hidden_G*2,hidden_G*4),
        conv_block(hidden_G*4,hidden_G*8),
        nn.Conv2d(hidden_G*8,1,kernel_size=4,stride=2,padding=0))
    
  def forward(self,x):
    return self.D(x)

Generator 和 Critic 的支持块如下面的代码 3 所示。

class conv_trans_block(nn.Module):
  def __init__(self,in_channels,out_channels,kernal_size=4,stride=2,padding=1):
    super(conv_trans_block,self).__init__()
    self.block=nn.Sequential(
        nn.ConvTranspose2d(in_channels,out_channels,kernal_size,stride,padding),
        nn.BatchNorm2d(out_channels),
        nn.ReLU())
  def forward(self,x):
    return self.block(x)

class conv_block(nn.Module):
  def __init__(self,in_channels,out_channels,kernal_size=4,stride=2,padding=1):
    super(conv_block,self).__init__()
    self.block=nn.Sequential(
        nn.Conv2d(in_channels,out_channels,kernal_size,stride,padding),
        nn.BatchNorm2d(out_channels),
        nn.LeakyReLU(0.2))
  def forward(self,x):
    return self.block(x)

损失函数

与任何其他典型的损失函数不同，损失函数可能有点棘手，因为它包含梯度。在这里，我们将使用梯度惩罚来实现 W-loss，稍后可以将其插入 WGAN 模型中。

def get_gen_loss(crit_fake_pred):
  gen_loss= -torch.mean(crit_fake_pred)
  return gen_loss

def get_crit_loss(crit_fake_pred, crit_real_pred, gradient_penalty, c_lambda):
  crit_loss= torch.mean(crit_fake_pred)- torch.mean(crit_real_pred)+ c_lambda* gradient_penalty
  return crit_loss

让我们分解一下代码 4 中所示的损失函数。

1. 生成器损失 - 生成器损失不受梯度惩罚的影响。因此，它必须仅最大化 D(x_CURL)/ D(G(z)) 项，这意味着最小化 -D(G(z))。这是在第 2 行中实现的。
2. 批评者损失 - 批评者损失包含等式 1 中所示损失的 2 个部分。在第 6 行中，前两项给出等式 2 中解释的原始批评者损失，而最后一项给出等式 3 中解释的梯度惩罚。

梯度惩罚可以按照下面的代码 5 来实现 - [1]。

def get_gradient(crit, real_imgs, fake_imgs, epsilon):

  mixed_imgs= real_imgs* epsilon + fake_imgs*(1- epsilon)
  mixed_scores= crit(mixed_imgs)

  gradient= torch.autograd.grad(outputs= mixed_scores,
                                inputs= mixed_imgs,
                                grad_outputs= torch.ones_like(mixed_scores),
                                create_graph=True,
                                retain_graph=True)[0]
  return gradient

def gradient_penalty(gradient):
  gradient= gradient.view(len(gradient), -1)
  gradient_norm= gradient.norm(2, dim=1)
  penalty = torch.nn.MSELoss()(gradient_norm, torch.ones_like(gradient_norm))
  return penalty

在代码 5 中，get_gradient()函数返回从x_hat （混合图像）开始到Critic 输出 (mixed_scores)结束的所有网络梯度。这将在gradient_penalty()函数中使用，它返回Critic梯度的1和L2范数之间的均方距离。

减少 Critic 的损失最终会减少这种梯度惩罚。这确保了 Critic 函数保留了 1-Lipschitz 连续性。

训练

训练将与上一篇文章中的几乎相同。但这里的损失与传统的 GAN 损失不同。我已经使用WANDB记录我的结果。如果您有兴趣记录结果，WANDB 是一个非常好的工具。

C=Critic(img_channels,hidden_C).to(device)
G=Generator(noise_channels,img_channels,hidden_G).to(device)

#C=C.apply(init_weights)
#G=G.apply(init_weights)

wandb.watch(G, log='all', log_freq=10)
wandb.watch(C, log='all', log_freq=10)

opt_C=torch.optim.Adam(C.parameters(),lr=lr, betas=(0.5,0.999))
opt_G=torch.optim.Adam(G.parameters(),lr=lr, betas=(0.5,0.999))

gen_repeats=1
crit_repeats=3

noise_for_generate=torch.randn(batch_size,noise_channels,1,1).to(device)

losses_C=[]
losses_G=[]

for epoch in range(1,epochs+1):
  loss_C_epoch=[]
  loss_G_epoch=[]

  for idx,(x,_) in enumerate(data_loader):
    C.train()
    G.train()

    x=x.to(device)
    x_len=x.shape[0]

    ### Train C

    loss_C_iter=0
    for _ in range(crit_repeats):
      opt_C.zero_grad()
      z=torch.randn(x_len,noise_channels,1,1).to(device)

      real_imgs=x
      fake_imgs=G(z).detach()

      real_C_out=C(real_imgs)
      fake_C_out=C(fake_imgs)

      epsilon= torch.rand(len(x),1,1,1, device= device, requires_grad=True)
      gradient= get_gradient(C, real_imgs, fake_imgs.detach(), epsilon)
      gp= gradient_penalty(gradient)
      loss_C= get_crit_loss(fake_C_out, real_C_out, gp, c_lambda=10)

      loss_C.backward()
      opt_C.step()

      loss_C_iter+=loss_C.item()/crit_repeats

    ### Train G
    loss_G_iter=0
    for _ in range(gen_repeats):
      opt_G.zero_grad()
      z=torch.randn(x_len,noise_channels,1,1).to(device)
      fake_C_out = C(G(z))
      loss_G= get_gen_loss(fake_C_out)
      loss_G.backward()
      opt_G.step()

      loss_G_iter+=loss_G.item()/gen_repeats

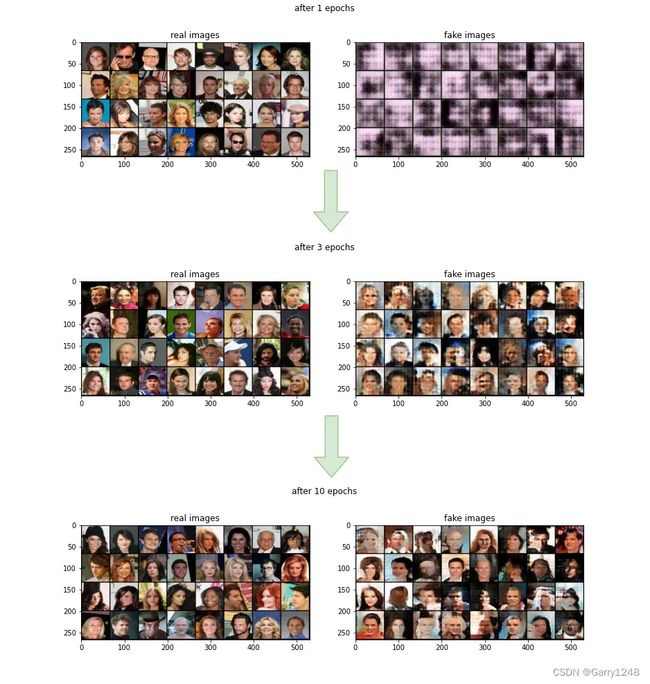
结果

这是经过 10 个 epoch 训练后获得的结果。与传统 GAN 一样，生成的图像随着时间的推移变得更加真实。WANDB 项目的所有结果都可以在这里找到。

结论

生成对抗网络一直是深度学习社区的热门话题。由于 GAN 传统训练方法的缺点，WGAN 随着时间的推移变得越来越流行。这主要是因为它对模式崩溃具有鲁棒性并且不存在梯度消失问题。在本文中，我们实现了一个能够生成人脸的简单 WGAN 模型。

请随意查看 GitHub 代码。如有任何意见、建议和意见，我们将不胜感激。

Reference

[1] GAN specialization on coursera

[2] Arjovsky, Martin et al. “Wasserstein GAN”

[3] Gulrajani, Ishaan et al. “Improved Training of Wasserstein GANs”

[4] Goodfellow, Ian et al. “Generative Adversarial Networks”

[5] Vincent Herrmann, “Wasserstein GAN and the Kantorovich-Rubinstein Duality”

[6] Karras, Tero et al. “A Style-Based Generator Architecture for Generative Adversarial Networks”

本文译自Udith Haputhanthri的博文。