算法中的数学知识总结

数学知识补充

算术基本定理：
任何一个大于1的正整数都能唯一分解为有限个质数的乘积，可写作：
$$N=p_1^{c_1}{p}_2^{c_2}\dots p_k^{c_k}$$
其中，c都是正整数，$p_i$都是质数，且满足$p_1<p_2<\cdots <p_k$
费马小定理： 若 p 是质数，则对于任意整数 a ，有 $a^p\equiv a(modp)$。
欧拉定理： 若正整数 a ，n 互质，则 $a^{\varphi (n)}\equiv 1(modn)$，其中，$\varphi (n)$ 为欧拉函数。
裴蜀定理： 若 a，b 是整数,且 gcd(a,b)=d，那么对于任意的整数 x，y，ax+by 都一定是 d 的倍数，特别地，一定存在整数 x，y，使 ax+by = d 成立。

一、质数

定义： 在大于 1 的自然数中，除了 1 和它本身以外不再有其他因数的自然数。

Ⅰ试除法判定质数

1、朴素做法$O(n)$:

①如果 n 小于 2 ，则 n 不是质数。
②枚举从 2 到 n - 1 的所有数，判断是否能被 n 整除。

bool is_prim(int n)
{
    if(n < 2) return false;
    for(int i = 2;i < n;i++)
    {
        if(n % i == 0) return false;
    }
    return true;
}

2、优化$O(\sqrt{n})$:

设 d 为待判定数 n 的一个因子，那么 $\frac{n}{d}$ 也必定是 n 的一个因子。
例如：$\mathrm{d}=3,\frac{\mathrm{n}}{\mathrm{d}}=4$，3 可以整除 12，4 也可以整除 12。

一个性质：成对的两个因子中，必只有一个小于等于$\sqrt{n}$
证明如下：
若两个因子都大于 $\sqrt{n}$，即 $d>\sqrt{n},\frac{n}{d}>\sqrt{n}$，则
$d\ast \frac{n}{d}=n>\sqrt{n}\ast \sqrt{n}=n$
得到 $n>n$，矛盾，所以两个因子必然只有一个小于等于$\sqrt{n}$

因此在代码中，在 2~(n - 1) 中只要有一个为 n 的因子就能判定 n 是合数而不是质数，所以只需要从 2 枚举到 $\sqrt{n}$ 即可（$i\le \sqrt{n}$）。
关于该处的写法：
①$\mathrm{i}<=\mathrm{sqrt}(\mathrm{n})$ : 因为 sqrt() 函数运行比较满，不推荐。
②$\mathrm{i}\ast \mathrm{i}<=\mathrm{n}$：int 的最大值为 2147483647（$2^{31}-1$)，i * i可能发生溢出，不推荐。
所以采用 $\mathrm{i}<=n/i$该写法。

bool is_prim(int n)
{
    if(n < 2) return false;
    for(int i = 2;i <= n / i;i++)
    {
        if(n % i == 0) return false;
    }
    return true;
}

Ⅱ分解质因数

枚举 2 到 $\sqrt{n}$ 的数判断是否是 n 的因子。

为什么枚举所有数，不是要质因数吗？
①当枚举到 i 时，2 到 i - 1 的所有 n 的质因子都会除 n 。
所以当枚举到 i 时，2 到 i - 1 中没有 n 的质因子。
②且当 n % i == 0条件成立时，说明 n 是 i 的倍数，此时 2 到 i - 1 中也没有 i 的质因子，根据质数的定义，i 必定是质数。

void divide(int a)
{
    for(int i = 2;i <= a / i;i++)
    {
        if(a % i == 0)
        {
            int s = 0;
            while(a % i == 0)
            {
                s++;
                a /= i;
            }
            cout<<i<<" "<<s<<endl;
        }
    }
    //最后如果n还是>1，说明这就是大于sqrt(n)的唯一质因子，输出即可。
    cout<<endl;
}

Ⅲ筛质数

1、朴素筛法$O(nlogn)$(将所有数的倍数筛掉):

void get_prime(int n)
{
    for(int i = 2;i <= n;i++)
    {
        if(!st[i]) //如果为质数
        {
            prime[cnt++] = i;
        }
        //将每一个数的倍数筛掉
        for(int j = i + i;j <= n;j += i)
        {
            st[j] = true;
        }
    }
}

2、埃氏筛$O(loglogn)$(将质数的倍数筛掉):

void get_prime(int n)
{
    for(int i = 2;i <= n;i++)
    {
        if(st[i]) continue;//st判断是否被筛掉
        prime[cnt++] = i;
        for(int j = i + i;j <= n;j += i)
        {
            st[j] = true;
        }
    }
}

3、线性筛，也叫欧拉筛$O(n)$(合数会被自己的最小质因子筛掉):

$p_j$:表示下标为 j 的质数

①当 i % $p_j$ == 0:
pj是i的质因子，pj也是pj*i的质因子，同时是最小质因子
②当 i % $p_j$ != 0:
由于 $p_j$ 是从小到大枚举的质数且 i % $p_j$ ==0的话说明 $p_j$是 i 的最小质因子，可现在不是，说明 $p_j$ 一定小于 i 的最小质因子，$p_j$ 是 $p_j\ast i$ 的最小质因子
总结：无论哪种情况，$p_j$ 都是 $p_j\ast i$ 的最小质因子，即：$p_j\ast i$ (合数)一定会被它的最小质因子筛掉。

void get_prime(int n)
{
    for(int i = 2;i <= n;i++)
    {
        if(!st[i])
        {
            prime[cnt++] = i;
        }
        for(int j = 0;prime[j] <= n / i;j++)//枚举所有质数
        {
            st[prime[j] * i] = true;//筛掉该质数对应的合数
            if(i % prime[j] == 0) break;
        }
    }
}

二、约数

Ⅰ试除法求约数

从 1 枚举到 $\sqrt{n}$ ,判断 i 是否能整除 n ，对于大于 $\sqrt{n}$ 的约数，可以通过 $\frac{n}{d}$ 计算得出。

vector<int> get_divisors(int n)
{
    vector<int> res;
    for(int i = 1;i <= n / i;i++)
    {
        if(n % i == 0)
        {
            res.push_back(i);
            if(i != n / i) res.push_back(n / i);
        }
    }
    sort(res.begin(),res.end());
    return res;
}

Ⅱ约数个数

公式：$(c_1+1)(c_2+1)\dots (c_k+1)$

求 N 的约数个数：
由算术基本定理得：$N=p_1^{c_1}{p}_2^{c_2}\dots p_k^{c_k}$
设 d 为 N 的约数：$d=p_1^{{\beta }_1}{p}_2^{{\beta }_2}\dots p_k^{{\beta }_k}$
对于 ${\beta }_1$ 有 $0\le {\beta }_1\le c_1$，根据算术基本定理，${\beta }_1,c_1$ 都为正整数，则 ${\beta }_1$ 有 $(c_1+1)$ 中不同的选法，对 ${\beta }_2$~${\beta }_k$ 同上。
根据组合，则约数个数为$(c_1+1)(c_2+1)\dots (c_k+1)$

#include 
#include 

using namespace std;

const int mod = 1e9 + 7;
map<int,int> prime;

void get_divisor(int n)
{
    for(int i = 2;i <= n / i;i++)
    {
        if(n % i == 0)
        {
            while(n % i == 0)
            {
                n /= i;
                prime[i]++;
            }
        }
    }
    if(n > 1) prime[n]++;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a;
        cin>>a;

        get_divisor(a);
    }
    long long res = 1;
    for(auto p : prime)
    {
        res = res * (p.second + 1) % mod;
    }
    cout<<res<<endl;
    return 0;
}

Ⅲ约数之和

公式： $(p_1^0+p_1^1+\cdots +p_1^{c_1})\dots (p_k^0+p_k^1+\cdots +p_k^{c_k})$

#include 
#include 

using namespace std;

map<int,int> prime;
const int mod = 1e9 + 7;

void get_divisor(int n)
{
    for(int i = 2;i <= n / i;i++)
    {
        if(n % i == 0)
        {
            while(n % i == 0)
            {
                n /= i;
                prime[i]++;
            }
        }
    }
    if(n > 1) prime[n]++;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a;
        cin>>a;
        get_divisor(a);
    }
    long long res = 1;
    for(auto i : prime)
    {
        long long t = 1;
        int p = i.first,a = i.second;
		//p是质数，a是指数
		//1 * p + 1
		//p^2 + p + 1
		//p^3 + p^2 + p + 1
        while(a--) t = (t * p + 1) % mod;
        res = res * t % mod;
    }
    cout<<res<<endl;
}

Ⅳ欧几里得算法

gcd(a,b): 求 a 和 b 的最大公约数

证明 gcd(a,b) = gcd(b,a mod b):
①从左往右：
设 d = gcd(a,b)
因为对应左边 d | a，d | b，所以 d | (ax + by) (d 能整除 a 的若干倍 + b 的若干倍)
a mod b = a - $\lfloor \frac{\mathrm{a}}{\mathrm{b}}\rfloor$ * b
令 c = $\lfloor \frac{\mathrm{a}}{\mathrm{b}}\rfloor$(c 为常数)
所以 a mod b = a - c * b
所以 对应右边 d | b，d | (a - c * b)
②从右往左：
设 d = gcd(b，a mod b)
因为 d | b，d | (a - c * b)
所以 d | [(a - c * b) + c * b] = d | a，对应右边
证毕！

int gcd(int a,int b)
{
    return !b ? a : gcd(b,a % b);
}

三、欧拉函数

定义： 1 ~ N 中与 N 互质的数的个数被称为欧拉函数，记为 $\varphi (N)$，若在算术基本定理中，$N=p_1^{c_1}{p}_2^{c_2}\dots p_k^{c_k}$，则：
$$\varphi (N)=N\ast (1-\frac{1}{p_1})\ast (1-\frac{1}{p_2})\dots (1-\frac{1}{p_m})$$
规定 $\varphi (1)=1$

推导：为了求 1 - N 中和 N 互质的数的个数
①从 1 ~ N 中去掉 $p_1，p_2，\dots ，p_k$ 的所有倍数
$$N-\frac{N}{p_1}-\frac{N}{p_2}-\cdots -\frac{N}{p_k}$$
②若一个数既是 $p_1$的倍数，又是 $p_2$ 的倍数，根据①，则该数被去掉了两次，加上所有 $p_i\ast p_j$ 的倍数
$$+\frac{N}{p_1{p}_j}+\frac{N}{p_1{p}_3}+\cdots +$$
③若一个数既是 $p_1$的倍数，又是 $p_2$ 的倍数，也是 $p_3$ 的倍数，
根据①，该数被去掉了三次，根据②，该数被加上了三次，我们应该让这个数去掉一次，减去 $p_i\ast p_j\ast p_k$ 的倍数
$$-\frac{N}{p_1{p}_2{p}_3}-\frac{N}{p_1{p}_2{p}_4}-\cdots -$$
④会发现相关规律，并将欧拉函数 $\varphi (N)=N\ast (1-\frac{1}{p_1})\ast (1-\frac{1}{p_2})\dots (1-\frac{1}{p_m})$ 展开即可得到此式。

int phi(int n)
{
    int res = n;
    for(int i = 2;i <= n / i;i++)
    {
        if(n % i == 0)
        {
            res = res / i * (i - 1);
            while(n % i == 0) n /= i;
        }
    }
    if(n > 1) res = res / n * (n - 1);
    return res;
}

筛法求欧拉函数

①若一个数是质数，设此数为 p ,则根据欧拉函数与质数定义，1 ~ p 中与 p 互质的数的个数为 p - 1，即 $\varphi (p)=p-1$。
②当 i % $p_j$ == 0 时，求 $\varphi (p_j\ast i)$:
当 i % $p_j$ == 0 时，$p_j$ 为 i 的最小质因子，$p_j$ 为 $p_j\ast i$ 的最小质因子。
根据欧拉函数定义得：
$$\varphi (i)=i\ast (1-\frac{1}{p_1})\ast (1-\frac{1}{p_2})\dots (1-\frac{1}{p_m})$$
则
$$\begin{array}{rl}\varphi (p_j\ast i)& =p_j\ast i\ast (1-\frac{1}{p_1})\ast (1-\frac{1}{p_2})\dots (1-\frac{1}{p_m})\\ & =p_j\ast \varphi (i)\end{array}$$
③当 i % $p_j\ne$ 0 时，求 $\varphi (p_j\ast i)$:
$p_j$ 不是 i 的质因子：
$$\varphi (i)=i\ast (1-\frac{1}{p_1})\ast (1-\frac{1}{p_2})\dots (1-\frac{1}{p_m})$$
其中，不包含 $1-\frac{1}{p_j}$。
但是 $p_j$ 是 $i\ast p_j$ 的质因子：
$$\begin{array}{rl}\varphi (p_j\ast i)& =p_j\ast i\ast (1-\frac{1}{p_1})\ast (1-\frac{1}{p_2})\dots (1-\frac{1}{p_m})\ast (1-\frac{1}{p_j})\\ & =p_j\ast \varphi (i)\ast (1-\frac{1}{p_j})\\ & =\varphi (i)\ast (p_j-1)\end{array}$$

void get_eular()
{
    eular[1] = 1; 
    for(int i = 2;i <= n;i++)
    {
        if(!st[i])
        {
            primes[cnt ++] = i;
            eular[i] = i - 1;
        }
        for(int j = 0;primes[j] <= n / i;j++)
        {
            int t = primes[j] * i;
            st[primes[j] * i] = true;
            if(i % primes[j] == 0)
            {
                eular[t] = eular[i] * primes[j];
                break;
            }
            eular[t] = eular[i] * (primes[j] - 1);
        }
    }
}

四、快速幂

为了在 $O(logk)$ 的时间复杂度中，求 $a^{k}modp$。

将 a 分解，将 k 用二进制表示：
$$k=2^{x_1}+2^{x_2}+\cdots +2^{x_t}$$
则
$$\begin{array}{rl}{a}^k& =a^{2^{x_1}+2^{x_2}+\cdots +2^{x_t}}\\ & =a^{2^{x_1}}\ast a^{2^{x_2}}\ast \cdots \ast a^{2^{x_t}}\end{array}$$
对于每个因子如何递推得到：
$$\begin{array}{rl}& a^{2^0}\ast a^{2^0}=a^{2^1}\\ & a^{2^1}\ast a^{2^1}=a^{2^2}\\ & ⋮\\ & a^{2^{logk-1}}\ast a^{2^{logk-1}}=a^{2^{logk}}\end{array}$$

LL qmi(LL a,LL b,LL p)
{
    LL res = 1 % p;
    while(b)
    {
        if(b & 1) res = res * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return res;
}

快速幂求逆元

乘法逆元：$\frac{a}{b}\equiv a\ast x(modp)$
可以理解为：$b\ast x\equiv 1(modp)$，若 b 为 p 的倍数，则 $b\ast x\equiv 0(modp)$ ，即不存在逆元。
由费马小定理得：
$$\begin{array}{rl}{b}^{p-1}& \equiv 1(modp)\\ b\ast b^{p-2}& \equiv 1(modp)\end{array}$$
则 $b^{p-2}$ 即 $b(modp)$ 的乘法逆元。

#include 

using namespace std;
typedef long long LL;

LL qmi(int a,int k,int p)
{
    LL res = 1,t = a;
    while(k)
    {
        if(k & 1) res = res * t % p;
        t = t * t % p;
        k >>= 1;
    }
    return res;
}

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,p;
        cin>>a>>p;
        if(a % p == 0) cout<<"impossible"<<endl;
        else cout<<qmi(a,p - 2,p)<<endl;
    }
    return 0;
}

五、扩展欧几里得算法

利用裴蜀定理求 x，y：
①当 b = 0 时：gcd(a,0) = a。
$$ax+by=ax+0\ast y=a$$
显然，x = 1,y = 0 是其中的一组解。
②当 b $\ne$ 0 时：令 d = gcd(b,a mod b)。
为了方便计算，将 x，y对调，即 d = exgcd(b,a mod b,y,x)
$$\begin{array}{rl}d& =by+(amodb)x\\ & =by+(a-\lfloor \frac{a}{b}\rfloor b)x\\ & =ax+b(y-\lfloor \frac{a}{b}\rfloor x)\end{array}$$
将 a，b的系数对应，发现 x 不变，y 发生了改变。

int gcd(int a,int b,int &x,int &y)
{
    if(!b)
    {
        x = 1,y = 0;
        return a;
    }
    int d = gcd(b,a % b,y,x);
    y -= (a / b) * x;
    return d;
}

六、高斯消元解线性方程组

枚举每一列 c
①找到当前列的绝对值最大的一行。
②将该行换到最上面。
③将该行的第一个数变成 1（该行的所有数除以该行第一个数，从后往前求）。
④将当前列 c 该行下面所有行消成 0。
⑤将主元上面的数消成 0。

#include 
#include 

using namespace std;
const int N = 110;
const double eps = 1e-6;
int n;
double a[N][N];

int gauss()
{
    int c,r;
    for(c = 0,r = 0;c < n;c++)//枚举每一列
    {
        int t = r;//用t记录从当前行往下，找到当前列绝对值最大的一行
        for(int i = r;i < n;i++)
        {
            if(fabs(a[i][c]) > fabs(a[t][c])) t = i;
        }

        if(fabs(a[t][c]) < eps) continue;//若当前列的绝对值最大的为0，跳过当前列
        for(int i = c;i <= n;i++) swap(a[r][i],a[t][i]);//对绝对值最大的行的所有数交换到最上面
        for(int i = n;i >= c;i--) a[r][i] /= a[r][c];//将该行第一个数变成1，即该行的所有数都除以该行第一个数，倒着算，防止第一个数除了自己后发生改变

        for(int i = r + 1;i < n;i++)//即将当前列，该行（r）下面(r + 1)的所有数变成0
        {
            if(fabs(a[i][c]) > eps)
            {
                for(int j = n;j >= c;j--)
                {
                    a[i][j] -= a[i][c] * a[r][j];//将第r+1行开始的第一个数记为k，则(r + 1) -= k * r(将第r+1行往下的数减去第r行的k倍)
                }
            }
        }
        r++;
    }

    //判断方程解的情况
    if(r < n)//r < n说明r行以后的方程组左边为0
    {
        for(int i = r;i < n;i++)
        {
            if(fabs(a[i][n]) > eps) return 0;//若方程组右边有大于0的数，则方程组无解
        }
        return 2;//否则有无穷多组解
    }

    //前面都不满足，说明该方程组有唯一解
    for(int i = n - 2;i >= 0;i--)
    {
        for(int j = i + 1;j < n;j++)
        {
            a[i][n] -= a[i][j] * a[j][n];
        }
    }
    //将主元上面的数都消成0
    //当n = 3时
    /*        n - 3  n - 2   n - 1    n
        n - 3:  1     0.5    -1.5   -4.5
        n - 2:  0      1      1/3    -1
        n - 1:  0      0       1      3
    */
    return 1;
}
int main()
{
    cin>>n;
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j < n + 1;j++)
        {
            cin>>a[i][j];
        }
    }

    int t = gauss();
    if(t == 1)
    {
        for(int i = 0;i < n;i++)
            printf("%.2lf\n",a[i][n]);
    }
    else if(t == 0) puts("No solution");
    else puts("Infinite group solutions");
    return 0;
}

七、组合数

Ⅰ公式法（1<= b <= a <= 2000）

$C_a^b=C_{a-1}^b+C_{a-1}^{b-1}$

#include 

using namespace std;

const int N = 2010,mod = 1e9 + 7;

int c[N][N];

int n;
int main()
{
    cin>>n;
    for(int i = 0;i < N;i++)
    {
        for(int j = 0;j <= i;j++)
        {
            if(!j) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
        }
    }

    while(n--)
    {
        int a,b;
        cin>>a>>b;
        cout<<c[a][b]<<endl;
    }
    return 0;
}

Ⅱ 快速幂（1 <= b <= a <= $10^5$）

$C_a^b=\frac{a!}{(a-b)!b!}$

①预处理 i 的阶乘 fact[i] (mod 1e9 + 7)
②预处理 i 的阶乘的逆元 infact[i] (mod 1e9 + 7)
③$C_a^b=fact[a]\ast infact[a-b]\ast infact[b]$

#include 

using namespace std;

const int N = 100010;
const int mod = 1e9 + 7;
typedef long long LL;
int fact[N],infact[N];

LL qmi(LL a,LL b,LL p)
{
    LL res = 1,t = a;
    while(b)
    {
        if(b & 1) res = res * t % p;
        t = t * t % p;
        b >>= 1;
    }
    return res;
}
int main()
{
    int n;
    cin>>n;

    fact[0] = infact[0] = 1;
    for(int i = 1;i < N;i++)
    {
        fact[i] = (LL)fact[i - 1] * i % mod;
        infact[i] = (LL)infact[i - 1] * qmi(i,mod - 2,mod) % mod;
    }
    while(n--)
    {
        int a,b;
        cin>>a>>b;

        cout<<(LL)fact[a] * infact[a - b] % mod * infact[b] % mod<<endl;
    }
    return 0;
}

Ⅲ 卢卡斯定理（1 <= b <= a <= $10^{18}$）

$C_a^b=C_{amodp}^{bmodp}{C}_{a/p}^{b/p}(modp)$
$C_a^b=\frac{a!}{(a-b)!b!}=\frac{(a-b+1)\dots a}{b!}$

#include 

using namespace std;
typedef long long LL;
int p;
LL qmi(LL a,LL b,LL p)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) res = res * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return res;
}

LL c(LL a,LL b)
{
    if(a < b) return 0;   
    LL res = 1;
    for(int i = 1,j = a;i <= b;i++,j--)
    {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i,p - 2,p) % p;
    }
    return res;
}

LL lucas(LL a,LL b,int p)
{
    if(a < p && b < p) return c(a,b);
    return (LL)c(a % p,b % p) * lucas(a / p,b / p,p) % p;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        LL a,b;
        cin>>a>>b>>p;
        cout<<lucas(a,b,p)<<endl;
    }
    return 0;
}

Ⅳ 高精度

$C_a^b=\frac{a!}{(a-b)!b!}$

1~n中 p 的倍数的个数为 $\lfloor \frac{n}{p}\rfloor$，例：1~8中 2 的倍数的个数为 $\lfloor \frac{8}{2}\rfloor =4$
因为 $n!=n\ast (n-1)\dots 2\ast 1$
所以 n! 中 p 的倍数的个数等于 1~n 中 p 的倍数的个数
因此 n! 中包含 p 的个数 = $\lfloor \frac{n}{p}\rfloor +\lfloor \frac{n}{p^2}\rfloor +\lfloor \frac{n}{p^3}\rfloor +\dots$

① （线性筛）因为 a >= b，a > a - b，所以只需预处理 a 中所有的质因数（a! 中所有的质因数相当于 a 中的所有质因数）
②利用上述性质将 $C_a^b$ 分解质因数，
即：$C_a^b$ 中 p 的个数为：a! 中 p 的个数 - b! 中 p 的个数 - (a - b)! 中 p 的个数。
③根据算术基本定理得到 $C_a^b$，其中乘法使用高精度。

#include 
#include 

using namespace std;
const int N = 5010;

int prime[N],cnt;
bool st[N];
int sum[N];

void get_prime(int n)
{
    for(int i = 2;i < N;i++)
    {
        if(!st[i]) prime[cnt++] = i;
        for(int j = 0;prime[j] <= n / i;j++)
        {
            st[prime[j] * i] = true;
            if(i % prime[j] == 0) break;
        }
    }
}

int get(int n,int p)
{
    int res = 0;
    while(n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}

vector<int> mul(vector<int> a,int b)
{
    vector<int> res;
    int t = 0;
    for(int i = 0;i < a.size();i++)
    {
        t += a[i] * b;
        res.push_back(t % 10);
        t /= 10;
    }
    while(t)
    {
        res.push_back(t % 10);
        t /= 10;
    }
    return res;
}


int main()
{
    int a,b;
    cin>>a>>b;
    get_prime(a);

    for(int i = 0;i < cnt;i++)
    {
        int p = prime[i];
        sum[i] = get(a,p) - get(b,p) - get(a - b,p);
    }

    vector<int> res;
    res.push_back(1);

    for(int i = 0;i < cnt;i++)
    {
        for(int j = 0;j < sum[i];j++)
        {
            int p = prime[i];
            res = mul(res,p);
        }
    }

    for(int i = res.size() - 1;i >= 0;i--)
    {
        cout<<res[i];
    }
    return 0;
}

卡特兰数

以满足条件的01序列为例：
将该题转化为网格图，以 n = 6为例，规定：0 表示向右走，1表示向上走。

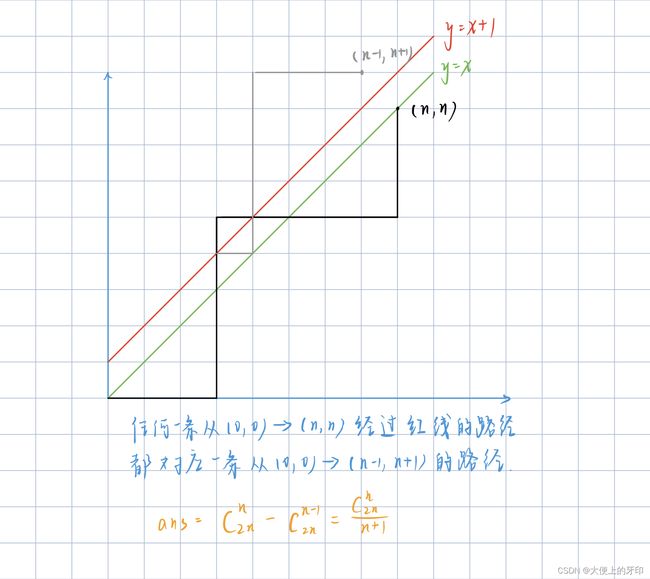
图片来源，借用一下QAQ
①将 n 个 0 和 n 个 1 组合成排列长度为 2n 的序列，对应网格图中不同的路径。
总路径个数为 $C_{12}^6$，即 12 个数中选 0 的方案数。
②对于任意前缀 0 的个数不少于 1 的个数，可转化为网格图中不经过红线的路径个数，从而转化为：
所有路径个数（$C_{12}^6$) - 经过红线的路径个数
③对于任意一条经过红线的路径，其终点是固定的（6，6），以经过红线点为起始点，将其关于红线对称后，其终点依然固定（5，7），则经过红线的路径个数可转化为从（0，0）到（5，7）的个数（$C_{12}^5$）
答案为：$C_{2n}^n-C_{2n}^{n-1}(C_{12}^6-C_{12}^5)$
化简：
$$\begin{array}{rl}& C_{2n}^n-C_{2n}^{n-1}\\ =& \frac{(2n)!}{n!n!}-\frac{(2n)!}{(n+1)!(n-1)!}\\ =& \frac{(2n)!(n+1)-(2n)!n}{(n+1)!n!}\\ =& \frac{(2n)!}{(n+1)!n!}\\ =& \frac{1}{n+1}\frac{(2n)!}{n!n!}\\ =& \frac{1}{n+1}{C}_{2n}^n(卡特兰数)\end{array}$$

#include 

using namespace std;
typedef long long LL;

const int mod = 1e9 + 7;
LL qmi(int a,int b,int p)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) res =(LL)res * a % mod;
        a = (LL)a * a % mod;
        b >>= 1;
    }
    return res;
}

int c(int a,int b)
{
    LL res = 1;
    for(int i = 1,j = a;i <= b;i++,j--)
    {
        res = (LL)res * j % mod;
        res = (LL)res * qmi(i,mod - 2,mod) % mod;
    }
    return res;
}
int main()
{
    int n;
    cin>>n;
    cout<<(LL)c(2 * n,n) * qmi(n + 1,mod - 2,mod) % mod<<endl;
    return 0;
}