算法-回溯法
回溯法就是一种有组织的系统化搜索技术,可以看作是蛮力法穷举搜索的改进。
回溯法每次只构造可能解的一部分,然后评估这个部分解,如果这个部分解有可能导致一个完整解,则对其进一步构造,否则,就不必继续构造这个部分解了。回溯法常常可以避免搜索所有的可能解,所以,它适用于求解组合数量较大的问题。
概述
问题的解空间
复杂问题常常有很多的可能解,这些可能解构成了问题的解空间。解空间也就是进行穷举的搜索空间,所以,解空间中应该包括所有的可能解。
为了用回溯法求解一个具有n个输入的问题,一般情况下,将其可能解表示为满足某个约束条件的等长向量X=(x1,x2,……,xn),其中分量xi(1<=i<=n)的取值范围是某个有限几何Si={ai1,ai2,……,airi},所有可能的解向量构成了问题的解空间。
问题的解空间一般用解空间树的方式组织,因为解空间树能将解空间形象化。如0/1背包问题,
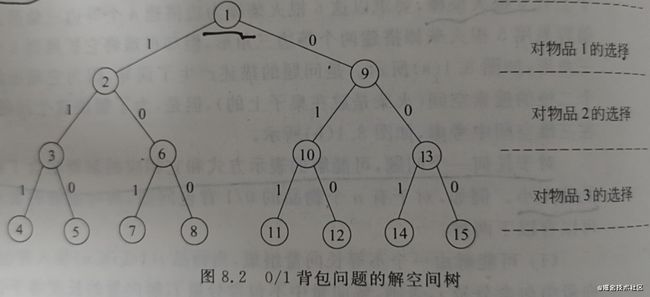
解空间的动态搜索
蛮力法是对整个解空间树中的所有可能解进行穷举搜索的一种方法,但是,只有满足约束条件的解才是可行解,只有满足目标函数的解才是最优解,这就有可能减少搜索空间。回溯法从根节点出发,按照深度优先策略遍历解空间树,搜索满足约束条件的解。在搜索至树中任一结点时,先判断该结点对应的部分解是否满足约束条件,或者是否超出目标函数的界,也就是判断该节点是否包含问题的(最优)解,如果肯定不包含,则跳过对以该结点为根的子树的搜索,即所谓的剪枝;否则,进入以该结点为根的子树,继续按照深度优先策略搜索。
回溯法的搜索过程涉及的结点只是整个解空间树的一部分,在搜索过程中,通常采用两种策略避免无效搜索:(1)用约束条件减去得不到可行解的子树;(2)用目标函数剪去得不到最优解的子树。这两类函数统称为剪枝函数。
回溯法的求解过程
图问题中的回溯法
图着色问题
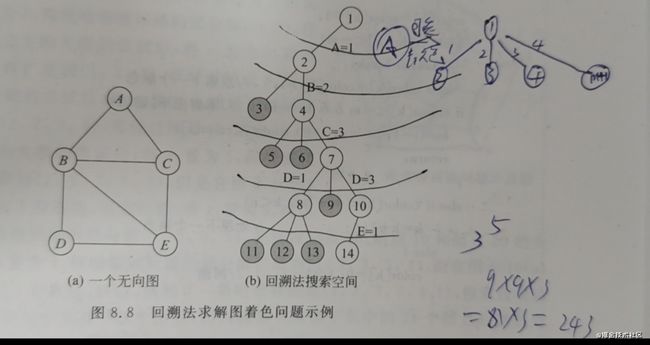
图着色问题描述为:给定无向连通图G=(V,E)和正整数m,求最小的整数m,使得用m种颜色对G中的顶点着色,使得任意两个相邻顶点着色不同。
首先把所有顶点的颜色初始化为0,然后依次为每个顶点着色。在图着色问题的解空间树中,如果从根节点到当前节点对应一个部分解,也就是所有的颜色指派都没有冲突,则在当前节点处选择第一棵子树继续搜索,也就是为下一个顶点着颜色1,否则,对当前子树的兄弟子树继续搜索,也就是为当前顶点着色下一个颜色,如果所有m种颜色都已尝试过并且发生冲突,则回溯到当前节点的父结点处,上一个顶点的颜色被改变,以此类推。
对于下图中求解三着色问题,在解空间树中,从根节点出发,搜索第一棵子树,即为顶点A着颜色1,再搜索节点2的第一棵子树,即为顶点B着颜色1,这导致一个不可行解,回溯到节点2,选择节点2的第二棵子树,即为顶点B着颜色2,在为顶点C着色时,经过着颜色1和2的失败尝试后,选择节点4的第三棵子树,即为顶点C着颜色3,在节点7选择第一颗子树,就为顶点D着颜色1,但是在为顶点E着色时,顶点E无论着3种颜色的哪一种均发生冲突,于是导致回溯,在节点7选择第二棵子树也会发生冲突,于是,选择节点7的第三棵子树,即顶点D着颜色3,在节点10选择第一棵子树,即为顶点E着颜色1,得到了一个解(1,2,3,3,1)。注意到,解空间树中共有243个节点,而回溯法只搜索了其中的14个节点后就找到了问题的解。
- 416. 分割等和子集 - 中等 代码
哈密顿回路问题
要求从一个城市出发,经过每个城市恰好一次,然后回到出发城市。
下图(a)所示是一个无向图,在解空间树中从根结点1开始搜索。首先将x1值为1,到达结点2,表示哈密顿回路从顶点1开始。然后将x2置为1,到达结点3,但顶点1重复访问,搜索节点3的兄弟子树,将x2置为2,构成哈密顿回路的部分解(1,2),在经过节点5和节点6的失败尝试后,将x3置为3,将哈密顿回路的部分解扩展到(1,2,3),在经过节点8、节点9和节点10的失败尝试后,将x4置为4,将哈密顿回路的部分解扩展到(1,2,3,4),在经过节点12、节点13、节点14和节点15的失败的尝试后,将x5置为5,将哈密顿回路的部分解扩展到(1,2,3,4,5),但是在图(a)中从顶点5到顶点1没有边,引起回溯;将x4置为5,到达节点17,构成哈密顿回路的部分解(1,2,3,5),在经过节点18、19和20的失败的尝试后,将x5置为4,将哈密顿回路的部分解扩展到(1,2,3,5,4),而在图(a)中从顶点4到顶点1存在边,所以,找到了一条哈密顿回路(1,2,3,5,4,1),搜索过程结束。注意到,解空间树中共有243个节点,而回溯法只搜索了其中的21个节点后就找到了问题的解。在解空间树中的搜索构成如图(b)所示。
- 257. 二叉树的所有路径 - 简单 代码
组合问题中的回溯法
八皇后问题
八皇后问题是19世纪著名的数学家高斯与1850年提出来的。问题是:在8*8的棋盘上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
以使用回溯法计算四皇后问题举例。
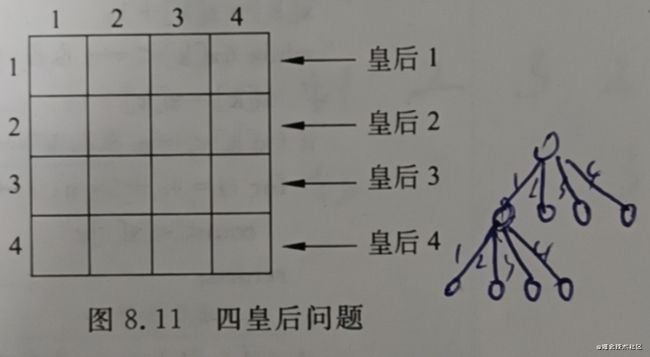
回溯法从空棋盘开始,首先把皇后1摆放到它所在行的第一个可能的位置,也就是第一行第一列;对于皇后2,在经过第一列和第二列的失败的尝试后,把它摆放到第一个可能的位置,也就是第二行第三列;对于皇后3,把它摆放到第三行的哪一列上都会引起冲突,所以,进行回溯,回到对皇后2的处理,把皇后2摆放到下一个可能的位置,也就是第二行第四列;然后,皇后3摆放到第三行的哪一列上都会引起冲突,再次进行回溯,回到对皇后2的处理,但此时皇后2位于棋盘的最后一列,继续回溯,回到对皇后1的处理,把皇后1摆放到下一个可能的位置,也就是第一行第二列,接下来,把皇后2摆放到第二行第四列的位置,把皇后3摆放到第三行第一列的位置,把皇后4摆放到第四行第三列的位置,这就是四皇后问题的一个解,在解空间树中的搜索过程如图所示。在n=4的情况下,解空间树共有65个节点,24个叶子节点,但实际搜索过程中,遍历操作只涉及8个节点,在24个叶子节点中,仅遍历一个叶子节点就找到了满足条件的解。
- 面试题 08.12. 八皇后 - 困难 代码
- 51. N 皇后 - 相同题目
- 52. N皇后 II - 相同题目
批处理作业调度问题
n个作业{1,2,……,n}要在两台机器上处理,每个作业必须先由机器1处理,然后再由机器2处理,机器1处理作业i所需时间为ai,机器2处理作业i所需时间为bi(1<=i<=n),批处理作业调度问题要求确定这n个作业的最优处理顺序,使得从第1个作业在机器1上处理开始,到最后一个作业在机器2上处理结束所需时间最少。
显然批处理作业的一个最优调度应使机器1没有空闲时间,且机器2的空闲时间最小。可以证明,存在一个最优作业调度,使得在机器1和机器2上作业以相同次序完成。
例如,有3个作业{1,2,3},这3个作业在机器1上所需的处理时间为(2,3,2),在机器2上所需的处理时间为(1,1,3),则这3个作业存在6种可能的调度方案:(1,2,3)、(1,3,2)、(2,1,3)、(2,3,1)、(3,1,2)、(3,2,1),相应的完成时间为10,8,10,9,8,8,如下图所示。显然,最佳调度方案是(1,3,2)、(3,1,2),其完成时间为8。
- 332. 重新安排行程 - 中等 代码
总结
回溯法解题一般有两种方式,递归和迭代。比较推荐递归的方式,相对于迭代,思路上更加容易理解。
回溯法其实就是深度优先遍历,整体比较简单,能够用来计算很多的问题,在计算过程中,如果有更多的剪枝条件,可能进一步加快计算出结果的速度。
本章讲述的几道题建议都写一下,每道题都不太一样,练完之后,中等难度的回溯法题目就没有太大问题。
最后
大家如果喜欢我的文章,可以关注我的公众号(程序员麻辣烫)
我的个人博客为:https://shidawuhen.github.io/
往期文章回顾:
算法
- 算法学习计划
- 蛮力法
- 分治法
- 减治法
- 动态规划法
- 贪心法
- 回溯法
技术
- 微服务之服务框架和注册中心
- Beego框架使用
- 浅谈微服务
- TCP性能优化
- 限流实现1
- Redis实现分布式锁
- Golang源码BUG追查
- 事务原子性、一致性、持久性的实现原理
- CDN请求过程详解
- 记博客服务被压垮的历程
- 常用缓存技巧
- 如何高效对接第三方支付
- Gin框架简洁版
- InnoDB锁与事务简析
读书笔记
- 敏捷革命
- 如何锻炼自己的记忆力
- 简单的逻辑学-读后感
- 热风-读后感
- 论语-读后感
- 孙子兵法-读后感
思考
- 对项目管理的一些看法
- 对产品经理的一些思考
- 关于程序员职业发展的思考
- 关于代码review的思考
- Markdown编辑器推荐-typora



