第四届“传智杯”初赛B组题解

文章目录

前言

A、组成成绩

题目描述

输入格式

输出格式

输入输出样例

输入 #1

B、报告赋分

题目描述

输入格式

输出格式

输入输出样例

C、竞争得分

题目描述

输入格式

输出格式

 输入输出样例

D、小卡与质数

题目背景

题目描述

输入格式

输出格式

输入输出样例

E、萝卜数据库

题目描述

输入格式

输出格式

输入输出样例

总结

---

前言

以下是本人参加传智杯B组初赛后写的相应题解。
 

---

A、组成成绩

题目描述

花栗鼠科技大学（Hualishu University of Science and Technology, HUST）的计算机组成原理快要出分了。你现在需要计算你的组原成绩如何构成。

具体来说，组原成绩分为三部分，分别是平时出勤 t，作业 h 和考试 e 。总成绩 w 由如下公式计算：

w=t×20%+h×30%+e×50%

其中我们保证  0  ≤ h, e, t ≤ 100

现在你知道了你的组原考试的 t, h, e，你希望计算你的总成绩。

由于教务系统的特殊性，最终成绩只能是整数，采取 直接去掉小数部分 的办法。

输入格式

一行三个整数，表示 t, h, e

输出格式

一行一个整数，为 w

输入输出样例

输入 #1

50 100 100

输出 #1 

90

#include 
using namespace std;

const int N = 100010; // 此处为本人习惯 不写也可
int t, h, e;

int main()
{
	cin >> t >> h >> e;
// 两种方式任选一种输出都可
//	printf("%d\n", int(t * 0.2 + h * 0.3 + e * 0.5));
	cout << int(t * 0.2 + h * 0.3 + e * 0.5) << endl; 
	return 0;
 } 

B、报告赋分

题目描述

花栗鼠科技大学的计算机组成原理实验最终的结课考核方式是提交一份报告。

然而作为任课老师，萝老师不希望大家过于内卷，所以指定了如下规定：

每份报告有一个卷面基础分 a。

在此基础上：

• 若是报告字数低于 16 页，则扣 10 分，如果分数低于 0 分了，则记作 0 分。

• 若是报告字数超过 20 页，每超过 1 页扣 1 分 ，直到分数扣到 0 分为止。

现在你知道了一份报告的卷面基础分 a 和它的页数 p ，请你计算这份报告的最终得分。我们保证 1 ≤ a ≤ 100,1 ≤ p ≤ 50.

输入格式

本题有多组数据。

第一行一个整数 T(1 ≤ T ≤ 1000) ，表示数据组数。

接下来 T 行，每行两个整数 a,p，意义如题所示。

输出格式

共 T 行，每行一个整数，表示该次询问的数据最终的得分。

输入输出样例

输入 #1 

2
70 17
80 10

 输出 #1

70
70

 

#include 
using namespace std;

const int N = 10010; // 此处为本人习惯 不写也可
int t, a, p;

int main()
{
	cin >> t;
	while (t --)
	{
		cin >> a >> p;
		if (p < 16)
			a -= 10;
		else if (p > 20)
			a -= p - 20;
		if (a < 0) cout << "0" << endl;
		else cout << a << endl;
	 } 
	 return 0;
} 

C、竞争得分

题目描述

为了鼓励大家写出更好的作业，花栗鼠科技大学（Hualishu University of Science and Technology, HUST）的组原实验采用了竞争得分的方式。

具体来说，假设有 n 个人提交了作业，并且其中原始得分最低的人记作 ，原始得分最高的人记作 ​，第 i 个人的原始得分为 ​，那么第 i 个人的得分就是：

 

由于成绩系统的问题，最终录入的成绩只能是整数，采用直接去掉小数部分的方法。

输入格式

第一行一个整数 n 表示人数。（ 1 ≤ n ≤ 1000）

第二行共 n 个整数，为序列 a ，其中  表示第 i 个人的原始作业得分。（1 ≤ ​ ≤ 1000）

输出格式

 一行，共 n 个整数，表示经过更新后每个人的得分。

 输入输出样例

输入 #1

3
1 2 3

输出 #1

0 50 100

D、小卡与质数

题目背景

小卡迷上了质数！

题目描述

小卡最近迷上了质数，所以他想把任何一个数都转化为质数！

小卡有 T 次询问，每次给你一个数字 x，问有多少个比 x 小的非负整数 y，使得 x⊕y 是质数，其中 ⊕ 表示按位异或。

输入格式

第一行一个正整数 T(1 ≤ T ≤ )，表示有 T 组询问。

接下来 T 行，每行一个正整数 x(1 ≤ x ≤ )。

输出格式

对于每组询问，输出一行一个整数，表示答案。

输入输出样例

输入 #1

9
5
6
7
8
9
10
100
1000
10000

 输出 #1

2
4
4
2
2
4
22
163
1132

#include 
#include 
#include 
using namespace std;

const int N = 2000010;
int n, t, cnt;  
int prime[N], st[N], a[N];

void sel_prime()
{
	// 这里用线性筛法将素数筛选出来 
	for (int i = 2; i <= N; i ++)
	{
		if (!st[i]) prime[cnt ++] = i;
		for (int j = 0; prime[j] <= N / i; j ++)
		{
			st[prime[j] * i] = 1;
			if (i % prime[j] == 0) break;
		}
	}
	// 将每个素数的以二进制最高位 1 所在的地方记录下来
	// 循环结束后的 a[i] 表示素数的二进制表示的最高位（第 i + 1 位）为 1 时素数的个数 
 
	for (int i = 0; i < cnt; i ++)
	{
		for (int j = 30; j >= 0; j --)
		{
			if (prime[i] >> j & 1)
			{
				a[j] ++;
				break;
			}
		}
	}
}
 
int main()
{
	cin >> t;
	sel_prime();
	while (t --)
	{
		cin >> n;  // 由于本人习惯， 将题目中要求的变量 x 命名为 n 
		int res = 0;
		/*  由于题目要求比 n 小的正整数(设为 y )与 n 异或后为质数，从二进制最高位（第 31 位）开始看：
			最高位为 0 , y 的最高位一定为 0 (满足比 n 小的条件).......一直往下判断.......到达 n 的最高有效位（此位一定为 1）
			最高有效位为 1，y的最高有效位为 0：
					结果的此位为 1 ，将以此位作为最高有效位的素数个数相加 （y 的最高位为 0，素数结果后面的数都可以通过 y 后面的数异或出来） 
			最高有效位为 1， y的最高有效位为 1：
					结果的此位为 0 ， 无作用 
			判断下一位
			下一位为 1 , y 的下一位为 0： 
					结果的此位为 1 ，将以此位作为最高有效位的素数个数相加 
			下一位为 1, y 的下一位为 1：
					结果的此位为 0，无作用
			下一位为 0, y 的下一位为 0
					结果的此位为 0，无作用
			下一位为 0, y 的下一位为 1
					此时不满足 y < n 这个条件 不会发生
			.........
			综上，将题目要求转换成 n 的二进制表示中 1 所在的位是多少素数的最高位， 将这些素数统计出来。 
			*/
		for (int j = 30; j >= 0; j --)
		{ 
			if (n >> j & 1)
				res += a[j]; 
		}
		cout << res << endl;
	}
}

E、萝卜数据库

 

题目描述

花栗鼠很喜欢偷吃生产队的大萝卜，因此花栗鼠科技大学正在研究一种新型的数据库，叫做萝卜数据库。

具体来说，它支持 k(1 ≤ k ≤ 100) 个字段，每个字段名都是整数，里面存储的数值也都是整数。

现在你支持如下操作：

• 向数据库中插入一个记录，它可能只会包含 k 个字段的某一部分。具体的操作格式详见“输入格式”。

• 在数据库中查询有多少条符合条件的记录。

现在你总共有 n 次操作（1 ≤ n ≤ 1000）,请你对每个回答操作，输出结果。

输入格式

第一行两个整数 n , k 意义如题所述。

接下来的若干行，每行代表一次操作，具体如下：

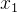
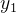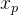
• 1 p  ​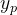,...,​   :表示一个插入操作，其中共有 p 个字段，第 i 字段的名字是 ​ ，值为 ​ .此处我们保证 1 ≤   ≤ k,1 ≤ ≤ 1000，并且    均为整数。 

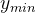
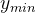• 2 x  ​：表示一次查询操作，表示查询所有满足 字段 x 的值在 [  ,​]  之间的记录有多少个。

输出格式

对于每个查询操作，输出一行一个整数，表示符合条件的记录个数。

输入输出样例

输入 #1

4 5
1 2 1 2 2 4
2 2 1 5
1 2 3 5 4 6
2 4 7 8

 输出 #1

1
0

#include 
using namespace std;

const int M = 110, N = 1010;
int a[N][M];
int n, k, op, p, x, y, y1, y2;
int r = 1, w = 1;

int main()
{
	cin >> n >> k;
	int t = n;
	while (n --)
	{
		cin >> op;
		if (op == 1)
		{
			cin >> p;

			for (int i = 0; i < p ; i ++)
			{
				cin >> x >> y;
				a[r][x] = y;
			}
			
			r ++;
		}
		else 
		{
			cin >> x;
			int cnt = 0;
			cin >> y1 >> y2;
			for (int i = 1; i <= r; i ++)
			{
				if (a[i][x] <= y2 && a[i][x] >= y1)
					cnt ++;
			}
			cout << cnt << endl;
		}
	}
	
	return 0;
}

---

总结

以上为本人，第一次写的题解， 不当之处，还请各位指正