正态分布的检验使用场景，以及 因子分析

变量的筛选和描述统计

1. 因子分析

因子分析法，其实质不是对数据进行数学变换，而是对于具有复杂相关关系的原始指标x1 x2···(P个)，通过寻找原始变量的共同方面来简化存在于原始变量之间的复杂关系，把各个测量本质相同的变量归入一个因子（公因子），这些公因子对原始变量起着重要的支配作用，公因子之间不相关，往往不可测，个数比原始变量个数少比如m个，是所有变量的共同具有的公共因素。即把原始评价指标化为m个公因子（综合指标），形成优化的指标体系。

正太分布的检验：
1 . Shapiro-Wilk检验只适用于小样本场合（3≤n≤50）
stats.shapiro(data)
X = ss.norm(0.1,3)
x_sample=X.rvs(10)
print(ss.shapiro(x_sample))
print(ss.normaltest(x_sample))
print(lillifors(x_sample))
print(ss.kstest(x_sample,‘norm’))

out:
(0.9038400053977966, 0.2412981241941452)
NormaltestResult(statistic=1.2055567870541868, pvalue=0.5472889377039196)
(0.18485067195130384, 0.2)
KstestResult(statistic=0.40882179882390696, pvalue=0.050385763915268056)

2. 20<样本数<50用normaltest算法检验正态分布性
   x_sample=X.rvs(40)
   print(ss.shapiro(x_sample))
   print(ss.normaltest(x_sample))
   print(lillifors(x_sample))
   print(ss.kstest(x_sample,‘norm’))
   stats.norm(data)

out:
(0.9814156293869019, 0.7418537735939026)
NormaltestResult(statistic=0.6389568338694439, pvalue=0.7265278829054929)
(0.10413829003266162, 0.2)
KstestResult(statistic=0.31463682457444525, pvalue=0.0005106744892731108)
3样本容量在【50，300】之间用lillifors
from statsmodels.stats.diagnostic import lillifors
x_sample=X.rvs(100)
print(ss.shapiro(x_sample))
print(ss.normaltest(x_sample))
print(lillifors(x_sample))
print(ss.kstest(x_sample,‘norm’))

out:
(0.9814156293869019, 0.7418537735939026)
NormaltestResult(statistic=0.6389568338694439, pvalue=0.7265278829054929)
(0.10413829003266162, 0.2)
KstestResult(statistic=0.31463682457444525, pvalue=0.0005106744892731108)
4 样本容量>300时候用KStest()
X= ss.norm(0.1,4)
x_sample=X.rvs(330)
print(ss.shapiro(x_sample))
print(ss.normaltest(x_sample))
print(lillifors(x_sample))
print(ss.kstest(x_sample,‘norm’,(0.1,4)))
print(ss.anderson(x_sample,dist=‘norm’))

out:
(0.9954125285148621, 0.4421331286430359)
NormaltestResult(statistic=0.4175156267354325, pvalue=0.8115917685208401)
(0.028580693044381433, 0.2)
KstestResult(statistic=0.04981302772324858, pvalue=0.37622873314529315)
AndersonResult(statistic=0.2778703332622854, critical_values=array([0.569, 0.648, 0.778, 0.907, 1.079]), significance_level=array([15. , 10. , 5. , 2.5, 1. ]))

3. 当数据不满足正太分布时候B0x-Cox转换

https://blog.csdn.net/sinat_26917383/article/details/77864582

**

• 正文：因子分析法

**
想要数据可以联系小编！

• 1 数据预处理
• 数据展示：

-import pandas as pd
#from sklearn.decomposition import FactorAnalysis
from sklearn.preprocessing import StandardScaler
from factor_analyzer import FactorAnalyzer
import seaborn as sns
import scipy.stats as ss
import numpy as np
data = pd.read_csv(‘data.csv’,index_col=0,encoding=‘utf-8’)
columns = [‘国有经济’,“集体经济单位”,“联合经济”, “股份制经济单位”, “外商业投资经济”, “港澳经济单位”,
“其他经济单位”]
data.loc[u’西藏’,‘x6’]=0
data.loc[u’青海’,‘x7’]=0
#中位数填充
data[‘x6’] = data[‘x6’].apply(lambda x:int(x))
data[‘x7’] = data[‘x7’].apply(lambda x:int(x))
data.loc[u’西藏’,‘x6’]=np.median(data[‘x6’])
data.loc[u’青海’,‘x7’]=np.median(data[‘x7’])
#data[‘x7’]
data.head()

分析数据是否有异常值（箱子上来）

sns.boxplot(np.sqrt(data.values[:,6]))
处理前的图：处理后的箱图：
直观看出是有异常值的；由于分析过程不符合正态分布，本文做了一下处理sqrt,似乎也不太好
正态分析：
for i in range(data.shape[1]):
print(ss.shapiro(np.log(data.values[:,i])))
print(ss.shapiro(data.values[:,i]))
print()

out:
(0.8478094935417175, 0.000455189379863441)
(0.797980546951294, 4.736970367957838e-05)

(0.9390956163406372, 0.07790136337280273)
(0.8727619051933289, 0.001610458712093532)

(0.9747883677482605, 0.6584002375602722)
(0.9111603498458862, 0.013848968781530857)

(0.9485302567481995, 0.14217382669448853)
(0.8903700113296509, 0.00417946046218276)

(0.9200542569160461, 0.02368474379181862)
(0.8051450848579407, 6.436666444642469e-05)

(0.9336402416229248, 0.05512480065226555)
(0.8290368914604187, 0.0001869533007266)

(0.9117269515991211, 0.014324542135000229)
(0.5315316915512085, 8.19287038211769e-09)
第一个不符合正态分布，最后一个也不符合，因为有异常值嘛！

标准化（本次标不标准似乎没有影响，但建议标准化）

检测是否适合做因子分析

1 指标1：

#Bartlett’s球形检验
from scipy.stats import bartlett
data_corr = data.corr() #np.corrcoef(data.values.T)
bartlett(data[‘x1’],data[‘x2’],data[‘x3’],data[‘x4’],data[‘x5’],data[‘x6’],data[‘x7’])

out
BartlettResult(statistic=97.76988654283352, pvalue=7.321875564618151e-19)
p值近似于零，符合。

KMO检验

import math
data_corr = data.corr()
def kmo(dataset_corr):
corr_inv = np.linalg.inv(dataset_corr)
nrow_inv_corr, ncol_inv_corr = dataset_corr.shape
A = np.ones((nrow_inv_corr,ncol_inv_corr))
for i in range(0,nrow_inv_corr,1):
for j in range(i,ncol_inv_corr,1):
A[i,j] = -(corr_inv[i,j])/(math.sqrt(corr_inv[i,i]*corr_inv[j,j]))
A[j,i] = A[i,j]
dataset_corr = np.asarray(dataset_corr)
kmo_num = np.sum(np.square(dataset_corr)) - np.sum(np.square(np.diagonal(A)))
kmo_denom = kmo_num + np.sum(np.square(A)) - np.sum(np.square(np.diagonal(A)))
kmo_value = kmo_num / kmo_denom
return kmo_value
print(kmo(data_corr))
#0.87适合做

fa = FactorAnalyzer()
fa.analyze(data=data,n_factors=2,rotation=‘varimax’)
fa.get_communalities()
#公因子共性

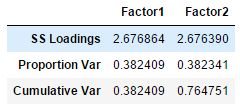
var = fa.get_factor_variance()
zhi
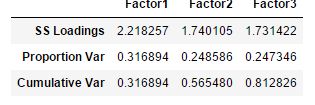
只能解释76%，应该是3个，

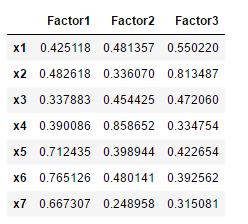
#成分矩阵
fa.loadings

得分：
score = fa.get_scores(data)
总得分：
得分
#score=( fac1 * fac1贡献率 + fac2 * fac2贡献率 + … + fac5 * fac5贡献率)/ 所有因子的累计贡献率
a = (score*var.values[1])/var.values[-1][-1]
a.head()

Full_score = a.sum(axis=1)
Full_score