数据结构与算法笔记六（树形dp，Morris遍历，大数据相关题目，位运算 ）

树形dp

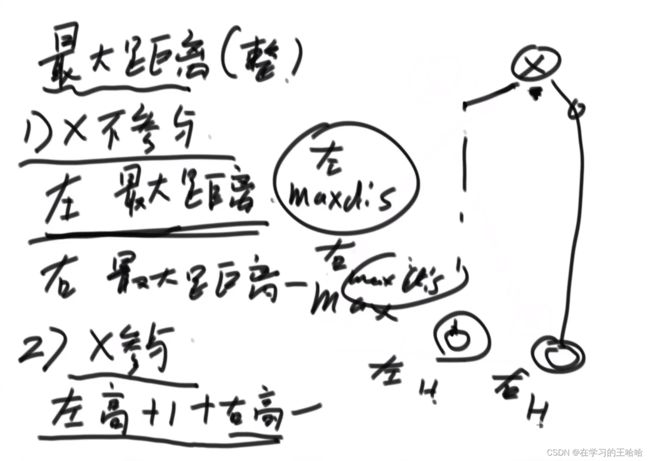
二叉树节点间的最大距离问题

leetcode543

可以分为头节点参与的和头节点不参与的，

头节点不参与：不经过头节点的。左树的最大距离，右数的最大距离。
头节点参与的：最大距离可能经过 头节点，左树最远的点到右树最远的点。 左高+1+右高

三者之间取最大值

排队的最大快乐值

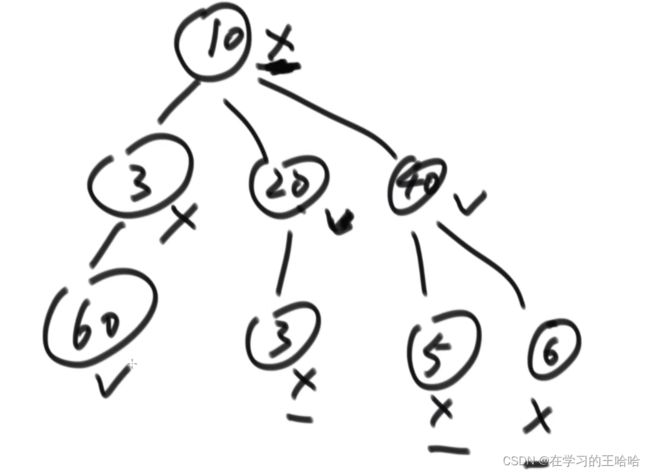
以x为头的整棵树快乐值是多少
x参与：x乐 + a的整棵树在a不来的情况下的最大快乐值 + 在b不来的情况下的最大快乐值 + 在c不来的情况下的最大快乐值
x不参与：0 + Max（a的整棵树在a来的情况下的最大快乐值，在a不来的情况下的最大快乐值 ）+max（b） + max(c )

package com.wanghaha.algorithm;

import java.util.List;

public class Day7_15_51MaxHappy {
    public static class Employee{
        public int happy;
        public List<Employee> nexts;
    }


    public static int maxHappy(Employee boss){
        Info headInfo = process(boss);
        return Math.max(headInfo.buMaxHappy, headInfo.laiMaxHappy);
    }

    public static class Info{
        public int laiMaxHappy;
        public int buMaxHappy;
        public Info(int laiMaxHappy, int buMaxHappy){
            this.buMaxHappy = buMaxHappy;
            this.laiMaxHappy = laiMaxHappy;
        }
    }

    public static Info process(Employee x){
        if(x.nexts.isEmpty()){  // x是基层员工的时候
            return new Info(x.happy, 0);
        }
        int lai = x.happy;
        int bu = 0;
        for (Employee next : x.nexts) {
            Info nextInfo = process(next);
            lai += nextInfo.buMaxHappy;
            bu += Math.max(nextInfo.laiMaxHappy,nextInfo.buMaxHappy );
        }
        return new Info(lai,bu);
    }

}

Morris遍历

当前节点如果有左树，一定会回到两次

每次都要遍历找到cur的左子树的右边界 时间复杂度不会上升
所有右边界都是不重复的

public static void morris(Node head){
        if(head == null){
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            mostRight = cur.left; // mostRight 是 cur的左孩子
            if( mostRight != null){
                while (mostRight.right != null && mostRight.right != cur){
                    mostRight = mostRight.right;
                }
                // mostRight 变成了cur的左子树上 最右的节点
                if(mostRight.right == null){
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                }else { // mostRight.right == cur
                    mostRight.right = null;
                }
            }
            cur = cur.right;

        }
    }

先序： 如果一个节点只到达一次，直接打印。如果一个节点到达两次，第一次打印

public static void morrisPre(Node head){
        if(head == null){
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            mostRight = cur.left; // mostRight 是 cur的左孩子
            if( mostRight != null){
                while (mostRight.right != null && mostRight.right != cur){
                    mostRight = mostRight.right;
                }
                // mostRight 变成了cur的左子树上 最右的节点
                if(mostRight.right == null){  // 第一次来到cur
                    System.out.print( cur.value + " ");
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                }else { // mostRight.right == cur
                    mostRight.right = null;
                }
            }else {
                System.out.print( cur.value + " ");
            }
            cur = cur.right;

        }
    }

中序：只有一次的节点，直接打印。 有两次的节点，第二次打印。

public static void morrisIn(Node head){
        if(head == null){
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            mostRight = cur.left; // mostRight 是 cur的左孩子
            if( mostRight != null){
                while (mostRight.right != null && mostRight.right != cur){
                    mostRight = mostRight.right;
                }
                // mostRight 变成了cur的左子树上 最右的节点
                if(mostRight.right == null){
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                }else { // mostRight.right == cur
                    mostRight.right = null;
                }
            }
            System.out.print(cur.value  + " ");
            cur = cur.right;

        }
    }

后序：把打印时机只放在能回到两次的节点。遇到第二次出现的节点，逆序打印自己左树的右边界。完了之后单独打印整棵树的右边界（逆序打印）

public static void morrisPos(Node head){
        if(head == null){
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            mostRight = cur.left; // mostRight 是 cur的左孩子
            if( mostRight != null){
                while (mostRight.right != null && mostRight.right != cur){
                    mostRight = mostRight.right;
                }
                // mostRight 变成了cur的左子树上 最右的节点
                if(mostRight.right == null){
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                }else { // mostRight.right == cur
                    mostRight.right = null;
                    printEdge(cur.left);
                }
            }
            cur = cur.right;
        }
        printEdge(head);
        System.out.println();
    }

如何逆序打印整棵树的右边界：单链表的逆序操作

//以X为头的树，逆序打印这棵树的右边界
    private static void printEdge(Node head) {
        Node tail = reverseEdge(head);
        Node cur = tail;
        while (cur != null) {
            System.out.print(cur.value + " ");
            cur = cur.right;
        }
        reverseEdge(tail);
    }

    public static Node reverseEdge(Node from) {
        Node pre = null;
        Node next = null;
        while (from != null) {
            next = from.right;
            from.right = pre;
            pre = from;
            from = next;
        }
        return pre;
    }

morris判断是否是搜索二叉树

package com.wanghaha.algorithm;

public class Day7_20_IsBSTwithMorris {
    public static boolean morris(Node head){
        if(head == null){
            return true;
        }
        Node cur = head;
        Node mostRight = null;
        int preValue = Integer.MIN_VALUE;
        while (cur != null) {
            mostRight = cur.left; // mostRight 是 cur的左孩子
            if( mostRight != null){
                while (mostRight.right != null && mostRight.right != cur){
                    mostRight = mostRight.right;
                }
                // mostRight 变成了cur的左子树上 最右的节点
                if(mostRight.right == null){
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                }else { // mostRight.right == cur
                    mostRight.right = null;
                }
            }
            if(cur.value <= preValue){
                return false;
            }
            preValue = cur.value;
            cur = cur.right;
        }
        return true;
    }
}

二叉树的递归套路和Morris如何选择？

如果必须做第三次信息的强整合，就是要想左树要信息，向右树要信息，然后在进行判断

如果需要遍历，依次判断，那么morris是最优解。

大数据相关题目解题技巧

利用分段统计的思想、并进一步节省大量空间

把范围做的位图对应，位图只需要用500M，

如果只给3kb的空间呢，找到一个未出现的数

先把3kb的内存生成一个 整形数组

申请一个长度为512的整形数组，把0~$2^{32}-1$这个范围分为512份，然后将40亿个数分别除以8388608，在512的那个范围上，就将该数+1，当计算完了后，一定会用某一范围的词频不够8388608个，然后 对这一范围的再分为512份，进行词频累加。
周而复始。就会找出哪一个没有出现的数

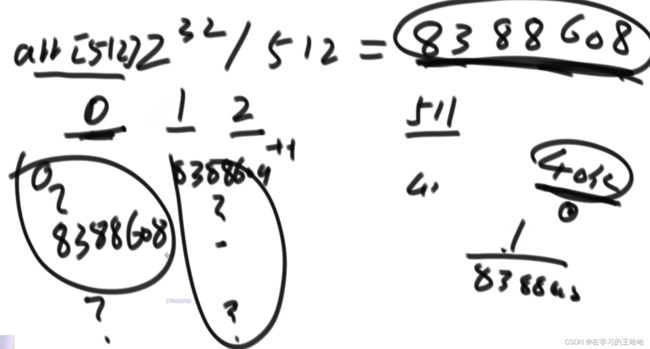
找出重复URL

布隆过滤器，
哈希函数分区

二维堆结构
补充问题解法：先进行分区，然后在小文件中使用哈希表，算出小文件中的top100，如何合并？使用堆

将所有小文件中的top100进行大根堆排序，然后将所有大根堆的堆顶拿出来，单独组成一个大根堆,称为总堆。弹出堆顶 就是全局最大的。 然后看弹出的堆顶是来自哪一个大根堆？然后将该大根堆的第二多的数 弹出到总堆里。
总堆就是将各个大根堆的最大的元素进行pk

找出所有出现了两次的数

不能使用哈希表，一个数4字节，词频 四字节，也就是一条记录8字节。 40亿个数会爆掉的

可以使用哈希分流然后在小文件中使用哈希表，然后再进行汇总。

也可以使用位图，位图可以表示一个数出现过，或者没有出现过。可以用两个位信息来代表该数的状态，00，01，10，11.
数的范围是0~$2^{32}-1$，如果想统计这个范围上所有i的数字，每个数用两个bit来表示它，则需要$（2^{32}-1）\ast 2$个bit， 所有需用$（2^{32}-1）\ast 2/8$byte字节，

补充问题：词频统计

10G文件，5G内存

10G的文件，每一个文件是一个有符号整数，无序的，如果只给你5G的内存，输出一个有序的10g文件。

堆的技巧

方法一： 整数+词频统计共占8字节，还有一些额外的内存消耗，就按16字节算,$2^4$，5G内存空间也就是$5\ast 2^{30}$byte,能存储 n = $2^{27}$个整数,然后将整数范围$-2^{31}到2^{31}$按n进行分区，共分为了$2^5$区，然后根据第一个分区对整个文件进行遍历，如果是该分区的数，就记录在小根堆中并且词频+1。周而复始。最后就有了从$-2^{31}到2^{31}$词频的数，然后将他们依次乘以词频放入在

方法二： 用大根堆存 用来存所有的数字中最小的n个数，此时y值等于小的数 ，输出一个文件后，y值等于输出的数最大的那个， 然后再遍历整个文件，忽略所有比y小的数

位运算的题目

给定两个有符号32位整数a和b，返回a和b中较大的。

getMax1有问题，a-b可能溢出

改进方法

a和b的符号相同，a-b一定不会溢出

判断一个32位正数是不是2的幂、4的幂

2的幂条件：2进制状态下只有一个1

方法1： num & (~num+1);
方法2：

4的幂：

第一步：先判断x是否只有一个1
第二步：1只能再0，2，4，8。。。位上， x& 0101010101！= 0 是4的幂

无符号实现加减乘除

leedcode375

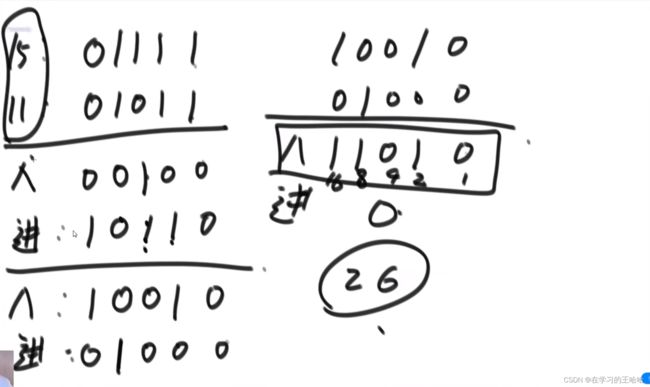
异或： 无进位相加
与： 如果要加的话，将产生进位信息
与运算向左移动一位： 就是进位信息

重复，直到进位信息都是0



减法： 就是a + b的相反数

b的相反数： b取反 + 1

乘法

>>>高位一定补0(逻辑右移)，>>右移负数时高位补的是1（算数右移）

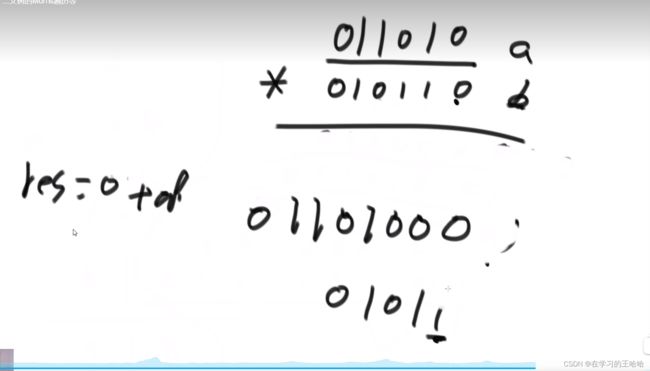
除法

b尽可能的向左移动，不要超过a
a-b不会减出负的

理解一：

理解二：


减掉后，让剩下的1再去试