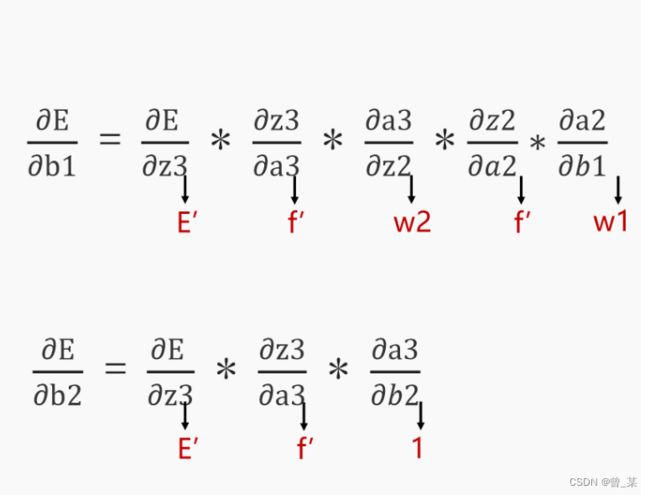BP神经网络与小波神经网络（附matlab代码,不用工具箱！）

一、神经网络介绍

        神经网络是模拟人脑神经元传递信息的一种方式来进行数据特征的一个学习，其特点为：具有非线性映射能力；不需要精确的数学模型；擅长从输入输出数据中学习有用的知识；容易实现并行运算；由大量简单计算单元组成。

        现在已经出现了许多神经网络模型及相应的学习算法。其中BP神经网络的误差反向传播学习算法是一种最常用的神经网络算法。它利用输出后的误差来估计输出层的直接前导层的误差，在利用这个误差估计更前一层的误差，如此一层一层的反传下去，就获得了所有层的误差估计。

二、BP神经网络的原理

大家可以参考这篇文章以及他的视屏来了解，这里只引用其关键信息。https://blog.csdn.net/weixin_56619527/article/details/122483942

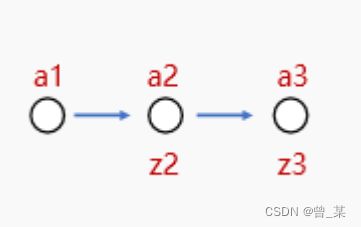
下面这个可以表示为一个简单的3层神经网络。

其x作为数据的传递过程如下图所示。

好了，上图已经完成了一个数据的前向传递，那么如何进行误差反馈呢？下面两幅图给出你答案。

其是利用求导的链式法则来进行说明的，很容易理解，其大部分博主都是利用矩阵去进行一个梯度下降，导致许多人不懂其内涵，通过矩阵运算感觉导的没有什么感觉了，因此我不采用批量求导，而是对每一个权重进行求导的方式；这里推荐大家先把神经网络的结构图先画出来，然后在去看代码，容易理解一些。

三、代码详解

首先进行一个数据的导入，采用波士顿房价数据集进行输入，有相关性大小选取前面最大的3个自变量作为输入，房价作为输出。

clear all;
close all;
clc
%读取数据
reference=xlsread('house_data.csv');
rowrank1=randperm(size(reference,1));%打乱列数
reference=reference(rowrank1,:);
input=reference(:,[6,11,13]);
output=reference(:,14);

       下面就是要进行一个网络结构的搭建和权值的初始化了，其中n代表隐含层的节点个数，M代表输入的变量个数，N代表数的因变量的个数，因此形成了wjk一个6*3，wij一个1*6，b1一个1*6，b2一个1*1的矩阵，还设置的最大迭代次数和学习率。

M=size(input,2); %输入节点个数
N=size(output,2); %输出节点个数

n=6; %隐形节点个数
lr1=0.01; %学习概率
lr2=0.001; %学习概率
maxgen=100; %迭代次数

%权值初始化
Wjk=randn(n,M);Wjk_1=Wjk;Wjk_2=Wjk_1;
Wij=randn(N,n);Wij_1=Wij;Wij_2=Wij_1;
b1=randn(1,n);b1_1=b1;b1_2=b1_1;
b2=randn(1,N);b2_1=b2;b2_2=b2_1;

       这里的y是为了存储输出的结果值以便于和实际值作比较，net和net_ab都是一个1*6的矩阵，显然是为了存储与隐含层相关的一些值的。

%节点初始化
y=zeros(1,N);
net=zeros(1,n);
net_ab=zeros(1,n);

下面是为了初始化权重梯度和规定一些学习的参数，由于我们这里是对每个参数进行求导所以初始化权重梯度的意义就是为了解决一些中间变量的值，最后还是要归零的，以不妨碍下一次的梯度下降。

%权值学习增量初始化
d_Wjk=zeros(n,M);
d_Wij=zeros(N,n);
d_b1=zeros(1,n);
d_b2=zeros(1,N);

%学习率
xite=0.01;
alfa=0.01;
yn1=zeros(1,506);

       下面是对原始数据的归一化操作，是数据更为集中，梯度的下降更为容易，数据拜托了量纲的影响，其归一化的优点就不用我多说了。y1视为存储输出值为了画图和实际值比较。

%% 输入输出数据归一化
[inputn,inputps]=mapminmax(input');
[outputn,outputps]=mapminmax(output'); 
inputn=inputn';
outputn=outputn';
error=zeros(1,maxgen);
y1=zeros(1,506);

       下面开始训练，外循环为最大迭代次数，然后根据数据数量进行挨个训练。x为提取到的自变量，yqw为提取的实际值。

%% 开始训练
for i=1:maxgen
    
    %误差累计
    error(i)=0;
    
    % 循环训练
    for kk=1:size(input,1)
        x=inputn(kk,:);
        yqw=outputn(kk,:);

外循环为选定一个隐含层节点，内循环为每个输入量乘以该节点的与输入节点的权重，得到该节点的求和值net（j）

 for j=1:n
            for k=1:M
                net(j)=net(j)+Wjk(j,k)*x(k);
            end

下面就是加上阀值和进行激活

net_ab(j)=net(j)+b1(j);
temp=sigmoid(net_ab(j));

       下面就是该节点与输出节点的权值进行相乘，得到输出值，这里是回归问题，其输出不用激活函数。

 for k=1:N
     y(k)=y(k)+Wij(k,j)*temp;   
 end
end
  for kw=1:N
     y(kw)=y(kw)+b2(kw);
  end

下面这个就是求一下误差和了

y1(kk)=y;
%计算误差和
error(i)=error(i)+sum(abs(yqw-y));

好了上面已经把前向传播给完成了，现在进行一个最重要的权重值的调整，大循环还是以隐含层的节点数，这里一次内循环就可以求出一个隐含层节点到一个输出节点的权重。

for j=1:n
   %计算d_Wij
   temp=sigmoid(net_ab(j));
   for k=1:N
       d_Wij(k,j)=d_Wij(k,j)-(yqw(k)-y(k))*temp;
   end

下面就是求输入节点到隐含层节点的权重梯度

temp=d_sigmoid(net_ab(j));
for k=1:M
    for l=1:N
        d_Wjk(j,k)=d_Wjk(j,k)-(yqw(l)-y(l))*Wij(l,j) ;
    end
        d_Wjk(j,k)=d_Wjk(j,k)*temp*x(k);
end

下面就比较简单了，是对2个阀值的一个更新

for k=1:N
    d_b2(k)=d_b2(k)-(yqw(k)-y(k))
end
%计算d_b1
for k=1:N
    d_b1(j)=d_b1(j)-(yqw(k)-y(k))*Wij(k,j);
end
    d_b1(j)=d_b1(j)*temp;
end

最后进行一个权重更新和一个绘图处理

 Wij=Wij-lr1*d_Wij;
        Wjk=Wjk-lr1*d_Wjk;
        b1=b1-lr2*d_b1;
        b2=b2-lr2*d_b2;
    
        d_Wjk=zeros(n,M);
        d_Wij=zeros(N,n);
        d_b1=zeros(1,n);
        d_b2=zeros(1,N);

        y=zeros(1,N);
        net=zeros(1,n);
        net_ab=zeros(1,n);
        
        Wjk_1=Wjk;Wjk_2=Wjk_1;
        Wij_1=Wij;Wij_2=Wij_1;
        b1_1=b1;b1_2=b1_1;
        b2_1=b2;b2_2=b2_1;
    end
end
ynn=mapminmax('reverse',y1,outputps);
figure
plot(output,'r')
xlabel('对应的索引信息')
ylabel('房价'); %设置纵坐标轴
title('波士顿房价预测'); %标题
%legend('注释'); %图形注释
axis([0,500,0,55]);%x,y轴的范围
hold on
plot(ynn,'g')

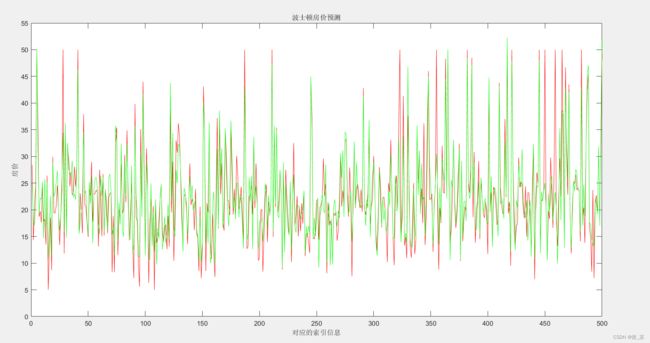
下面是运行的结果

下面是总的代码，供给大家参考，如果觉得可以请点一下赞，刚来需要流量继续更新

clear all;
close all;
clc

%读取数据
reference=xlsread('house_data.csv');
rowrank1=randperm(size(reference,1));%打乱列数
reference=reference(rowrank1,:);
input=reference(:,[6,11,13]);
output=reference(:,14);
M=size(input,2); %输入节点个数
N=size(output,2); %输出节点个数

n=6; %隐形节点个数
lr1=0.01; %学习概率
lr2=0.001; %学习概率
maxgen=100; %迭代次数

%权值初始化
Wjk=randn(n,M);Wjk_1=Wjk;Wjk_2=Wjk_1;
Wij=randn(N,n);Wij_1=Wij;Wij_2=Wij_1;
b1=randn(1,n);b1_1=b1;b1_2=b1_1;
b2=randn(1,N);b2_1=b2;b2_2=b2_1;

%节点初始化
y=zeros(1,N);
net=zeros(1,n);
net_ab=zeros(1,n);

%权值学习增量初始化
d_Wjk=zeros(n,M);
d_Wij=zeros(N,n);
d_b1=zeros(1,n);
d_b2=zeros(1,N);

%学习率
xite=0.01;
alfa=0.01;
yn1=zeros(1,506);
%% 输入输出数据归一化
[inputn,inputps]=mapminmax(input');
[outputn,outputps]=mapminmax(output'); 
inputn=inputn';
outputn=outputn';
error=zeros(1,maxgen);
y1=zeros(1,506);
%% 开始训练
for i=1:maxgen
    
    %误差累计
    error(i)=0;
    
    % 循环训练
    for kk=1:size(input,1)
        x=inputn(kk,:);
        yqw=outputn(kk,:);
   
        for j=1:n
            for k=1:M
                net(j)=net(j)+Wjk(j,k)*x(k);
            end
            net_ab(j)=net(j)+b1(j);
            temp=sigmoid(net_ab(j));
            for k=1:N
                y(k)=y(k)+Wij(k,j)*temp;   
            end
        end
        for kw=1:N
            y(kw)=y(kw)+b2(kw);
        end
        y1(kk)=y;
        %计算误差和
        error(i)=error(i)+sum(abs(yqw-y));
        
        %权值调整
        for j=1:n
            %计算d_Wij
            temp=sigmoid(net_ab(j));
            for k=1:N
                d_Wij(k,j)=d_Wij(k,j)-(yqw(k)-y(k))*temp;
            end
            %计算d_Wjk
            temp=d_sigmoid(net_ab(j));
            for k=1:M
                for l=1:N
                    d_Wjk(j,k)=d_Wjk(j,k)-(yqw(l)-y(l))*Wij(l,j) ;
                end
                d_Wjk(j,k)=d_Wjk(j,k)*temp*x(k);
            end
            %计算d_b2
            for k=1:N
                d_b2(k)=d_b2(k)-(yqw(k)-y(k));
            end
            
            %计算d_b1
            for k=1:N
                d_b1(j)=d_b1(j)-(yqw(k)-y(k))*Wij(k,j);
            end
            d_b1(j)=d_b1(j)*temp;
        end
        
        %权值参数更新      
        Wij=Wij-lr1*d_Wij;
        Wjk=Wjk-lr1*d_Wjk;
        b1=b1-lr2*d_b1;
        b2=b2-lr2*d_b2;
    
        d_Wjk=zeros(n,M);
        d_Wij=zeros(N,n);
        d_b1=zeros(1,n);
        d_b2=zeros(1,N);

        y=zeros(1,N);
        net=zeros(1,n);
        net_ab=zeros(1,n);
        
        Wjk_1=Wjk;Wjk_2=Wjk_1;
        Wij_1=Wij;Wij_2=Wij_1;
        b1_1=b1;b1_2=b1_1;
        b2_1=b2;b2_2=b2_1;
    end
end
ynn=mapminmax('reverse',y1,outputps);
figure
plot(output,'r')
xlabel('对应的索引信息')
ylabel('房价'); %设置纵坐标轴
title('波士顿房价预测'); %标题
%legend('注释'); %图形注释
axis([0,500,0,55]);%x,y轴的范围
hold on
plot(ynn,'g')


function y=d_sigmoid(t)

S=1/(1+exp(t));
y=S*(1-S);



function y=sigmoid(t)

y=1/(1+exp(t));

小波变换的神经网络我这里就不必多费口舌了，下面给出WNN的运行结果图

其效果是要比普通的神经网络要好的；其具体代码和数据集，我完善过后在进行一个上传

小波神经网络与BP神经网络（matlab不用工具箱带数据集）-机器学习文档类资源-CSDN文库