【数据结构】堆排序的实现
目录
1.向上调整算法 O(N*logN)
2.向下调整算法 O(N)
3.堆排序 O(N*logN)
3.1比较建堆排序和直接堆排序
3.2堆排序思想:
3.2.1.首先在a这个数组中直接建堆
3.2.2 排升序用大堆,降序用小堆
3.3堆排序完整代码
4.堆排序中建堆的时间复杂度的证明
堆是一个完全二叉树
假设在这个堆中高度为K层,总节点数为N
那么由 2^K-1=N 得到 log(N+1)=K
1.向上调整算法 O(N*logN)
在堆插入数据时使用
//向上调整
void AdjustUp(int* a, int child)//从孩子的位置向上调整
{
int parent = (child - 1) / 2;
//请注意(-1)/2=0 所以不能用parent>=0作为判断方式
while (child > 0)//child到0就不用交换了
{
if (a[parent] > a[child])
{
swap(&a[parent], &a[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}2.向下调整算法 O(N)
在堆删除数据的时候使用,本质是找出次大或者次小
前提是左右子树都需要同时是大堆或者小堆
void AdjustDown(int* a, int size,int parent)//从父亲的位置向下调整
{
assert(a);
int minchild = parent * 2 + 1;
while (minchild < size)
{
if (minchild + 1 < size)
{
if (a[minchild] > a[minchild + 1])//找到较小的子节点
{
minchild = minchild + 1;
}
}
if (a[parent] > a[minchild])//条件满足,和较小的子节点交换位置
{
swap_(&a[parent], &a[minchild]);
parent = minchild;
minchild = parent * 2 + 1;
}
else
{
break;
}
}
}
3.堆排序 O(N*logN)
3.1比较建堆排序和直接堆排序
前提:这个排序需要让数组本身有序。
如果直接使用实现的堆这个数据结构,空间复杂度为O(N)
建堆排序——————————————————
1.建堆排序不是对这个数组处理,是会在堆中会额外开辟一片空间,从这个数组中拿数据。
可以写一个循环每次拿一个。
2.然后在其中建好堆之后(请注意堆中的数据不是有序的),开始取堆顶的数据,取堆顶数据时,方法需要把堆顶数据和最后一个数据进行交换,取最后一个数据,然后对于现在的第一个元素利用向下调整算法,重新调整。
3.这样每次堆顶的数据都是比较前一个次小或者次大的,需要这样依次取出按顺序放入原先数组中,才能完成排序。
堆排序——————————————————
实际当中堆排序,会传一个数组给这个排序函数,不会额外开辟一片空间。
void HeapSort(int* a, int n);
3.2堆排序思想:
把这个数组本身转化成一个堆,利用堆的性质进行排序。
3.2.1.首先在a这个数组中直接建堆
1.向下调整建堆O(N)————————————
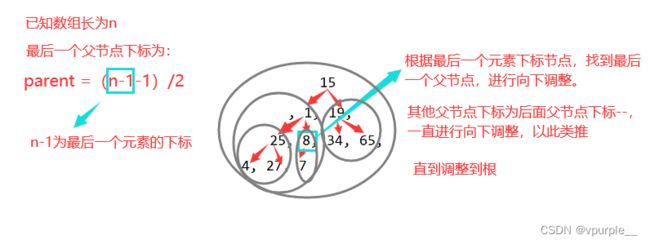
向下调整有前提,必须左右子树都是小堆或者大堆才可以。可以从倒数第一个非叶节点(就是最后一个节点的父节点),开始向下调整建堆。
根据父节点的下标关系,调整完一个后下标--,找到前一个父节点,继续进行向下调整,以此类推。
如下所示:
//建堆 向下调整
for (parent = (n - 1 - 1) / 2; parent >= 0; parent--)
{
AdjustDown_(a, n, parent);
}2.向上调整建堆O(N*logN)———————————
利用直接插入的思想,模拟插入过程进行尾插+向上调整。
int child = 0;
for (child = 0; child < n; child++)
{
AdjustUp(a, child);
}
3.2.2 排升序用大堆,降序用小堆
堆排序本质是一种选择排序,找到最大的元素之后要考虑如何选次小的元素。
堆排序时要利用堆排序本身的优势,它的父子节点的关系。
以降序为例:
1.建小堆
2.第一个和最后一个元素进行位置交换,把最后一个元素不看做堆中的元素向下调整,选出次小的,以此类推
//以排降序为例
//交换位置,最小放最后,然后向下调整变成小根堆
for (int i = 0; i < n; i++)
{
int last = n -1 - i;
swap(&a[0], &a[last]);//交换第一个元素和最后一个元素
AdjustDown(a, last, 0);//向下调整
}3.3堆排序完整代码
#include
#include
//交换
void swap_(int* a, int* b)
{
int tmp = 0;
tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustDown_(int* a, int size,int parent)//从孩子的位置向下调整
{
assert(a);
int minchild = parent * 2 + 1;
while (minchild < size)
{
if (minchild + 1 < size)
{
if (a[minchild] > a[minchild + 1])//找到较小的子节点
{
minchild = minchild + 1;
}
}
if (a[parent] > a[minchild])//条件满足,和较小的子节点交换位置
{
swap_(&a[parent], &a[minchild]);
parent = minchild;
minchild = parent * 2 + 1;
}
else
{
break;
}
}
}
// 对数组进行堆排序
void HeapSort(int* a, int n)
{
//向下调整排序
//排降序,小根堆
int parent = 0;
//建堆 向下调整
for (parent = (n - 1 - 1) / 2; parent >= 0; parent--)
{
AdjustDown_(a, n, parent);
}
//交换位置,最小放最后,然后向下调整变成小根堆
for (int i = 0; i < n; i++)
{
int last = n -1 - i;
swap_(&a[0], &a[last]);
AdjustDown_(a, last, 0);
}
}
4.堆排序中建堆的时间复杂度的证明
以满二叉树的结构来计算
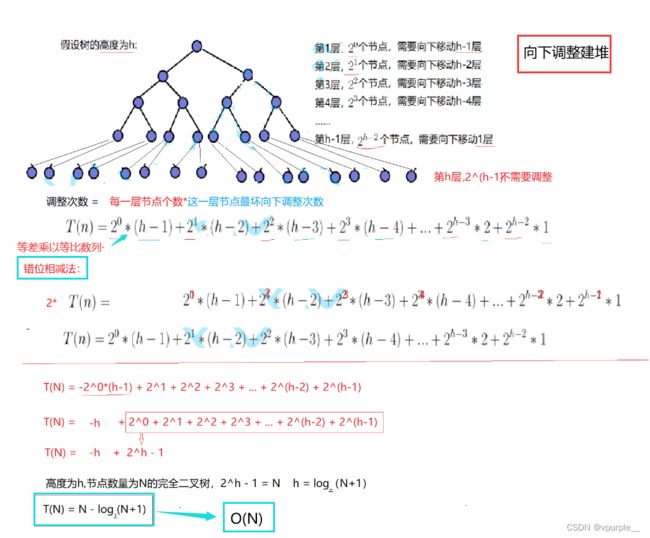
4.1.向下调整建堆 O(N)
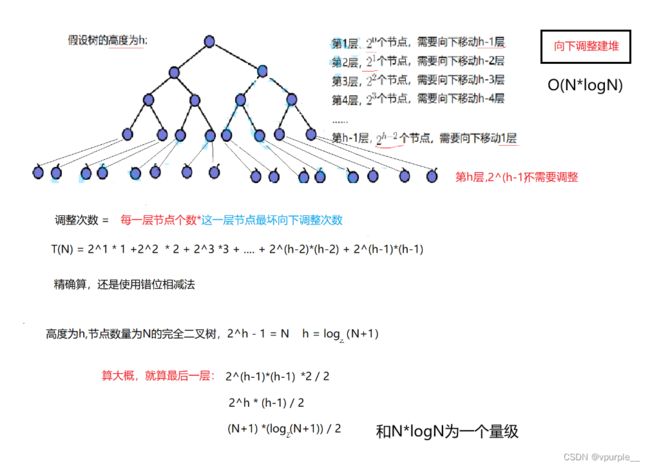
4.2.向上调整建堆 O(N*logN)
你好,这里是媛仔与难搞的堆排序……整理下来感觉还是对于堆排序不够熟练,还是要多多练习啊。希望这篇文章对你能够有所帮助,也欢迎和我多多交流!!我们下一篇见~