力扣二叉树简单题集合(Java)
- 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
class Solution {
int count;
public int diameterOfBinaryTree(TreeNode root) {
count = 1;
depth(root);
return count-1;
}
public int depth(TreeNode root){
if(root== null) return 0;
int L = depth(root.left);
int R = depth(root.right);
count = Math.max(count,L+R+1);
return Math.max(L,R) +1;
}
}
- 二叉树的坡度
给定一个二叉树,计算 整个树 的坡度 。
一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为 0 ;没有右子树的话也是一样。空结点的坡度是 0 。
整个树 的坡度就是其所有节点的坡度之和。
输入:root = [4,2,9,3,5,null,7]
输出:15
解释:
节点 3 的坡度:|0-0| = 0(没有子节点)
节点 5 的坡度:|0-0| = 0(没有子节点)
节点 7 的坡度:|0-0| = 0(没有子节点)
节点 2 的坡度:|3-5| = 2(左子树就是左子节点,所以和是 3 ;右子树就是右子节点,所以和是 5 )
节点 9 的坡度:|0-7| = 7(没有左子树,所以和是 0 ;右子树正好是右子节点,所以和是 7 )
节点 4 的坡度:|(3+5+2)-(9+7)| = |10-16| = 6(左子树值为 3、5 和 2 ,和是 10 ;右子树值为 9 和 7 ,和是 16 )
坡度总和:0 + 0 + 0 + 2 + 7 + 6 = 15
思路
public int findTilt(TreeNode root) {
int count = getval(root);
return count;
}
public int getval(TreeNode root){
if(root.left == null && root.right == null) return 0;
if(root != null){
int val =Math.abs(root.left.val - root.right.val);
}
int lval = getval(root.left);
int rval = getval(root.right);
return lval +rval;
}
class Solution {
private int res = 0;
public int findTilt(TreeNode root) {
dfs(root);
return res;
}
/**
* 返回以该node为根的树的所有节点和
*/
public int dfs(TreeNode node) {
if (node == null) return 0;
int leftSum = dfs(node.left);
int rightSum = dfs(node.right);
res += Math.abs(leftSum - rightSum);
return leftSum + rightSum + node.val;
}
}
- 另一个树的子树
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
示例 1:
给定的树 s:
3
/
4 5
/
1 2
给定的树 t:
4
/
1 2
返回 true,因为 t 与 s 的一个子树拥有相同的结构和节点值。
思路
public boolean isSubtree(TreeNode s, TreeNode t) {
if(s == null && t == null) return true;
if(s != null && t == null) return true;
if(s == null && t != null) return false;
if(t.val == s.val){
isSubtree(s.left,t.left);
isSubtree(s.right,t.right);
return true;
}else{
isSubtree(s.left,t);
isSubtree(s.right,t);
return true;
}
return false;
}
class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
return dfs(s, t);
}
public boolean dfs(TreeNode s, TreeNode t) {
if (s == null) {
return false;
}
return check(s, t) || dfs(s.left, t) || dfs(s.right, t);
}
public boolean check(TreeNode s, TreeNode t) {
if (s == null && t == null) {
return true;
}
if (s == null || t == null || s.val != t.val) {
return false;
}
return check(s.left, t.left) && check(s.right, t.right);
}
}
- 根据二叉树创建字符串
你需要采用前序遍历的方式,将一个二叉树转换成一个由括号和整数组成的字符串。空节点则用一对空括号 “()” 表示。而且你需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1:
输入: 二叉树: [1,2,3,4]
1
/
2 3
/
4
输出: “1(2(4))(3)”
解释: 原本将是“1(2(4)())(3())”,
在你省略所有不必要的空括号对之后,
它将是“1(2(4))(3)”。
除了我们不能省略第一个对括号来中断输入和输出之间的一对一映射关系。
示例 2:
输入: 二叉树: [1,2,3,null,4]
1
/
2 3
\
4
输出: “1(2()(4))(3)”
解释: 和第一个示例相似,
除了我们不能省略第一个对括号来中断输入和输出之间的一对一映射关系。
思路
public String tree2str(TreeNode t) {
StringBuffer sb = new StringBuffer();
if(t == null) return sb.toString();
sb.append(t);
if(t.left !=null){
sb.append("(");
tree2str(t.left);
sb.append(")");
}
if(t.right != null){
sb.append("(");
tree2str(t.right);
sb.append(")");
}
return sb.toString();
}
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public String tree2str(TreeNode t) {
if(t==null)
return "";
if(t.left==null && t.right==null)
return t.val+"";
if(t.right==null)
return t.val+"("+tree2str(t.left)+")";
return t.val+"("+tree2str(t.left)+")("+tree2str(t.right)+")";
}
}
- 合并二叉树
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出:
合并后的树:
3
/
4 5
/ \ \
5 4 7
注意: 合并必须从两个树的根节点开始。
思路
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
TreeNode root = null;
if(t1 == null && t2 == null) return root;
return dfs(root,t1,t2);
}
public TreeNode dfs(TreeNode root, TreeNode t1,TreeNode t2){
if(t1 != null || t2 != null ){
root.val = t1.val + t2.val;
}
dfs(root,t1.left,t2.left);
dfs(root,t1.right,t2.right);
return root;
}
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
if(t1 == null){
return t2;
}
if(t2 == null){
return t1;
}
TreeNode root = new TreeNode(t1.val + t2.val);
root.left = mergeTrees(t1.left,t2.left);
root.right = mergeTrees(t1.right,t2.right);
return root;
}
}
- 二叉树的层平均值
给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
示例 1:
输入:
3
/
9 20
/
15 7
输出:[3, 14.5, 11]
解释:
第 0 层的平均值是 3 , 第1层是 14.5 , 第2层是 11 。因此返回 [3, 14.5, 11] 。
广度优先搜索
public List<Double> averageOfLevels(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<TreeNode>();
List<Double> res = new ArrayList<>();
queue.offer(root);
while(!queue.isEmpty()){
double sum =0.0;
int size = queue.size();
for(int i =0; i<size;i++){
TreeNode node = queue.poll();
sum += node.val;
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
res.add(sum/size);
}
return res;
}
- 两数之和 IV - 输入 BST
给定一个二叉搜索树和一个目标结果,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
案例 1:
输入:
5
/
3 6
/ \
2 4 7
Target = 9
输出: True
案例 2:
输入:
5
/
3 6
/ \
2 4 7
Target = 28
输出: False
public class Solution {
public boolean findTarget(TreeNode root, int k) {
Set < Integer > set = new HashSet();
return find(root, k, set);
}
public boolean find(TreeNode root, int k, Set < Integer > set) {
if (root == null)
return false;
if (set.contains(k - root.val))
return true;
set.add(root.val);
return find(root.left, k, set) || find(root.right, k, set);
}
}
- 二叉树中第二小的节点
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。更正式地说,root.val = min(root.left.val, root.right.val) 总成立。给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。
示例 1:
输入:root = [2,2,5,null,null,5,7]
输出:5
解释:最小的值是 2 ,第二小的值是 5 。
思路
public int findSecondMinimumValue(TreeNode root) {
if(root == null) return -1;
int [] res = new int[2];
res[0] = root.val;
res[1] = root.left.val;
res[2] = root.right.val;
if(res[1]< res[2]){
return res[2];
}else if(res[1] > res[2]){
return res[1];
}else{
return -1;
}
return -1;
}
public int findSecondMinimumValue(TreeNode root) {
if (root == null) return -1;
return help(root, root.val);
}
private int help(TreeNode root, int min) {
if (root == null) return -1;
if (root.val > min) return root.val;
int left = help(root.left, min);
int right = help(root.right, min);
if (left == -1) return right;
if (right == -1) return left;
return Math.min(left, right);
}
-
二叉搜索树节点最小距离
给定一个二叉搜索树的根节点 root,返回树中任意两节点的差的最小值。
示例:
输入: root = [4,2,6,1,3,null,null]
输出: 1
解释:
注意,root是树节点对象(TreeNode object),而不是数组。
给定的树 [4,2,6,1,3,null,null] 可表示为下图:4/
2 6
/ \
1 3
最小的差值是 1, 它是节点1和节点2的差值, 也是节点3和节点2的差值。
思路
public int minDiffInBST(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
minDiff(res, root);
int size = res.size();
int[] re = new int[size];
int min =Integer.MAX_VALUE;
for(int i =0;i < size;i++){
int j =i+1;
if(j <size){
int m= re[j] - re[i];
min = Math.min(min,m);
}
}
return min;
}
public void minDiff(ArrayList<Integer> res ,TreeNode root){
TreeNode node = root;
res.add(node.val);
if(node.left != null){
minDiff(res,node.left);
}
if(node.right != null){
minDiff(res,node.right);
}
}
public int minDiffInBST(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
minDiff(res, root);
int min = Integer.MAX_VALUE;
Collections.sort(res);
for (int i = 0; i < res.size() - 1; ++i)
min = Math.min(min, res.get(i+1) - res.get(i));
return min;
}
public void minDiff(ArrayList<Integer> res ,TreeNode root){
TreeNode node = root;
res.add(node.val);
if(node.left != null){
minDiff(res,node.left);
}
if(node.right != null){
minDiff(res,node.right);
}
}
}
- 叶子相似的树
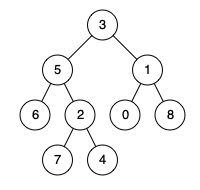
请考虑一棵二叉树上所有的叶子,这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。举个例子,如上图所示,给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。如果有两棵二叉树的叶值序列是相同,那么我们就认为它们是 叶相似的.如果给定的两个头结点分别为 root1 和 root2 的树是叶相似的,则返回 true;否则返回 false 。
示例 1:
输入:root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8]
输出:true
思路
public boolean leafSimilar(TreeNode root1, TreeNode root2) {
if(root1.val == root2.val) return true;
if(root1.val != root2.val) return false;
if((root1.left == null) && (root1.right == null) && (root2.left == null )&& (root2.right == null) &&(root1.val = root2.val)){
return true;
}
return leafSimilar(root1.left,root2.left) && leafSimilar(root1.right,root2.right);
}
public boolean leafSimilar(TreeNode root1, TreeNode root2) {
ArrayList<Integer> res1 = new ArrayList<Integer>();
ArrayList<Integer> res2 = new ArrayList<Integer>();
leaf(root1,res1);
leaf(root2,res2);
return res1.equals(res2);
}
public void leaf(TreeNode node, ArrayList<Integer> res){
if(node != null){
if(node.left == null && node.right == null){
res.add(node.val);
}
leaf(node.left,res);
leaf(node.right,res);
}
}
- 递增顺序查找树
给你一个树,请你 按中序遍历 重新排列树,使树中最左边的结点现在是树的根,并且每个结点没有左子结点,只有一个右子结点。
示例 :
输入:[5,3,6,2,4,null,8,1,null,null,null,7,9]
5
/ \
3 6
/ \ \
2 4 8
/ / \
1 7 9
输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
1
\
2
\
3
\
4
\
5
\
6
\
7
\
8
\
9
class Solution {
public TreeNode increasingBST(TreeNode root) {
List<Integer> vals = new ArrayList();
inorder(root, vals);
TreeNode ans = new TreeNode(0), cur = ans;
for (int v: vals) {
cur.right = new TreeNode(v);
cur = cur.right;
}
return ans.right;
}
public void inorder(TreeNode node, List<Integer> vals) {
if (node == null) return;
inorder(node.left, vals);
vals.add(node.val);
inorder(node.right, vals);
}
}
- 二叉搜索树的范围和
力扣
给定二叉搜索树的根结点 root,返回值位于范围 [low, high] 之间的所有结点的值的和
示例 1:
输入:root = [10,5,15,3,7,null,18], low = 7, high = 15
输出:32
示例 2:
输入:root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出:23
思路
public int rangeSumBST(TreeNode root, int low, int high) {
ArrayList<Integer> res = new ArrayList<>();
range(root,res);
int count =0;
for(int i :res){
if(i >= low && i<= high){
count += i;
}
}
return count;
}
public void range(TreeNode root,ArrayList<Integer> res){
if(root == null) return;
if(root.left != null){
range(root.left,res);
}
if(root.right != null){
range(root.right,res);
}
}
int ans;
public int rangeSumBST(TreeNode root, int low, int high) {
ans =0;
range(root,low,high);
return ans;
}
public void range(TreeNode root,int low, int high){
if(root != null){
if(root.val >= low && root.val <= high){
ans += root.val;
}
if(root.val > low){
range(root.left,low,high);
}
if(root.val < high){
range(root.right,low,high);
}
}
}
- 单值二叉树
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。只有给定的树是单值二叉树时,才返回 true;否则返回 false。
示例 1:
输入:[1,1,1,1,1,null,1]
输出:true
示例 2:
输入:[2,2,2,5,2]
输出:false
思路
public boolean isUnivalTree(TreeNode root) {
if(root == null) return false;
Set<Integer> set = new HashSet<>();
set.add(root.val);
if(root.left != null){
isUnivalTree(root.left);
}
if(root.right != null){
isUnivalTree(root.right);
}
if(!set.contains(root.val)){
return false;
}
return true;
}
public boolean isUnivalTree(TreeNode root) {
if(root == null) return false;
ArrayList<Integer> res = new ArrayList<>();
dfs(root,res);
for(int i :res){
if(i != res.get(0)){
return false;
}
}
return true;
}
public void dfs(TreeNode node,ArrayList<Integer> res){
if(node != null){
res.add(node.val);
dfs(node.left,res);
dfs(node.right,res);
}
}
- 二叉树的堂兄弟节点
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。如果二叉树的两个节点深度相同,但父节点不同,则它们是一对堂兄弟节点。我们给出了具有唯一值的二叉树的根节点 root,以及树中两个不同节点的值 x 和 y。只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true。否则,返回 false。
示例 1:
输入:root = [1,2,3,4], x = 4, y = 3
输出:false
示例 2:
输入:root = [1,2,3,null,4,null,5], x = 5, y = 4
输出:true
class Solution {
Map<Integer, Integer> depth;
Map<Integer, TreeNode> parent;
public boolean isCousins(TreeNode root, int x, int y) {
depth = new HashMap();
parent = new HashMap();
dfs(root, null);
return (depth.get(x) == depth.get(y) && parent.get(x) != parent.get(y));
}
public void dfs(TreeNode node, TreeNode par) {
if (node != null) {
depth.put(node.val, par != null ? 1 + depth.get(par.val) : 0);
parent.put(node.val, par);
dfs(node.left, node);
dfs(node.right, node);
}
}
}
Map<Integer, Integer> depth = new HashMap<>();
Map<Integer, TreeNode> parent = new HashMap<>();
public boolean isCousins(TreeNode root, int x, int y) {
if(root == null) return false;
dfs(root,null);
return depth.get(x) == depth.get(y) && parent.get(x) != parent.get(y);
}
public void dfs(TreeNode root,TreeNode par){
if(root != null){
depth.put(root.val ,par != null ? 1+depth.get(par.val) :0);
parent.put(root.val,par);
dfs(root.left,root);
dfs(root.right,root);
}
}
- 从根到叶的二进制数之和
给出一棵二叉树,其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。例如,如果路径为 0 -> 1 -> 1 -> 0 -> 1,那么它表示二进制数 01101,也就是 13 。对树上的每一片叶子,我们都要找出从根到该叶子的路径所表示的数字。返回这些数字之和。题目数据保证答案是一个 32 位 整数。
示例 1:
输入:root = [1,0,1,0,1,0,1]
输出:22
解释:(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
示例 2:
输入:root = [0]
输出:0
示例 3:
输入:root = [1]
输出:1
class Solution {
int ans;
public int sumRootToLeaf(TreeNode root) {
sumbinary(root, 0);
return ans;
}
public void sumbinary(TreeNode root, int cur){
if(root == null){
return;
}
if(root.left == null && root.right == null){
ans += cur * 2 + root.val;
return;
}
sumbinary(root.left, cur * 2 + root.val);
sumbinary(root.right, cur * 2 + root.val);
}
}
剑指 Offer 27. 二叉树的镜像
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
4
/ \
2 7
/ \ / \
1 3 6 9
镜像输出:
4
/ \
7 2
/ \ / \
9 6 3 1
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
思路
public TreeNode mirrorTree(TreeNode root) {
TreeNode res = new TreeNode();
if(root == null) return res;
if(root.left != null && root.right != null){
swap(root.left,root.right);
}
mirrorTree(root.left);
mirrorTree(root.right);
return res;
}
public void swap(TreeNode root1,TreeNode root2){
TreeNode tmp = new TreeNode(0);
tmp = root1;
root1= root2;
root2 = tmp;
}
public TreeNode mirrorTree(TreeNode root) {
if(root == null) return null;
TreeNode tem = root.left;
root.left = mirrorTree(root.right);
root.right = mirrorTree(tem);
return root;
}
剑指 Offer 28. 对称的二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
思路
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
if(root.left != null || root.right != null){
return false;
}
if(root.left != null && root.right != null){
return isequal(root.left,root.right);
}
isSymmetric(root.left);
isSymmetric(root.right);
return false;
}
public boolean isequal(TreeNode root1,TreeNode root2){
return root1.val == root2.val;
}
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return isequal(root.left,root.right);
}
public boolean isequal(TreeNode root1,TreeNode root2){
if(root1 == null && root2 == null) return true;
if(root1 == null || root2 == null || root1.val != root2.val) return false;
return isequal(root1.left,root2.right) && isequal(root1.right,root2.left);
}
剑指 Offer 32 - II. 从上到下打印二叉树 II
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
思路
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> queue = new List<List<>>();
ArrayList<TreeNode> cur = new ArrayList<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode node = root;
cur.add(root);
if(node.left != null){
cur.add(node.left);
}
if(node.right != null){
cur.add(node.right);
}
queue.offer(cur);
}
return queue;
}
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
if(root == null) return res;
queue.offer(root);
while(!queue.isEmpty()){
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size() ; i>0; i--){
TreeNode node = queue.poll();
tmp.add(node.val);
if(node.left != null){
queue.add(node.left);
}
if(node.right != null){
queue.add(node.right);
}
}
res.add(tmp);
}
return res;
}
剑指 Offer 54. 二叉搜索树的第k大节点
给定一棵二叉搜索树,请找出其中第k大的节点。
示例 1:
输入: root = [3,1,4,null,2], k = 1
3
/
1 4
2
输出: 4
示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
输出: 4
思路
List<Integer> res = new ArrayList<>();
public int kthLargest(TreeNode root, int k) {
int[] tmp = res.toArray();
return tmp[k];
}
public void dfs(TreeNode root,List<Integer> res){
if(root == null) return;
res.add(root.val);
dfs(root.left);
dfs(root.right);
}
int res;
int k;
public int kthLargest(TreeNode root, int k) {
this.k =k;
dfs(root);
return res;
}
public void dfs(TreeNode root){
if(root == null ) return;
dfs(root.right);
// if(k ==0) return;
if(--k ==0) res = root.val;
dfs(root.left);
}
剑指 Offer 55 - I. 二叉树的深度
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
public int maxDepth(TreeNode root) {
if(root == null) return 0;
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return Math.max(left+1,right+1);
}
剑指 Offer 55 - II. 平衡二叉树
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
返回 false 。
思路
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
if(Math.abs(depth(root.left) - depth(root.right)) <= 1){
return true;
}
return false;
}
public int depth(TreeNode root){
if(root == null ) return 0;
int left = depth(root.left);
int right = depth(root.right);
return Math.max(left+1,right+1);
}
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
if(Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right)){
return true;
}
return false;
}
public int depth(TreeNode root){
if(root == null ) return 0;
int left = depth(root.left);
int right = depth(root.right);
return Math.max(left+1,right+1);
}
剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
List<TreeNode> pathp = path(root,p);
List<TreeNode> pathq = path(root,q);
TreeNode cur = null;
for(int i = 0; i< pathp.size() && i<pathq.size(); i++){
if(pathp.get(i) == pathq.get(i)){
cur = pathp.get(i);
}
}
return cur;
}
public List<TreeNode> path(TreeNode root, TreeNode res){
List<TreeNode> list = new ArrayList<>();
TreeNode node = root;
while(node != res){
list.add(node);
if(res.val < node.val){
node =node.left;
}else {
node = node.right;
}
}
list.add(node);
return list;
}
剑指 Offer 68 - II. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
存储父节点
Map<Integer,TreeNode> parent = new HashMap<>();
Set<Integer> res = new HashSet<>();
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
dfs(root);
while(p != null){
res.add(p.val);
p = parent.get(p.val);
}
while(q != null){
if(res.contains(q.val)){
return q;
}
q = parent.get(q.val);
}
return null;
}
public void dfs(TreeNode root){
if(root.left != null){
parent.put(root.left.val,root);
dfs(root.left);
}
if(root.right != null){
parent.put(root.right.val,root);
dfs(root.right);
}
}
面试题 04.02. 最小高度树
给定一个有序整数数组,元素各不相同且按升序排列,编写一个算法,创建一棵高度最小的二叉搜索树。
示例:
给定有序数组: [-10,-3,0,5,9],
一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树:
0
/ \
-3 9
/ /
-10 5
public TreeNode sortedArrayToBST(int[] nums) {
if(nums.length ==0) return null;
return createtree(nums,0,nums.length-1);
}
public TreeNode createtree(int[] nums,int left,int right){
if(left < 0 || left > right || right >= nums.length) return null;
int mid = (left + right)/2;
TreeNode root = new TreeNode(nums[mid]);
root.left = createtree(nums,left,mid-1);
root.right = createtree(nums,mid+1,right);
return root;
}
面试题 17.12 BiNode
二叉树数据结构TreeNode可用来表示单向链表(其中left置空,right为下一个链表节点)。实现一个方法,把二叉搜索树转换为单向链表,要求依然符合二叉搜索树的性质,转换操作应是原址的,也就是在原始的二叉搜索树上直接修改。
返回转换后的单向链表的头节点。
注意:本题相对原题稍作改动
示例:
输入: [4,2,5,1,3,null,6,0]
输出: [0,null,1,null,2,null,3,null,4,null,5,null,6]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
TreeNode cur = new TreeNode(-1);
TreeNode pre = null;
public TreeNode convertBiNode(TreeNode root) {
helper(root);
return cur.right;
}
public void helper(TreeNode root){
if(root == null) return;
helper(root.left);
if(pre == null){
pre = root;
cur.right = root;
}else{
pre.right = root;
pre = root;
}
root.left = null;
helper(root.right);
}