遗传算法原理及其在车辆路径规划中的应用

1.遗传算法的原理

        遗传算法（GA）是一种启发式搜索算法。遗传算法基于自然选择和遗传学的思想. 遗传算法模拟自然选择的过程，即那些能够适应环境变化的物种能够生存和繁殖并进入下一代。简单地说，遗传算法模拟连续一代个体之间的“适者生存”来解决问题。每一代由一群个体组成，每个个体代表搜索空间中的一个点和可能的解决方案。每个个体可表示为字符串/整数/浮点数等,类似于染色体.

2.遗传算法基本概念

        遗传算法是基于种群染色体的遗传结构和行为。以下是遗传算法的基础概念.

         1.每条染色体(Chromosome)表示一个可能的解决方案;每条染色体由基因组成(Gene);种群(Population)是染色体的集合.

 

        2.适应度函数用于衡量每条染色体的优劣.适应度更高的个体表明该方案更优秀,有更大的概率"遗传"给下一代.

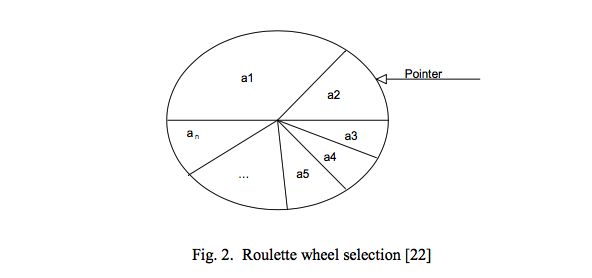
        3.选择.利用适应度函数计算出种群中每个个体的适应度后,优胜劣汰,从中挑选出优良个体组成新的种群.常见选择策略有轮盘赌(Roulette Wheel Selection),锦标赛选择(Tournament Selection)等.

        3.1轮盘赌

        个体被选择的概率与其适应度正相关,适应度越高的个体,被选择的概率更高.公式为    

                        ​​​​                          

        个体的选择概率累加,即为为累加概率,直观理解,相当于上图轮盘各个个体对应的刻度(区域).公式为

                        ​​​​​​​        ​​​​​​​                        

        看到这里,有些读者可能会有疑问(没有的话聪明的你可以跳过进入下一节),如上图公式,累积概率还与个体的顺序有关,例如有四个个体,其对应的选择概率Pselect为[0.4,0.3,0.2,0.1],那么其累积概率则为[0.4,0.7,0.9,1],可知第四个个体的累积概率为1,那么每次选择难道不会都选择该个体吗?其实不会的,可以将其理解成分段函数,分别为[0,0.4],[0.4,0.7],[07,0.9],[0.9,1].对于一个随机概率,其落在这四段上的概率只与各段的长度相关,与其顺序无关.

        3.2锦标赛选择

        锦标赛选择是遗传算法中流行的选择策略,简单高效.所谓的锦标赛选择,就是从种群中随机选择若干个个体,在这些个体中比较其适应度,选择出适应度大的个体.

                ​​​​​​​

        以3元锦标赛选择为例,如上图所示,从种群中随机选择3个个体,A,E,T.比较其适应度得分,最后选择出最优个体A.

4.交叉(Crossover)

        交叉类似于生物的繁殖,利用"父母"的遗传特征,产生一个或多个后代。通常设置一个较大的交叉概率,在每轮"繁衍"的过程中,同时生成一个随机概率,若该概率小于交叉概率,则进行交叉操作,反之则直接接受父母的基因,不进行交叉.

        常见的交叉操作有单点交叉,多点交叉等.

        单点交叉，随机选择一个交叉点，交换交叉点后父母的基因以获得新的后代。

        多点交叉,是单点交叉的推广，交叉点之间的基因段被交换以获得新的子代。

5.变异(Mutation)

        在自然界中,少数新生的后代中，它们的一些基因可能会发生小概率的突变,导致出现与"父母"不同的性状。突变恰好照顾了种群之间的多样性并阻止了过早的收敛。

        在实际的操作中,通常会设置一个较小的变异概率,如果变异概率很大，整个搜索过程就退化为一个随机搜索过程。所以，比较稳妥的做法是，进化过程刚刚开始的时候，取p为一个比较大的概率，随着搜索过程的进行，p逐渐缩小到0附近.

3. 遗传算法的基本流程

        上面介绍了遗传算法的基本概念,下面以流程图的形式串起整个流程.

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                ​​​​​​​

 

        在解决实际问题时,首先需要将问题抽象映射成可以以数字表示的形式.所谓的初始化,类似于编码,

        算法程序是不能处理非数字形式的类型.例如笔者在进行车辆路径优化(Vehicle Routing Problems with Time Windows)算法开发时,首先需要将客户实际地址映射成这样[1,2,...] 由数字组成的address列表.其中每一个数字代表一个地址.在自然界中,动物种群的规模是一定的,所以在遗传算法中,种群的规模也是受限的.种群规模太小缺乏多样性,可行解的搜索空间小,生成的解的质量不高,种群规模过大会导致求解速度慢.

        在实际操作中,随机打乱address列表,重复n次,这样就完成了初始化,生成了包含n个个体的种群.

        对于遗传算法而言,每个个体代表一个解决方案.在初始化种群后,需要计算每个解决方案的适应度得分.

        接上面的例子,在车辆调度任务,一般的优化目标为车辆行驶的总距离为

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                        ​​​​​​​

        其中,i表示某条线路,n表示线路条数.distance_i 代表某条线路的距离.在一些例子中,这个距离是欧式距离.在实际生产中,通过一些地图api接口返回实际的行驶距离更具有可用性.

        对于需要同时优化距离和运输车辆数量,可以设置一个固定的车辆成本系数C1,距离的惩罚系数C0,此时适应度函数优化目标为

        ​​​​​​​        ​​​​​​​                        

        其中,Vehicles 表示实际使用的车辆数量,与线路条数的含义相同.

        在计算完每个个体的适应度得分后.进行个体的选择.二元锦标赛选择(Binary Tournament Selection)是最常用的方法.

        锦标赛选择的原理上文已经解释过,这里就一笔带过,每次随机选择两个个体(以二元锦标赛为例),比较其适应度得分,选择适应度高的个体,重复N次.选择出N个个体.

        在选择出合适的个体后,下一步开始进行交叉操作.随机从种群中选择两个个体作为父本和母本,随机选择多个位置点进行基因的交换.原理不再赘述.在车辆路径优化中,个体或者说染色体是由运输点编码构成的,所以需要注意交叉后的染色体不可出现重复的数字,即同一个地点不可出现两次.

        对于变异操作,在车辆调度中,由于每个基因代表一个实际的运输点,所以变异后的基因不可凭空或者重复出现,一个简单的方法是随机交换个体中某几个点的基因.

至此,遗传算法的整个流程就结束了,重复多次,直到达到算法停止条件,完成算法的求解.

4.总结

        与传统方法相比，遗传算法速度更快，效率更高,能够优化连续和离散及多目标问题,并且总能得到问题的解.

不过GA并不适合所有问题，适应度值是重复计算的，所以对于某些问题，计算成本可能很高。 遗传算法在求解中过程中有很大的随机性，不能保证解决方案的最优性或质量,可能无法收敛到最佳解决方案.

        从笔者的实际经验而言,在车辆路径规划问题中,遗传算法求解出的可行解质量相比于一些领域搜索算法而言,相对较差.