数据结构——二叉树篇(二叉搜索树、平衡二叉树、堆、哈夫曼树)
数据结构——二叉树
- 数据结构——二叉树篇
- 1.最基本的二叉树
-
- 基本介绍
-
- 描述
- 概念
- 小贴士
- 代码实现
- 2.二叉搜索树
-
- 基本介绍
-
- 描述
- 概念
- 小贴士
- 代码实现
- 2.平衡二叉树(AVL树)
-
- 基本介绍
-
- 描述
- 概念
- 小贴士
- 代码实现
- 3.堆
-
- 基本介绍
-
- 描述
- 概念
- 小贴士
- 代码实现
- 4.哈夫曼树
-
- 基本介绍
-
- 描述
- 概念
- 小贴士
- 代码实现
数据结构——二叉树篇
1.最基本的二叉树
基本介绍
描述
一个二叉树是一个有穷的结点集合,这个集合可以为空(称其为空树),若不为空,则它是由根结点和称为该根节点的左子树和右子树两个不相交的二叉树组成。任何一棵n叉树/一个n叉树森林都可以使用“左孩子,右兄弟”法转化为一棵二叉树,当然,把一棵二叉树转化为一棵n叉树/一个n叉树森林,必须要事先声明转化的目标是一棵n叉树还是一个n叉树森林
概念
度:
节点的度——每一个节点的子节点个数
树的度——树的所有节点中最大的节点的度
节点:
祖先节点——沿树根到某一个节点路径上的所有节点(也包括根节点)都是这个节点的祖先节点
子孙节点——某一个节点的子树中的所有节点都是这个节点的子孙节点
叶子节点——既没有左子节点又没有右子节点的树节点
深度:
节点的深度——规定根节点在第一层,其他任一节点所在层数为其父节点所在层数+1
树的深度——树的所有节点中最大的节点的层次
高度:
类比于根节点在第一层,叶节点的高度规定为1
值得一提的是,同一棵树的高度和深度相同
分支:
指节点和节点之间的连线
路径长度:
为该路径所包含的分支的个数
先序遍历
从一棵树的根结点开始,对于每一个结点,都是先访问本结点,再访问左子结点,最后访问右子结点,实现对树中的每一个结点进行不重复,不遗漏的访问
中序遍历
从一棵树的根结点开始,对于每一个结点,都是先访问左子结点,再访问本结点,最后访问右子结点,实现对树中的每一个结点进行不重复,不遗漏的访问
后序遍历
从一棵树的根结点开始,对于每一个结点,都是先访问左子结点,再访问右子结点,最后访问本结点,实现对树中的每一个结点进行不重复,不遗漏的访问
层序遍历
从一棵树的根结点开始,按照从上至下,从左至右的顺序,实现对树中的每一个结点进行不重复,不遗漏的访问
小贴士
树的三种经典遍历的过程?
前序遍历的输出顺序:根值 左子值 右子值
中序遍历的输出顺序:左子值 根值 右子值
后序遍历的输出顺序:左子值 右子值 根值
二叉树的分类?
斜二叉树/退化二叉树:
所有的结点都只有左子树或者都只有右子树,此时树的结构已经退化为线性表
完全二叉树:
对树中结点按从上至下,从左至右的顺序进行编号,每一个结点的编号和完美二叉树的对应位置的结点的编号完全一致。完全二叉树常使用顺序存储的形式进行数据存储
完美二叉树/满二叉树:
在第一个结点的编号从1开始计算的条件下,如果一个节点的编号为i,则其左孩子编号为2i,其右孩子编号为2i+1。所有的节点都存在左子树和右子树,并且所有的叶节点都在同一层上。完美二叉树/满二叉树常使用顺序存储的形式进行数据存储
先序遍历、中序遍历、后序遍历时将叶子结点进行打印,结果是否相同?
是相同的,因为三种遍历对于每一个结点,都是先去左子结点再去右子结点,所以三种遍历经过各个树结点的路径是完全相同的,即经过各个叶子结点的顺序是完全相同的,故打印结果完全一致
题外话:为什么进行三种遍历的时候,打印各个树结点的顺序不同呢?
因为遍历的过程中,有三次机会经过同一个结点,分别是
1.从该结点的父节点,进入这个结点;
2.从该结点的左子节点,进入这个结点;
3.从该结点的右子节点,进入这个结点;
打印每一个结点的时候,在不同的时候进行打印,自然结果各不相同
不要把路径和输出结果混为一谈。对于同一棵树,三种遍历方式的路径完全相同,一般遍历结果就是指输出结果
二叉树中的数学公式?
在树型结构中,会有很多等式,熟练记忆一些等式可以带来很多便利
(1)一棵二叉树的第 i 层最多可以有 2i-1 个树结点
(2)深度为 i 的二叉树的最多可以有 2i-1 个树结点
(3)对于一个非空二叉树,都有 叶子结点的个数 = 度为2的结点的个数 + 1
(4)一个具有n个结点的完全二叉树的深度为
⌊ log 2 n ⌋ + 1 ⌊ \log\nolimits_2n⌋+1 ⌊log2n⌋+1
代码实现
结构定义
typedef struct TNode //树的结点的结构定义
{
int data;
struct TNode* Left;
struct TNode* Right;
}*PtrToTNode;
typedef PtrToTNode Tree;
1.树的高度/深度的三种求法
(1)递归法求深度
int depth = 0; //depth为一个全局变量,用来记录当前的树的深度
void get_Depth(Tree t, int d) //d初始传入1
{
if (t != NULL)
{
if (d > depth) depth = d; //注意,一定要判断当d > depth时,进行赋值,因为根据递归方式,
//是先不断递归进入结点的左子树,不断累加depth,等到左子树为空时,才会开始进入右子树,
//此时可能会出现depth的值大于d情况,如果不做判断,进行赋值,会导致高度计算出错
get_Depth(t->Left, d + 1); //d+1为下一层的结点的深度,已经帮下一次结点计算好了
get_Depth(t->Right, d + 1);
}
}
(2)递归法求高度
int get_Height(Tree t)
{
if (t != NULL)
{
int LH = get_Height(t->Left);
int RH = get_Height(t->Right);
int H = LH > RH ? LH : RH; //取两个子树的较高的树高
return H + 1; //+1是为了计算本结点的高度
}
else
return 0;
}
(3)层序遍历求高度
int Level_Depth(Tree t)
{
if (t == NULL) return 0;
Tree q[100];
int Front, Rear;
int LastPoint = 0; //LastPoint存储的是每一层的最后一个结点的下标,初始化为0的操作是关键性的
int Level = 0;
Tree p = NULL;
Front = Rear = -1;
Rear++;
q[Rear] = t;
while (Front < Rear) //当Front == Rear的时候,队列中无元素,结束遍历
{
Front++;
p = q[Front]; //进行结点的出队操作
if (p->Left != NULL)
{
Rear++;
q[Rear] = p->Left; //当左子结点存在的时候,进行左子结点的入队操作
}
if (p->Right != NULL)
{
Rear++;
q[Rear] = p->Right; //当右子结点存在的时候,进行右子结点的入队操作
}
if (Front == LastPoint) //当一层的所有结点都出队的时候(这个时候下一层所有的结点也全部入队完成了)
{ //记录的层数+1,并将LastPoint置于下一层的最后一个结点处
Level++;
LastPoint = Rear;
}
}
return Level;
}
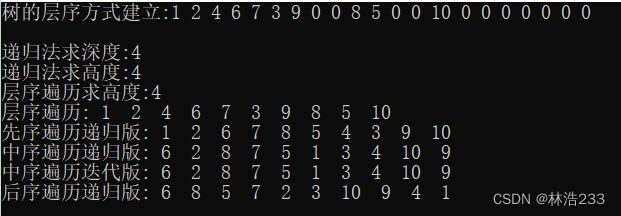
2.树的层序方式建立
Tree CreateBinTree()
{
Queue q = Init_Queue(1000); //队列的存在是为了保证数据的输入是按照层序进行赋值的
int data; //存储每一次输入的数据
Tree t = NULL;
PtrToTNode n;
scanf("%d", &data);
if (data == 0) //判断第一次输入的数据是否为无效数据,
//是,直接返回NULL,否,进行树的创建
return NULL;
else
{
t = Init_TNode(data);
QPush(q, t);
}
while (!qIsEmpty(q)) //直到队列为空,即所有的节点都出队为止,循环结束,停止数据输入
{
n = QPop(q);
scanf("%d", &data);
if (data == 0)
n->Left = NULL;
else
{
n->Left = Init_TNode(data); //每构造好一个节点,就将其入队,
QPush(q, n->Left); //每一次节点的出队,都会进行输入
} //数据的判断,看是否要进行该出队节点的子节点的构造
scanf("%d", &data);
if (data == 0)
n->Right = NULL;
else
{
n->Right = Init_TNode(data);
QPush(q, n->Right);
}
}
return t;
}
3.树的遍历
[1]层序遍历
普通版
只会层序打印出非NULL的节点数值
void LevelTravelsal(Tree t)
{
PtrToTNode n;
Queue q = Init_Queue(1000);//队列的存在是为了保证数据的输出是按照层序进行输出的
if (t == NULL)
printf("此为空树,无法输出");
else
QPush(q, t);
while (!QIsEmpty(q))
{
n = QPop(q);
printf(" %d ", n->data);
if (n->Left) QPush(q, n->Left); //每一个节点的出队,都会进行其数据的输出,并
if (n->Right) QPush(q, n->Right); //判断其是否具有子节点,判断是否要将子节点入队
}
}
测试版
可以打印出NULL的节点数值(以0代替),便于读者直接画出二叉树,从而进行二叉树代码检验
void LevelTravelsal_Test(Tree t)
{
PtrToTNode n;
Queue q = Init_Queue(1000);
if (t == NULL)
printf("此为空树,无法输出");
else
QPush(q, t);
while (!QIsEmpty(q))
{
n = QPop(q);
if (n != NULL)
printf(" %d ", n->data);
else
printf(" 0 "); //对于NULL的树节点,打印的数值为0
if (n != NULL)
{
QPush(q, n->Left);
QPush(q, n->Right);
}
}
}
与层序遍历配套的队列代码
typedef struct QNode //队列的定义
{
PtrToTNode* data;
int Front, Rear;
int max;
int size;
}*Queue;
Queue Init_Queue(int max) //循环顺序队列的初始化(使用的是size方法)
{
Queue q = (Queue)malloc(sizeof(struct QNode));
q->data = (PtrToTNode*)malloc(max * sizeof(PtrToTNode));
q->Front = q->Rear = 0;
q->size = 0;
q->max = max;
return q;
}
bool QIsEmpty(Queue q) //循环顺序队列的判空
{
return q->size == 0;
}
bool QIsFull(Queue q) //循环顺序队列的判满
{
return q->size == q->max;
}
bool QPush(Queue q, PtrToTNode val) //循环顺序队列的元素入队
{
if (QIsFull(q)) return false;
q->Rear = (q->Rear + 1) % q->max;
q->data[q->Rear] = val;
q->size++;
return true;
}
PtrToTNode QPop(Queue q) //循环顺序队列的队首元素出队
{
if (QIsEmpty(q)) return (PtrToTNode)ERROR;
PtrToTNode data;
q->Front = (q->Front + 1) % q->max;
data = q->data[q->Front];
q->size--;
return data;
}
[2]先序遍历
递归版
void PreorderTravelsal(Tree t)
{
if (t)
{
printf(" %d ", t->data);
PreorderTravelsal(t->Left);
PreorderTravelsal(t->Right);
}
}
[3]中序遍历
(1)递归版
void InorderTravelsal_1(Tree t)
{
if (t)
{
InorderTravelsal_1(t->Left);
printf(" %d ", t->data);
InorderTravelsal_1(t->Right);
}
}
(2)迭代版
void InorderTravelsal_2(Tree t)//很像写已知树的中序遍历的过程
{
PtrToTNode n = NULL;
Stack s = Init_Stack();
while (s->next != NULL || t)
{
while (t) //当节点没有左节点的时候跳出while循环,进行该无右节点的节点的数据输出
{
SPush(s, t);
t = t->Left;//后入栈左节点,先输出左节点
//根节点都是比左节点先入栈,后输出
}
n = SPop(s);
printf(" %d ", n->data);
t = n->Right; //等到左节点和根节点都出栈了(输出)以后,右节点开始入栈
}
}
[4]后序遍历
递归版
void PostorderTravelsal(Tree t)
{
if (t)
{
PostorderTravelsal(t->Left);
PostorderTravelsal(t->Right);
printf(" %d ", t->data);
}
}
4.树的删除
void Delete_Tree(Tree t)
{
if (t != NULL)
{
Delete_Tree(t -> Left);
Delete_Tree(t -> Right);
free(t);
}
}
主函数测试
使用上述全部函数,添加了堆栈和队列的代码(更多代码详见数据结构——线性结构篇),并进行了相应的修改,下面的代码读者可以整个复制下来,平时可以练习写出几种遍历方式的序列,与运行结果进行核对
#include2.二叉搜索树
基本介绍
描述
二叉搜索树又称二叉排序树或者二叉查找树,是一种对排序和查找都很有用的特殊二叉树,为了方便起见,规定各个结点的数据都不相同
一棵二叉搜索树应该满足以下条件:
1.非空左子树的所有键值都小于其根节点的键值
2.非空右子树的所有键值都大于其根节点的键值
3.左右子树都是二叉搜索树
概念
平均查找长度(ASL):
查找各个结点所花费的访问次数之和,再取一个平均值得到的结果
在搜索树中具体来说就是每一层的结点数乘以该层结点的树的深度(即成功查找该结点的数据需要的比较次数)之后,求和,再除以结点总数得到的结果
小贴士
二叉搜索树的删除数据操作的解析?
二叉搜索树的删除数据操作是一个递归算法
二叉搜索树要删除的目标结点有三种情况:
1.完全没有子节点(即目标结点为一个叶子结点)
直接对该结点进行删除即可,向其父结点返回一个NULL指针
2.只有一个子节点
也比较简单,直接对该结点进行删除,并向其父结点返回一个那个为唯一的子节点的地址
1.儿女双全(即左右子结点皆存在)
这种情况需要进行一个转化,转化为第二种情况去进行处理
首先,这个结点不是真正地进行删除,而是进行了一个数据的覆盖,具体来说,就是把其左(右)子树中的最大(小)数据赋值给该结点,然后转换删除目标,去删除那个左(右)子树中的最大(小)数据对应的结点
其次,这个替罪羊结点必定只有一个子节点(只有右节点或者左节点),因为如果该结点具有左节点,那该结点必定不是最小的那个数据对应的结点;如果该结点具有右节点,那该结点必定不是最大的那个数据对应的结点
所以这种操作进行了一个删除目标转化的操作,可以成功将第三种情况转化为第二种情况进行解决
这么操作的原因:
因为要保证删除目标数据以后的树,依旧符合二叉搜索树的定义,即依旧符合那三个条件,所以是将左子树中的最大数据赋值给该结点,或者将右子树中的最小数据赋值给该结点,因为两种方法进行删除,转化第三种情况为第二种情况,删除数据完毕以后,这颗树一定都是符合二叉搜索树的定义的
对于同一组数据,不同的插入方式会导致建立的二叉树不一样?
对的,所以对于普通二叉搜索树的数据插入顺序要进行一定的考虑
因为按照二叉搜索树的插入方式,每一次插入一个数据,都是经过多次比较,得到该数据的合适位置,期间,对于已经存在的数据的位置是不会进行变动的。也正是因为不会进行变动,就会导致对于同一组数据,如果用户插入数据的顺序不适当,就会使查找效率大大减低(极端的情况就是变成一棵退化二叉树),为了解决这个问题,我们研究出了会自动进行已有数据位置调整的平衡二叉树
二叉搜索树的最小数据和最大数据位置的确定?
根据二叉树搜索树的定义,
最小数据位置的寻找:从根结点开始,不断向结点的左子树移动,直到无路可走为止
最大数据位置的寻找:从根结点开始,不断向结点的右子树移动,直到无路可走为止
所以若一搜索树(查找树)是一个有n个结点的完全二叉树,则该树的最大值不一定在叶结点上
若一搜索树(查找树)是一个有n个结点的完全二叉树,则该树的最小值一定在叶结点上
代码实现
1.动态查找
(1)递归版
PtrToTNode Find(Tree t, int val)
{
if (t == NULL) //如果树为空,返回空,表示查找不到该数据
return NULL;
else
{
if (val > t->data)
return Find(t->Right, val);
else if (val < t->data)
return Find(t->Left, val);
else //if (val == t->data)
return t;
}
}
(2)迭代版
PtrToTNode Find(Tree t, int val)
{
if (t == NULL) //如果传入的树为空,返回空,表示传入的树为空,无法进行查找
return NULL;
else
{
while (t)
{
if (val > t->data)
t = t->Right;
else if (val < t->data)
t = t->Left;
else
return t;
}
}
return NULL; //如果传入的树为非空,查找不到该数据,返回空,表示查找不到该数据
}
2.查找最大值
(1)递归版
PtrToTNode FindMax(Tree t)
{
if (t == NULL)
return NULL; //如果传入的树为空,返回空,表示无法进行查找,根本没有任何数据
else if (t->Right != NULL)
return FindMax(t->Right); //如果传入的节点地址的下标非零,根据二叉搜索树的定义,该节点并不是存储最大值的节点,递归继续寻找
else //(t->Right == NULL)
return t; //如果传入的节点地址的下标为零,根据二叉搜索树的定义,该节点即为存储最大值的节点,返回该节点的地址
}
(2)迭代版
PtrToTNode FindMax(Tree t)
{
if (t == NULL)
return NULL; //如果传入的树为空,返回空,表示无法进行查找,根本没有任何数据
else
{
while (t->Right != NULL) //当节点的右节点为空时,跳出循环,接着返回该节点的地址
t = t->Right;
return t;
}
}
3.查找最小值
(1)递归版
PtrToTNode FindMin(Tree t)
{
if (t == NULL)
return NULL;
else if (t->Left != NULL)
return FindMin(t->Left);
else
return t;
}
(2)迭代版
PtrToTNode FindMin(Tree t)
{
if (t == NULL)
return NULL;
else
{
while (t->Left != NULL)
t = t->Left;
return t;
}
}
4.数据的插入
Tree Insert(Tree t, int val)
{
if (t == NULL)
{
t = Init_TNode(val); //如果传入的节点地址为零,创建一个新的节点,并返回其地址
return t;
}
else //如果传入的节点地址不为零,下面的代码会不断进行递归直到找到合适的叶子节点,
//使下一次递归调用时,传入节点地址为空,从而实现新数据的插入
{
if (val > t->data)
t->Right = Insert(t->Right, val);
else if (val < t->data)
t->Left = Insert(t->Left, val);
//if (val == t->data) 不进行任何操作
return t;
}
}
5.数据的删除
Tree Delete(Tree t, int val)
{
PtrToTNode n = NULL;
//【第一层判断】,判断该树节点是否为空
if (t == NULL)
{
printf("找不到对应元素,无法进行删除\n");
return NULL;
}
else
{ //【第二层判断】,判断目标树节点的位置
if (val > t->data)
{
t->Right = Delete(t->Right, val);
return t;
}
else if (val < t->data)
{
t->Left = Delete(t->Left, val);
return t;
}
else//前两个选择结构进行了一个方向的不断调整,如果到达该代码处
//(即前两个条件均不符合),说明该节点即为目标节点(要被删除的节点)
{
//【第三层判断】,现已找到了目标节点,判断该目标节点是三种树节点类型的哪一种
if (t->Right != NULL && t->Left != NULL)//如果要被删除的节点儿女双全,则进行数据的覆盖(一种隐形的删除方法),
//并把要删除数据目标转移到左子树的最大数据 或者 右子树的最小数据上
{
t->data = FindMax(t->Left)->data;
t->Left = Delete(t->Left, t->data);
return t;
}
else if (t->Left != NULL) //如果该要被删除的节点只有左子节点,则把左子节点进行返回,并释放该节点空间
{
n = t->Left;
free(t);
return n;
}
else
//如果该要被删除的节点只有右子节点 或者 无子节点,则把右子节点进行返回
//(没有的时候,返回NULL,也符合我们的预期目标),并释放该节点空间
{
n = t->Right;
free(t);
return n;
}
}
}
}
主函数测试
#define maxop 20
int main()
{
srand((unsigned)time(NULL));
int val, op, i = 0;
Tree t = NULL;
for (i; i < maxop; i++)
{
val = rand() % 100;
op = rand() % 4;
switch (op)
{
case 0: {
printf("插入元素 %d \n", val);
t = Insert(t, val);
break;
}
case 1: {
printf("删除元素 %d \n", val);
Delete(t, val);
break;
}
case 2: {
printf("插入元素 %d \n", val);
t = Insert(t, val);
break;
}
case 3: {
printf("插入元素 %d \n", val);
t = Insert(t, val);
break;
}
}
printf("前序遍历:");
PreorderTravelsal(t);
printf("\n");
printf("中序遍历:");
InorderTravelsal(t);
printf("\n");
printf("后序遍历:");
PostorderTravelsal(t);
printf("\n");
printf("层序遍历:");
LevelTravelsal_Test(t);
printf("\n");
printf("\n");
}
return 0;
}
2.平衡二叉树(AVL树)
基本介绍
描述
平衡二叉树为普通二叉搜索树的升级版(除了插入的操作的代码有较大改动以外,其他操作和普通的二叉搜索树基本一致),由于考虑到普通二叉搜索树最坏的时间复杂度可以达到和线性表的时间复杂度相同的地步(即二叉搜索树为一棵斜二叉树的情况),同时结合了二分查找的思想,于是研究出了可以自行对数据位置进行合理化调整的平衡二叉树。通过二叉平衡树,可以实现二叉搜索树查找数据的时间复杂度的稳定化,即将时间复杂度稳定为有序表的折半查找的时间复杂度
一棵平衡二叉树应该满足以下条件:
1.根节点的左右子树的高度差值不超过1
2.任一节点的左右子树皆为一棵AVL树
概念
导致问题节点:
即由于该树节点的插入,导致了不平衡现象的出现
发现问题节点:
即由于导致问题节点的插入,发现问题节点的平衡因子不处于一个合理范围内
平衡因子:
就是上面的"左右子树的高度差值"这几个字的高端说法
具体为左子树的高度减去右子树的高度所得到的一个数值
左左不平衡:
导致问题结点在发现问题结点左子结点的左子树中
右右不平衡:
导致问题结点在发现问题结点右子结点的右子树中
左右不平衡:
导致问题结点在发现问题结点左子结点的右子树中
右左不平衡:
导致问题结点在发现问题结点右子结点的左子树中
左单旋:
为了解决"左左不平衡"问题
调整过程涉及两个节点
过程是把发现问题结点的左子节点B变成发现问题结点A的父节点,同时发现问题结点A变成发现问题结点的左子节点B的右子结点
注意,在进行左单旋的时候,要将发现问题结点的左子节点B的右子树变成发现问题结点A的左子树
右单旋:
为了解决"右右不平衡"问题
调整过程涉及两个节点
过程是把发现问题结点的右子结点B变成发现问题结点A的父节点,同时发现问题结点A 变成发现问题结点的右子节点B的左子结点
注意,在进行右单旋的时候,要将发现问题结点的右子节点B的左子树变成发现问题结点A的右子树
左右双旋:
为了解决"左右不平衡"问题
调整过程涉及三个节点
过程是先针对发现问题结点的左结点B进行了一个右单旋,后面再对发现问题结点A进行了一个左单旋
右左双旋:
为了解决"右左不平衡"问题
调整过程涉及三个节点
过程是先针对发现问题结点的右结点B进行了一个左单旋,后面再对发现问题结点A进行了一个右单旋
小贴士
平衡二叉树的插入数据操作的解析?
是对普通二叉搜索树的插入数据操作的升级,是平衡二叉树之所以"平衡"的关键操作,在普通二叉搜索树的插入数据操作的基础上,添加了两段代码:
1.每一次插入之后,都会进行平衡因子的计算,如果计算出的平衡因子不在规定范围内,即会进行自动调整,使得每一个树结点的平衡因子都处在规定范围内,这个调整过程,需要对不平衡的情况(左左不平衡/右右不平衡/左右不平衡/右左不平衡)进行判定,然后对症下药,挑选对应的解决方法(左单旋/右单旋/左右双旋/右左双旋)
2.在插入数据以后,位于上层的每一个结点和本结点都要重新计算自身结点的树高
代码实现
结构定义
typedef struct AVLNode
{
int data;
int Height;
struct AVLNode* Left;
struct AVLNode* Right;
}*AVLNode;
typedef AVLNode AVLTree;
1.平衡树结点初始化
AVLNode Init_AVLNode(int val) //用来初始化平衡树的结点
{
AVLNode n = (AVLNode)malloc(sizeof(struct AVLNode));
n->data = val;
n->Height = 1; //树高度大于等于1(树的深度也是如此),每一个结点记录的都是以自身为根结点的树的高度
n->Left = n->Right = NULL;
return n;
}
2.求较大值的一个小函数
int Max(a, b)
{
return (a > b) ? a : b;
}
3.递归求树高
int getHeight(AVLTree t)
{
int Left_Height;
int Right_Height;
if (t == NULL)
return 0;
else
{
Left_Height = getHeight(t->Left); //此处皆为子树的高度(即以子节点为根结点的树的高度)
Right_Height = getHeight(t->Right);
return Max(Left_Height, Right_Height) + 1;
}
}
4.数据位置调整
(1)右单旋代码(用来处理"右右不平衡"导致的问题)
AVLTree SingleRightRotation(AVLTree t) //t为发现问题的结点
{
AVLNode n = t->Right; //n为t的右子结点
t->Right = n->Left; //先将t的右子结点的左子树变成t的右子树
n->Left = t; //再将t变成t的右子结点的左子结点
n->Left->Height = Max(getHeight(n->Left->Left), getHeight(n->Left->Right)) + 1; //更新一下树高
n->Height = Max(n->Left->Height, getHeight(n->Right)) + 1;
return n;
}
(2)左单旋代码(用来处理"左左不平衡"导致的问题)
AVLTree SingleLeftRotation(AVLTree t) //t为发现问题的结点
{
AVLNode n = t->Left; //n为t的左子结点
t->Left = n->Right; //先将t的左子结点的右子树变成t的左子树
n->Right = t; //再将t变成t的左子结点的右子树
n->Right->Height = Max(getHeight(n->Right->Right), getHeight(n->Right->Left)) + 1; //更新一下树高
n->Height = Max(getHeight(n->Left), n->Right->Height) + 1;
return n;
}
(3)右左双旋代码(用来处理"右左不平衡"导致的问题)
AVLTree DoubleRightLeftRotation(AVLTree t) //t为发现问题的结点
{
t->Right = SingleLeftRotation(t->Right); //先针对t的右子结点进行一个左单旋
t = SingleRightRotation(t); //再针对t进行一个右单旋
return t;
}
(4)左右双旋代码(用来处理"左右不平衡"导致的问题)
AVLTree DoubleLeftRightRotation(AVLTree t) //t为发现问题的结点
{
t->Left = SingleRightRotation(t->Left); //先针对t的左子结点进行一个右单旋
t = SingleLeftRotation(t); //再针对t进行一个左单旋
return t;
}
5.数据的插入
AVLNode Insert(AVLTree t, int val)
{
if (t == NULL)
t = Init_AVLNode(val);
else if (val < t->data)
{
t->Left = Insert(t->Left, val);
//以下为平衡树保持平衡(即平衡因子处于正常范围内)的关键代码
if (getHeight(t->Left) - getHeight(t->Right) == 2) //计算该结点的平衡因子,如果有可能导致不平衡,必定为该发现问题的结点(即t指针指向的结点)
//的左子树的高度"远"大于右子树的高度而造成的
//必须使用函数来求树的高度,因为t的左右指针可能为NULL
{
//到达此处,代表已经不平衡了,此时要进一步进行判断,为"左左不平衡"还是"左右不平衡"
if (val > t->Left->data) //表示为"左右不平衡"
{
t = DoubleLeftRightRotation(t); //注意,是将问题结点的指针传入,这是由函数代码的具体实现决定的
printf("【注意】插入过程中出现了左右不平衡\n");
}
else //表示为"左左不平衡"
{
t = SingleLeftRotation(t);
printf("【注意】插入过程中出现了左左不平衡\n");
}
//必定不会出现val == t->Left->data的情况,因为根据反证法,如果出现,表示此数据不会被插入,但是又因为这种情况而引发了不平衡,这是自相矛盾
}
}
else if (val > t->data)
{
t->Right = Insert(t->Right, val);
//以下为平衡树保持平衡(即平衡因子处于正常范围内)的关键代码(思路与上类似,不再赘述)
if (getHeight(t->Left) - getHeight(t->Right) == -2)
{
if (val < t->Right->data)
{
t = DoubleRightLeftRotation(t);
printf("【注意】插入过程中出现了右左不平衡\n");
}
else
{
t = SingleRightRotation(t);
printf("【注意】插入过程中出现了右右不平衡\n");
}
}
}
//else t->data == val 说明此树中已经有该数据了,无需插入,而且根据搜索树的用途以及定义,也不应该进行插入
t->Height = Max(getHeight(t->Left), getHeight(t->Right)) + 1; //针对于没有出现不平衡的情况,更新一下该结点记录的树高,
//此处必须使用getHeight函数,而不能使用结点的Height参数,因为t的左右指针可能为NULL,会导致非法访问0地址
return t;
}
主函数测试
#define maxop 20
int main()
{
srand((unsigned)time(NULL));
int val, op, i = 0;
AVLTree t = NULL;
for (i; i < maxop; i++)
{
val = rand() % 100;
op = rand() % 4;
switch (op)
{
case 0: {
printf("插入元素 %d \n", val);
t = Insert(t, val);
break;
}
case 1: {
printf("插入元素 %d \n", val);
t = Insert(t, val);
break;
}
case 2: {
printf("插入元素 %d \n", val);
t = Insert(t, val);
break;
}
case 3: {
printf("插入元素 %d \n", val);
t = Insert(t, val);
break;
}
}
printf("前序遍历:");
PreorderTravelsal(t);
printf("\n");
printf("中序遍历:");
InorderTravelsal(t);
printf("\n");
printf("后序遍历:");
PostorderTravelsal(t);
printf("\n");
printf("层序遍历:");
LevelTravelsal_Test(t);
printf("\n");
printf("\n");
}
return 0;
}
3.堆
基本介绍
描述
堆为一种考虑了适合于特权需求的数据结构,通常也被称为优先队列(下面使用元素的大小作为优先级)。堆最常使用的结构为二叉树,而且为一棵完全二叉树,所以一般使用顺序存储进行数据存储
堆具有两个特性:
1.结构特性
由于为使用顺序存储实现数据存储的完全二叉树,所以第一个结点的编号从1开始计算,如果一个节点的编号为i,则其左孩子编号为2i,其右孩子编号为2i+1,即堆中一个树节点和其父节点和子节点数据存储位置的关系是明确的
2.部分有序性
任一节点元素的数值和其子节点所存数值相关,具有一定的大小关系,根据大小关系的不同,可以将堆分为最大堆和最小堆
兄弟结点不具有数值相关性,即两个兄弟结点的数值大小关系不定
概念
最大堆:
任一结点的数值大于或者等于其子结点的数值,特点是根结点的数值在整个堆中是最大的
最小堆:
任一结点的数值小于或者等于其子结点的数值,特点是根结点的数值在整个堆中是最小的
哨兵元素:
为位于下标为0的位置的数据,并不是由用户输入进行产生的,在最大堆中具体体现为一个数值大于用户输入的所有数据的元素,在最小堆中具体体现为一个数值小于用户输入的所有数据的元素。哨兵元素在堆插入操作的循环正常停止中发挥着极其重要的作用
小贴士
堆中数组下标为0对应元素赋值一个哨兵元素的意义?
堆的data部分的第一个单元data[0]是不能存放用户输入的数据的,因为完美二叉树的顺序存储方式中,是依靠下标/2或2及2+1来表示父子节点间的逻辑关系的,而依靠该关系的前提就是数据的编号要从1开始进行编号(编号即为数组的下标)
哨兵元素和代码的具体实现,特别是插入代码的实现有关:以最大堆为例,由于在插入一个元素的时候,需要找到这个新元素的合适位置,于是需要将其和父节点,父节点的父结点,父结点的父结点的父结点…依次进行比较,直到找到一个数值比该新元素的数值还大的父结点,才会停止循环比较,确定新元素的位置,但是如果这个新元素恰好比之前插入的所有元素值都大,那其最后就会在下标为1的结点上,和下标为0的结点进行比较,如果下标为0的结点中的那个随机值比该新元素小,那么循环永远不会停止,即如果不在堆中数组下标为0对应元素赋值一个哨兵元素,那么在进行插入操作的时候,可能会出现死循环的现象。反之,如果出现了死循环,应该先检查是否初始化时没有插入哨兵元素
代码实现
最大堆
结构定义
typedef struct HNode
{
int* data;
int capacity; //capacity为能够存储的元素的最大数目
int size; //size为的已存储的元素的个数
}*Heap;
typedef Heap MinHeap;
typedef Heap MaxHeap;
1.最大堆的初始化
Heap Init_Heap(int max)
{
Heap h = (Heap)malloc(sizeof(struct HNode));
h->data = (int*)malloc((max + 1) * sizeof(int)); //注意,max表示用户希望能够存储的最大元素数目,
//但是别忘了,我们要留有一个单元来放置哨兵元素,于是实际要开辟max + 1个空间
h->capacity = max;
h->size = 0;
h->data[0] = 10000; //由于【确定10000大于用户输入的所有元素】,所以将哨兵元素定为10000
return h;
}
2.最大堆的建立(给定一些无序的数据,把它们的顺序进行调整,使得数据结构符合最大堆的定义)
void PorcDown(int index, Heap h)//负责进行以每一个具有子节点的节点为根的子堆的数据调整
{
int x = h->data[index];
int child, parent;
for (parent = index; parent * 2 <= h->size; parent = child)
{
child = parent * 2;
if (child + 1 <= h->size && h->data[child] < h->data[child + 1]) //当child既有左节点,又具有右节点,同时右节点的优先级大于左节点,则把child指向右节点
child++; //child始终指向较大的那个子节点
if (x < h->data[child]) //数据和最大子节点进行比较,根据最大堆的定义,
h->data[parent] = h->data[child]; //如果数据大于等于子节点,说明当前父节点的位置就是该数据应该存放的位置,跳出for循环
//否则把较大的子节点数据赋值给父节点,并移动指针继续向下判断,直到找到合适的数据存放的合适位置
else //if(x >= h->data[child]) 说明找到了合适的位置
break;
}
h->data[parent] = x;
}
Heap build_Heap(Heap h)
{
int i = 0;
for (i = h->size / 2; i > 0; i--) //注意是从下往上(自最后一个具有子节点的节点开始,向前依次调整)进行最大堆的数据调整
PorcDown(i, h);
return h;
}
3.插入数据
bool Insert(Heap h, int val)
{
if (h->size == h->capacity)
return false;
int i = 0;
int start = ++h->size; //把指针指向新的一个单元
for (i = start; val > h->data[i / 2]; i /= 2) //其实这是一个"父慈子孝"的过程,儿子看到父亲的优先级比我小,就会把父亲拉下来,自己跑上去,反复进行这个过程,
h->data[i] = h->data[i / 2]; //直到儿子发现,自己的优先级比父亲小了,干不过父亲了
//(要么是遇到比起大的用户存储的数据,要么是遇到哨兵元素),才会停止这个过程,即结束循环
h->data[i] = val;
return true;
}
4.取出优先级最大的数据
int DeleteMax(Heap h)
{
if (h->size == 0)
return ERROR;
int max = h->data[1]; //注意,有效数据是从下标为1处开始存储的,
//下标为0处存储的是哨兵元素
//以下的代码都是进行最大元素取走以后,剩下的数据进行调整的过程,
//调整的代码和进行最大堆建立的代码基本相同,不再赘述
int parent, child;
int x = h->data[h->size--]; //把顺序存储中的最后一个元素取出,注意最后一个元素的下标就是size,
//因为用户输入的真正的元素是从下标为1的位置开始存储的
for (parent = 1; parent * 2 <= h->size; parent = child)
{
child = parent * 2;
if (child + 1 <= h->size && h->data[child] < h->data[child + 1])
child++;
if (x >= h->data[child])
break;
else //if (x < h->data[child]) 进行数据位置的调整
h->data[parent] = h->data[child];
}
h->data[parent] = x;
return max; //将优先级最大元素进行返回
}
5.打印堆(即顺序存储二叉树的层序遍历)
void Output(Heap h)
{
int i;
printf("最大堆:");
for (i = 1; i <= h->size; i++)
printf(" %d", h->data[i]);
printf("\n");
return;
}
主函数测试
#define maxop 20
int main()
{
srand((unsigned)time(NULL));
int val, op, data, i = 0;
Heap h = Init_Heap(15);
for (i; i < maxop; i++)
{
val = rand() % 100;
op = rand() % 4;
switch (op)
{
case 0: {
printf("插入元素%d %d \n", val, Insert(h, val));
break;
}
case 1: {
data = DeleteMax(h);
printf("取出最大元素 ");
if (data != ERROR)
printf("1\n");
else
printf("0\n");
break;
}
case 2: {
printf("插入元素%d %d \n", val, Insert(h, val));
break;
}
case 3: {
printf("插入元素%d %d \n", val, Insert(h, val));
break;
}
}
printf("层序遍历:");
Output(h);
printf("\n");
}
return 0;
}
最小堆
1.最小堆的初始化
Heap Init_Heap(int max)
{
Heap h = (Heap)malloc(sizeof(struct HNode));
h->data = (int*)malloc((max + 1) * sizeof(int));
h->capacity = max;
h->size = 0;
h->data[0] = -10000; //由于【确定-10000小于用户输入的所有元素】,所以将哨兵元素定为-10000
return h;
}
2.最小堆的建立(给定一些无序的数据,把它们的顺序进行调整,使得数据结构符合最小堆的定义)
void PorcDown(int index, Heap h)
{
int x = h->data[index];
int child, parent;
for (parent = index; parent * 2 <= h->size; parent = child)
{
child = parent * 2;
if (child + 1 <= h->size && h->data[child] > h->data[child + 1])
child++; //child始终指向较小的那个子节点
if (x > h->data[child])
h->data[parent] = h->data[child];
else
break;
}
h->data[parent] = x;
}
Heap build_Heap(Heap h)
{
int i = 0;
for (i = h->size / 2; i > 0; i--)
PorcDown(i, h);
return h;
}
3.插入数据
bool Insert(Heap h, int val)
{
if (h->size == h->capacity)
return false;
int i = 0;
int start = ++h->size;
for (i = start; val < h->data[i / 2]; i /= 2)
h->data[i] = h->data[i / 2];
h->data[i] = val;
return true;
}
4.取出最小的优先级的数据
int DeleteMin(Heap h)
{
if (h->size == 0)
return ERROR;
int min = h->data[1];
int parent, child;
int x = h->data[h->size--];
for (parent = 1; parent * 2 <= h->size; parent = child)
{
child = parent * 2;
if (child + 1 < h->size && h->data[child] > h->data[child + 1])
child++;
if (x <= h->data[child])
break;
else
h->data[parent] = h->data[child];
}
h->data[parent] = x;
return min;
}
5.打印堆(即顺序存储二叉树的层序遍历)
void Output(Heap h)
{
int i;
printf("最小堆:");
for (i = 1; i <= h->size; i++)
printf(" %d", h->data[i]);
printf("\n");
return;
}
主函数测试
#define maxop 20
int main()
{
srand((unsigned)time(NULL));
int val, op, data, i = 0;
Heap h = Init_Heap(15);
for (i; i < maxop; i++)
{
val = rand() % 100;
op = rand() % 4;
switch (op)
{
case 0: {
printf("插入元素%d %d \n", val, Insert(h, val));
break;
}
case 1: {
data = DeleteMin(h);
printf("取出最小元素 ");
if (data != ERROR)
printf("1\n");
else
printf("0\n");
break;
}
case 2: {
printf("插入元素%d %d \n", val, Insert(h, val));
break;
}
case 3: {
printf("插入元素%d %d \n", val, Insert(h, val));
break;
}
}
printf("层序遍历:");
Output(h);
printf("\n");
}
return 0;
}
4.哈夫曼树
基本介绍
描述
哈夫曼树又称为最优二叉树
如果要构造一棵每一个叶子结点都具有权值的二叉树,且叶子结点的数目固定,则我们可以构造出许多棵不同的树,而哈夫曼树为其中带权路径长度最小的树
哈夫曼树具有以下特点:
1.权越小的结点到根节点的路径长度越大
2.如果哈夫曼树有n个叶子结点,则其结点总数为2n-1
3.不存在度为1的结点
概念
路径长度:
结点的路径长度——两个结点间路径上的分支数
树的路径长度——从树根到每一个结点的路径长度之和
权值:
给每一个树结点赋予的具有某种含义的数值
带权路径长度:
结点的带权路径长度——从树根到该结点的路径长度与该结点权值的乘积
树的带权路径长度(WPL)——所有叶子结点的带权路径长度之和
前缀编码:
任一字符的编码都不是其他字符的编码前缀的一种编码方式
前缀码保证绝对不会出现二义性,非前缀码不是必定会出现二义性的,但是即使不出现二义性,非前缀码进行解码的时候,也会有点小难受
哈夫曼编码就是一种前缀编码,通过保证每一个要进行编码的字符对应的结点都是哈夫曼树的叶子结点来确保每一个字符对应的编码都是前缀码
平均编码长度:
每一个字符对应的前缀码的长度乘以该字符出现的概率,再进行相加,得到的即为这些字符的平均编码长度
小贴士
如何在选择题中快速排除不是哈夫曼编码的编码结果?
哈夫曼编码有几个必要条件:
1.哈夫曼编码必定是前缀码
2.哈夫曼编码的结果使权重(在数据传输中具体为字符的出现频率/次数)较大的字符,对应的编码长度要较短
根据这两个条件,应该可以排除大部分错误答案
当然,更加精细的判断,还是要根据题目给出的字符,及各自对应权重,画出哈夫曼树,得到各个字符的哈夫曼编码结果才行
哈夫曼编码的构造过程的解析?
1.对于每一个要进行编码的字符,首先确定它们的权值,接着在观念上要把它们都看作只有一个根节点的二叉树,它们形成了一个二叉树森林
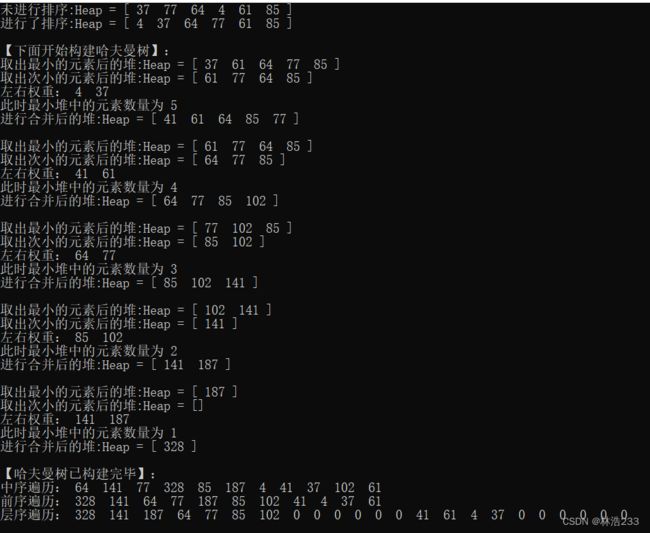
2.取出根结点的权值最小的和次小的树(最小和次小是为了权越小的结点到根节点的路径长度越大),进行一次合并(即以这两个根节点作为一个新结点的子结点,产生一棵新的二叉树),形成的这棵树再放入这个森林中,不断重复这个过程,直到所有的树都合并为一棵树为止,这棵树就是哈夫曼树(对于给定的一些字符及其权值,构造出来哈夫曼树可能不止一棵,因为具体的构造过程可能有所不同)
3.此时,你会发现,所有要进行编码的字符对应的结点,都是这颗树的叶子结点(保证编码结果为前缀码),我们将这颗树的各个分支都赋予一个1/0的二进制数字,则此时根节点到每一个叶子结点的路径上的二进制数的序列就是各叶子结点对应字符的哈夫曼编码结果
哈夫曼编码的构造过程代码的解析?
1.初始化一个元素为哈夫曼树结点指针的最小堆,并进行用户数据输入:
构建一个最小堆的框架,读入用户输入的权值(代码中直接使用随机数),输入进每一个哈夫曼结点的数据区域中
2.进行最小堆的建立:
通过比较各个哈夫曼结点的权值,将权值在不同哈夫曼结点之间进行移动,建立一个以权值作为优先级的最小堆
3.把最小堆的第一个元素指针取出(即取出权值最小的哈夫曼结点A指针),进行最小堆中的各个元素所存指针的移动调整,保证符合最小堆定义
4.再把最小堆的第一个元素指针取出(即取出权值次小的哈夫曼结点B指针),进行最小堆中的各个元素所存指针的移动调整,保证符合最小堆定义
5.初始化一个新的哈夫曼结点C,这个结点的权重为从堆中取出的哈夫曼结点A、B的权重之和,并将哈夫曼结点A、B作为新结点C的子节点,接着把新结点C插入到最小堆中,进行最小堆中的各个元素所存指针的移动调整,保证符合最小堆定义
6.循环进行3、4、5步,直到堆中只有一个结点时候,结束循环,哈夫曼树构建完毕
代码实现
结构定义
//哈夫曼树节点结构定义
typedef struct HTNode* PtrToHTNode;
typedef struct HTNode* HTree;
struct HTNode
{
int weight;
struct HTNode* Right;
struct HTNode* Left;
};
//最小堆结构定义,每一个数据区的元素都是一个指向一个哈夫曼树节点的指针,每一个元素比较大小比较的是权重
typedef struct HNode
{
PtrToHTNode* data;
int max;
int size;
}*Heap;
typedef Heap MinHeap;
初始化哈夫曼树结点
PtrToHTNode Init_HTNode(int val)
{
PtrToHTNode n = (PtrToHTNode)malloc(sizeof(struct HTNode));
n->weight = val;
n->Right = n->Left = NULL;
return n;
}
最小堆的基本函数(为了契合哈夫曼树,做了一些修改)
1.初始化最小堆(哈夫曼树版)
Heap Init_Heap(int max)
{
int i = 0;
Heap h = (Heap)malloc(sizeof(struct HNode));
h->max = max;
h->size = 0;
h->data = (PtrToHTNode*)malloc((1 + h->max) * sizeof(PtrToHTNode));
for (i = 0; i <= h->max; i++)
h->data[i] = Init_HTNode(0);
h->data[0]->weight = -1000;
return h;
}
2.最小堆的建立(哈夫曼树版)
//使一个数组中的数据能够满足最小堆定义的代码
void PercDown(Heap h, int index) //最小堆的建立 1
{
int x = h->data[index]->weight;
int parent, child;
for (parent = index; parent * 2 <= h->size; parent = child)
{
child = parent * 2;
if (child + 1 <= h->size && h->data[child]->weight > h->data[child + 1]->weight) //比较的是各个哈夫曼结点的【权重】
child++;
if (h->data[child]->weight < x)
h->data[parent]->weight = h->data[child]->weight; //调整的是各个哈夫曼结点的【权重】
else
break;
}
h->data[parent]->weight = x;
return;
}
void BuildHeap(Heap h) //最小堆的建立 2
{
int i;
for (i = h->size / 2; i > 0; i--)
PercDown(h, i);
return;
}
3.取出具有最小权重的哈夫曼结点(哈夫曼树版)
//堆的数据删除的代码
HTree DeleteMin(Heap h)
{
if (h->size == 0)
{
printf("堆已空,无最小值");
return NULL;
}
HTree min = h->data[1];
HTree x = h->data[h->size--];
int parent, child;
for (parent = 1; parent * 2 <= h->size; parent = child)
{
child = parent * 2;
if (child + 1 <= h->size && h->data[child]->weight > h->data[child + 1]->weight) //比较的是各个哈夫曼结点的【权重】
child++;
if (x->weight <= h->data[child]->weight)
break;
else
h->data[parent] = h->data[child]; //调整的是各个单元存储的哈夫曼结点【地址】
}
h->data[parent] = x; //调整的是各个单元存储的哈夫曼结点【地址】
return min; //将哈夫曼结点的【地址】进行返回
}
4.向堆中插入哈夫曼结点(哈夫曼树版)
//堆的数据插入的代码
void Insert(Heap h, PtrToHTNode val)
{
if (h->size == h->max)
{
printf("堆已满,无法插入元素");
return;
}
int index = 0;
for (index = ++h->size; val->weight < h->data[index / 2]->weight; index /= 2) //比较的是各个哈夫曼结点的【权重】
h->data[index] = h->data[index / 2]; //调整的是各个单元存储的哈夫曼结点【地址】
h->data[index] = val; //调整的是各个单元存储的哈夫曼结点【地址】
}
5.打印堆(一棵完全二叉树的层序遍历)
void Output(Heap h)
{
int i = 0;
printf("Heap = [");
for (i = 1; i <= h->size; i++)
printf(" %d ", h->data[i]->weight);
printf("]\n");
return;
}
构建一棵哈夫曼树的主函数测试
#include效果
来自作者的话:
此文章的内容还在逐步修进中,希望各位读者可以不吝赐教,有问题都可以在评论区提出来,我看到了会尽快进行更改
于 2022/12/5 第一次整改完毕