ABM论文翻译
文章目录
-
- 一、Abstract
- 二、Introduction
- 三、Method
-
- 3.1、特征提取模块(Feature Extraction Modul)
- 3.2、注意聚合模块(Attention Aggregation Module)
- 3.3、双向互学习模块(Bi-directional Mutual Learning Module)
- 3.4、损失函数(Loss Function)
- 四、Experiments
论文地址: https://arxiv.org/pdf/2112.03603.pdf
项目地址:https://github.com/XH-B/ABM
一、Abstract
本文提出一种基于双向交互学习的注意力聚合模型(ABM),这个模型由两个并行且方向相反的编码器(L2R和R2L)组成。这两个编码器通过相互蒸馏,使得在每一步一对一信息传递的训练中,两个方向的互补信息被充分利用。另外,为了处理不同尺度的数学符号,本文提出了注意力聚合模型(AAM),这个模型能够聚合不同尺度下的注意力。值得注意的是,在推理阶段,考虑到模型已经从两个方向学习知识,所以只使用L2R部分的分支进行推理,这样能够保持了原始参数的大小和推理速度。
二、Introduction
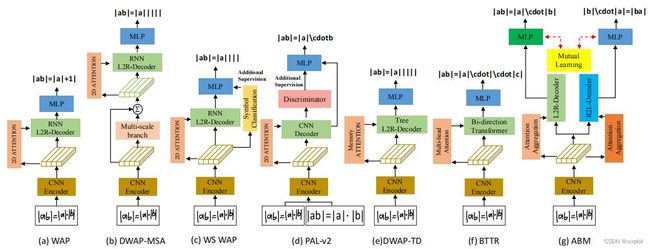
WAP首先引入了二维注意力,以解决空间位置覆盖不足的问题,如下图1所示二维注意关注的是过去的总和,旨在跟踪过去的对齐信息,这样注意模型就可以被引导,将更高的注意概率分配给图像的非翻译区域。然而,这种方式的主要限制是,它只使用历史对齐信息,而不考虑未来的信息(非翻译区域)。如,许多数学表达式都是对称结构,其中左“{”和右“}”括号总是出现在一起,有时相距很远。方程中的一些符号是相关的,比如 f f f和 d x dx dx。大多数方法只使用从左到右的注意力来识别当前的符号,而忽略了来自右边的未来信息,这可能会导致注意力漂移。而符号与之前符号之间的依赖信息随着其距离的增加而变弱。因此,他们没有充分利用长距离相关性或数学表达式的语法规范。
BTTR使用带有两个方向的transformer解码器来解决注意力漂移的问题,但没有有效的让BTTR学习反方向监督信息,并且BTTR在整个学习的过程中没有对齐注意力,这使得它在识别长公式中任然受到限制。
DWAP-MSA通过对编码添加多尺度特征来缓解数学表达式中字符尺度的变化而导致识别困难或不确定性的问题。然而,它们并不缩放局部的接受域,而只缩放特征图,这使得在识别过程中不可能准确地关注小字符。
因此,我们提出了ABM框架,该框架包含三个模型:(1)特征提取。使用DenseNet提取特征;(2)注意力聚合模块(Attention Aggregation module)。我们提出了多尺度注意,在数学表达式中识别不同大小的字符,从而提高了当前的识别精度,缓解了误差积累的问题。(3)双向学习模块( Bi-directional Mutual Learning module)。我们提出了一种新的解码器框架,有两个相反解码方向的并行解码器分支(L2R和R2L),并使用相互蒸馏相互学习。注意,虽然我们使用两个解码器进行训练,但我们只使用一个L2R分支进行推理。
三、Method
我们提出了一种新的端到端注意聚合和双向互学习(ABM)架构,如图2所示。它主要由三个模块组成:
-
特征提取模块(FEM),该模块能从一个数学表达式图像中提取特征信息。
-
注意聚合模块(AAM)集成多尺度覆盖注意,对齐历史注意信息,在解码阶段有效地聚合不同大小符号的不同尺度特征。
-
双向互学习模块(BML)由两个解码方向相反的并行译码器(L2R和R2L)组成,以相互补充信息。在训练过程中,每个解码器分支不仅可以学习真实的latex序列,还可以学习相反latex的序列,从而提高解码能力。

3.1、特征提取模块(Feature Extraction Modul)
使用DenseNet提取特征,输出 H × W × D H \times W \times D H×W×D,我们编码信息转化M维( M = H × W M=H \times W M=H×W),得到输出向量为 a = ( a 1 , a 2 , … , a M ) a=(a_{1},a_{2},\dots,a_{M} ) a=(a1,a2,…,aM)。
3.2、注意聚合模块(Attention Aggregation Module)
注意力机制能够指导编码器更加关注输入图片的特定区域。尤其是基于全局的注意力机制,它能更好的跟踪对齐信息并指导模型对待翻译区域分配更高的注意机率。受此启发,我们提出了AAM模块在全局注意力上聚合不同的感受野。与传统的注意力机制不同,AAM不仅关注局部的信息,同时也关注在更大感受野上的全局信息。因此,AAM将产生更精细的对齐信息,并帮助模型捕获更准确的空间关系。 不同于DWAP-MSA模型通过将dense编码器的多尺度分支来生成低级和高级特征,AAM提出一种将隐藏状态 h t h_{t} ht、特征图 F F F和全局注意 β t \beta_{t} βt计算当前注意力权值 α t \alpha_{t} αt,然后得到上下文向量 c t c_{t} ct。
A s = U s β t , A l = U l β t β t = ∑ l = 1 t − 1 α l A_{s} = U_{s}β_{t}, A_{l} = U_{l}β_{t} \\ β_{t}=\sum^{t-1}_{l=1}\alpha_{l} As=Usβt,Al=Ulβtβt=l=1∑t−1αl
U s U_{s} Us和 U l U_{l} Ul分别表示小核和大核(如5、11)的卷积运算, β t β_{t} βt表示过去所有注意概率之和,初始化为零向量。其中, α l α_{l} αl为第 l l l步的注意力得分。
所以,当前的注意力 α t α_{t} αt计算过程如下:
α t = v a T t a n h ( W h h t + U f F + W s A s + W l A l ) \alpha_{t}=v^{T}_{a}tanh(W_{h}h_{t}+U_{f}F+W_{s}A_{s}+W_{l}A_{l}) αt=vaTtanh(Whht+UfF+WsAs+WlAl)
最终的上下文向量 c t c_{t} ct为特征信息 a a a与注意t力 α t α_{t} αt的加权和,计算公式如下:
c t = ∑ i = 1 M α t , i a i c_{t}=\sum^{M}_{i=1}\alpha_{t,i}a_{i} ct=i=1∑Mαt,iai
3.3、双向互学习模块(Bi-directional Mutual Learning Module)
给定一个数学公式输入图像,传统的方法是从左到右解码(L2R),这种方式没有考虑长距离依赖的问题。因此我们提出双向解码器将输入图像翻译成两个相反方向(L2R 、R2L)的Latex序列,然后互相学习解码信息。这两个分支具有相同的架构,只是在其解码方向上不同。
对于双向训练,我们分别添加 < s o s >
从左到右(L2R)表示: y = ( < s o s > , Y 1 , Y 2 , . . . , Y T , < e o s > ) y=(
从右到左(R2L)表示: y = ( < e o s > , Y T , Y T − 1 , . . . , Y 1 , < e o s > ) y=(
L2R和R2L分支在步骤t处预测的概率计算如下:
p ( y ⃗ ∣ y ⃗ y − 1 ) = W o m a x ( W y E y ⃗ t − 1 + W h h t + W t c t ) p ( y ← ∣ y ← y − 1 ) = W o ′ m a x ( W y E ′ y ← t − 1 + W h ′ h t ′ + W t ′ c t ′ ) p(\vec y|\vec y_{y-1})=W_{o}max(W_{y}E \vec y_{t-1}+W_{h}h_{t}+W_{t}c_{t}) \\ p(\overleftarrow y|\overleftarrow y_{y-1})=W^{'}_{o}max(W_{y}E^{'} \overleftarrow y_{t-1}+W^{'}_{h}h^{'}_{t}+W^{'}_{t}c^{'}_{t}) p(y∣yy−1)=Womax(WyEyt−1+Whht+Wtct)p(y∣yy−1)=Wo′max(WyE′yt−1+Wh′ht′+Wt′ct′)
其中, h t h_{t} ht、 y ⃗ t \vec y_{t} yt表示L2R分支中步骤t的当前状态和之前的预测输出。 ∗ ′ *' ∗′表示R2L分支。 W o ∈ R K × d W_{o}\in R^{K\times d} Wo∈RK×d, W y ∈ R d × n W_{y}\in R^{d \times n} Wy∈Rd×n、 W h ∈ R d × n W_{h} \in R^{d \times n} Wh∈Rd×n和 W d × D W^{d \times D} Wd×D是可训练矩阵。d、K和n分别表示注意力维数、所有标签类数和GRU的维数。E是一个嵌入矩阵。Max表示最大值激活函数。隐藏表示 { h 1 、 h 2 、 . . . , h t } \{h1、h2、...,ht\} {h1、h2、...,ht}由:
h ^ t = f 1 ( h t − 1 , E y ⃗ t − 1 ) , h t = f 2 ( h ^ t , c t ) \widehat h_{t} =f_{1}(h_{t-1},E \vec y_{t-1}), \\ h_{t}=f_{2}(\widehat h_{t},c_{t}) h t=f1(ht−1,Eyt−1),ht=f2(h t,ct)
我们定义L2R分支的概率为 p ⃗ l 2 r = { < s o s > , y ⃗ 1 , y ⃗ 2 , . . . , y ⃗ T , < e o s > } \vec p_{l2r}= \{
σ ( z ⃗ i , k , S ) = e x p ( z ⃗ i , k ) / S ∑ j = 1 K e x p ( Z ⃗ i , j / S ) \sigma(\vec z_{i,k},S)=\frac{exp(\vec z_{i,k})/S}{\sum^{K}_{j=1}exp(\vec Z_{i,j}/S)} σ(zi,k,S)=∑j=1Kexp(Zi,j/S)exp(zi,k)/S
其中,S表示生成软标签的参数。由解码器网络计算出的该序列的第 i i i个符号的对数被定义为 z i = { z 1 , z 2 , . . . , z K } z_{i}=\{z_{1},z_{2},...,z_{K}\} zi={z1,z2,...,zK}。我们的目标是最小化两个分支概率分布之间的距离。因此, p ⃗ l 2 r \vec p_{l2r} pl2r与 P ← r 2 l ∗ \overleftarrow P^{∗}_{r2l} Pr2l∗之间的KL距离计算如下:
L K L = S 2 ∑ i = 1 T ∑ j = 1 K σ ( Z ⃗ i , j , S ) l o g σ ( Z ⃗ i , j , S ) σ ( Z ← T + 1 − i , j , S ) L_{KL}= S^{2}\sum^{T}_{i=1}\sum^{K}_{j=1}\sigma(\vec Z_{i,j},S)log\frac{\sigma(\vec Z_{i,j},S)}{\sigma(\overleftarrow Z_{T+1-i,j},S)} LKL=S2i=1∑Tj=1∑Kσ(Zi,j,S)logσ(ZT+1−i,j,S)σ(Zi,j,S)
3.4、损失函数(Loss Function)
特别地,对于长度为T的Latex序列 y ⃗ l 2 r = { < s o s > , Y 1 , Y 2 , . . . , Y T , < e o s > } \vec y_{l2r}=\{
y ⃗ i , k = e x p ( Z ⃗ i , k ) ∑ j = 1 K e x p ( Z ⃗ i , j ) \vec y_{i,k}=\frac{exp(\vec Z_{i,k})}{\sum^{K}_{j=1}exp(\vec Z_{i,j})} yi,k=∑j=1Kexp(Zi,j)exp(Zi,k)
对于多分类,目标标签与两个分支的softmax概率之间的交叉熵损失定义为:
L c e l 2 r = ∑ i = 1 T ∑ j = 1 K − Y i , j l o g ( y ⃗ i , j ) L c e r 2 l = ∑ i = 1 T ∑ j = 1 K − Y i , j l o g ( y ← T + 1 − i , j ) L^{l2r}_{ce}=\sum^{T}_{i=1}\sum^{K}_{j=1}-Y_{i,j}log(\vec y_{i,j}) \\ L^{r2l}_{ce}=\sum^{T}_{i=1}\sum^{K}_{j=1}-Y_{i,j}log(\overleftarrow y_{T+1-i,j}) Lcel2r=i=1∑Tj=1∑K−Yi,jlog(yi,j)Lcer2l=i=1∑Tj=1∑K−Yi,jlog(yT+1−i,j)
全局的损失函数为:
L = L c e l 2 r + L c e r 2 l + λ L K L L=L^{l2r}_{ce}+L^{r2l}_{ce}+\lambda L_{KL} L=Lcel2r+Lcer2l+λLKL
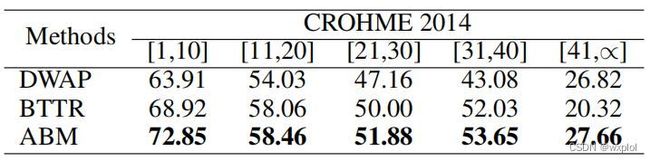
四、Experiments