数据分析大赛医药电商问题——时间序列SARIMA模型
日志
这次参加数据分析大赛,获得了一等奖,有些心得聊以分享。一方面记录自己在数据挖掘处理方面的学习成果,另一方面也给刚踏足数据分析方面有学习困扰的uu们一些启发。这次比赛,我主要用的分析工具是Python,主要用到的库是Numpy,matplotlib,pandas,seaborn还有一系列时间序列分析相关的库,代码中会提到。主要用到的方法有pandas库的分类汇总,matplotlib和seaborn库的数据可视化和完整的一套时间序列拟合分析流程。希望大家看我的文章可以有所收获,也希望行业大佬们看到可以给我一些指导意见。
问题重述
data数据如下所示:
店铺情况分析
文本处理函数
在discount一栏我将文本转换成数字时遇到了困难,发现用int函数不能直接转换,因此我自己写了一个函数,主要思想是将discount栏下的字符串先分割,然后提取出其中的数字。
## 文本转化数字处理函数
def text_convert2num(series):
series_pro = series.str.split('')
series_wanted = []
i = 0
k = len(series)
while i < k:
if len(series_pro[i]) == 4:
wanted = eval(series_pro[i][1])
elif len(series_pro[i]) == 6:
wanted = eval(series_pro[i][1]) + 0.1*eval(series_pro[i][3])
else:
wanted = 10
series_wanted.append(wanted)
i = i+1
return series_wanted
销售额条形图
销售额是一个新指标,是将price、sold和discount相乘得到。通过groupby函数分类汇总得到各店铺的销售额后便可以绘制条形图了。为了直观看出市场分配比例,还可以用饼图进行可视化。
## 销售额对店铺的分类汇总及可视化
sell_agg = data.groupby('shop_name')['销售额'].sum()
sell_agg = sell_agg.sort_values(ascending=False)
shop_pie_data = sell_agg.head(10)
shop_pie_data['其他'] = sum(sell_agg[10:])
shop_pie_data = shop_pie_data.sort_values(ascending=False)
plt.figure(dpi=400,figsize=(15,10))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
X = shop_pie_data.index # X轴数据
Y = shop_pie_data # Y轴数据
plt.style.use('ggplot') # 添加网格线
plt.title("销售额图表") # 柱状图标题
plt.xlabel("店名") # X轴名称
plt.ylabel("销售额") # Y轴名称
plt.xticks(rotation = 90)
plt.plot(X, Y, color="blue") # 绘制柱状
plt.bar(X,Y)
plt.figure(dpi=400,figsize=(15,10))
explode = (0.1,0.1,0,0,0,0,0,0,0,0,0)
plt.pie(Y,labels=X,autopct='%3.1f%%',shadow=True,explode=explode)
plt.tight_layout()
销售额时序图
时序图的做法就是按date_time字段对销售额进行分类汇总,得到的数据可以直接用matplotlib作图。
## 销量最好的药店时序图绘制
data2 = data.loc[data['shop_name'] == '阿里健康大药房',:]
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
sell_time = data2.groupby('date_time')['销售额'].sum()
X = sell_time.index # X轴数据
Y = sell_time # Y轴数据
plt.style.use('ggplot') # 添加网格线
plt.title("销售额图表") # 柱状图标题
plt.xlabel("日期") # X轴名称
plt.ylabel("销售额") # Y轴名称
plt.xticks(rotation = 90)
plt.plot(X, Y, color="red") # 绘制折线图药品分析
字符切片函数
该函数主要用于分析parameter函数中的信息。由于parameter函数中分隔符众多,不能通过一个split解决,因此在一次切片后,我利用for循环对每行进行了二次切片,将切片内容以列表形式放入parameter中。
## 字符串二分割处理函数
def colon_split(line,matrix):
row = matrix[line]
temp = []
for i in range(len(row)):
element = row[i].split(':')
temp.append(element)
row = temp
temp2 = []
for j in range(len(row)):
for m in range(2):
temp2.append(row[j][m])
matrix[line] = temp2
return matrix[line] 药品名称提取函数
关于药品有2个指标可以用来分析,一个是parameter中的药品名称,另一个是药品id。为了提取药品名称,我编写了如下函数,基于切片函数操作过的parameter通过索引提取出药品名称。
## 药品名称填充函数
def medicine_fill(matrix,line):
row = matrix[line]
position = 0
if row.count('药品名称'):
position = row.index('药品名称')
medicine_name = row[position+1]
else:
medicine_name = '无具体药品名称'
return medicine_name药品月销售额时序图绘制函数
此处作图用的标准是药品id。传统的matplotlib作图,不再赘述。
# 药品月销售额曲线绘制函数
def id_plot(a):
id = id_select[a]
data3 = data.loc[data['id'] == id]
monthly_sell = data3.groupby('date_time')['销售额'].sum()
X = monthly_sell.index # X轴数据
Y = monthly_sell # Y轴数据
plt.style.use('ggplot') # 添加网格线
plt.title("销售额图表") # 柱状图标题
plt.xlabel("日期") # X轴名称
plt.ylabel("销售额") # Y轴名称
plt.xticks(rotation = 90)
plt.plot(X, Y, color="red",marker='o') # 绘制柱状
品牌分析
品牌提取函数
原理与药品名称提取函数类似,不再赘述。
## 品牌名称填充函数
def brand_fill(matrix,line):
position = 0
row = matrix[line]
if row.count('品牌'):
position = row.index('品牌')
brand_name = row[position+1]
else:
brand_name = '无具体品牌名称'
return brand_name堆面积图
堆面积图用于分析对比两张折线图非常好用。用的是stackplot函数。
## 分析十大品牌销量最好的原因
## 原因1: 药品销售种类广泛
top10brand_data = data.loc[data['brand'] == top10brand[0],:]
for i in range(1,10):
data_temp = data.loc[data['brand'] == top10brand[i],:]
top10brand_data = pd.concat([top10brand_data,data_temp])
else_brand = sell_well_brand_sorted[10:]
else_brand = else_brand.index
else_brand_data = data.loc[data['brand'] == else_brand[0],:]
for i in range(1,526):
data_temp = data.loc[data['brand'] == else_brand[i],:]
else_brand_data = pd.concat([else_brand_data,data_temp])
## 时间维度:堆面积图绘制
header = top10brand_data.groupby('date_time')['销售额'].sum()
tailer = else_brand_data.groupby('date_time')['销售额'].sum()
X = header.index
Y = np.vstack([header.tolist(),tailer.tolist()])
plt.figure(dpi=400,figsize=(12,8))
plt.title('销量堆面积图')
plt.xlabel('月份')
plt.ylabel('销量')
labels=['前十','其他']
plt.stackplot(X,Y,labels=labels)
plt.legend(loc='upper left')SARIMA
时序图
该时序图就是我们需要进行预测的原材料,先画出来康康。
sale_time_series = data.groupby('date_time')['销售额'].sum()
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
X = sale_time_series.index # X轴数据
Y = sale_time_series # Y轴数据
plt.style.use('ggplot') # 添加网格线
plt.title("总销售额时序图") # 柱状图标题
plt.xlabel("日期") # X轴名称
plt.ylabel("销售额") # Y轴名称
plt.xticks(rotation = 90)
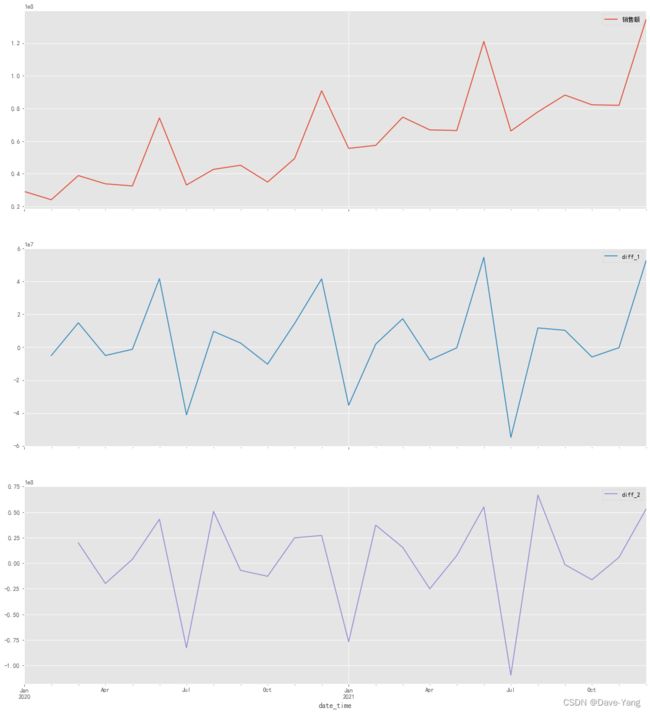
plt.plot(X, Y, color="red") # 绘制折线图序列差分
即对时间序列进行一阶差分和二阶差分,看看是否平稳。一般情况下,一阶差分就够了。科学起见,用平稳性检验再分析一下。
ts = sale_time_series
n_sample = ts.shape[0]
n_train = int(0.9 * n_sample)+1
n_forecast = n_sample - n_train
ts_train = ts.iloc[:n_train]
ts_test = ts.iloc[n_train:]
diff_df = ts.copy()
diff_df.index = ts.index
diff_df = pd.DataFrame(diff_df)
# 一阶差分
diff_df['diff_1'] = diff_df.diff(1).dropna()
# 二阶差分
diff_df['diff_2'] = diff_df['diff_1'].diff(1).dropna()
# 作图
plt.figure(dpi=400,figsize=(12,8))
diff_df.plot(subplots=True,figsize=(18,20))
plt.show()
''' 通过作图不难发现,一阶差分的时序图已经十分平稳,因此采用一阶差分的进行分析'''
ts_diff=ts.copy()
ts_diff.index=ts.index
ts_diff=ts.diff(1).dropna()
plt.plot(ts_diff)平稳性检验
平稳性检验最重要的是P值,如果P值小于0.05检验通过。
## 平稳性检验
from statsmodels.tsa.stattools import adfuller
ADF1 = adfuller(ts) # 原始数据
ADF1 = pd.DataFrame(ADF1)
ADF1.to_excel('ADF_original_series.xlsx')
ADF2 = adfuller(diff_df['diff_1'].dropna()) # 一阶差分
ADF2 = pd.DataFrame(ADF2)
ADF2.to_excel('ADF_diff1.xlsx')
ADF3 = adfuller(diff_df['diff_2'].dropna()) # 二阶差分
ADF3 = pd.DataFrame(ADF3)
ADF3.to_excel('ADF_diff2.xlsx')白噪声检验
时间序列有2次白噪声检验,这是第一次。这一次的目的是为了验证该序列不是随机序列。因为随机序列是没有办法进行建模分析的。也是看显著性水平(lb_value)是否小于0.05,如果个延迟系数下的显著性水平均小于0.05,则该序列不是随机序列,检验通过。
## 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(ts_diff, lags = 10)
ACF和PACF图
ACF和PACF图用于确定模型中p和q两个参数,但一般很少通过图像去直接确定。而是通过AIC和BIC准则去具体判断。该类图中横坐标为延迟系数,纵坐标为误差浮动值。定阶原则如下:
| ARIMA模型定阶原则 |
||
| 模型 |
自相关系数 |
偏自相关系数 |
| AR(p) |
拖尾 |
P阶截尾 |
| MA(q) |
q阶截尾 |
拖尾 |
| ARMA(p,q) |
拖尾 |
拖尾 |
## 绘制ACF和PACF图
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plt.figure(dpi=1000,figsize=(12,8))
pacf = plot_pacf(ts_diff, lags=10)
plt.title('PACF')
pacf.show()
plt.figure(dpi=1000,figsize=(12,8))
acf = plot_acf(ts_diff, lags=10)
plt.title('ACF')
acf.show()时序分解
没啥好多说,SARIMA常规操作。
## 季节性、周期性分解
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts,extrapolate_trend=12)
trend = decomposition.trend # 趋势部分
seasonal = decomposition.seasonal # 季节性部分
residual = decomposition.resid # 残留部分
plt.figure(figsize=(20,8),dpi=400)
decomposition.plot()BIC准则
BIC准则是ARIMA中确定p和q参数的常用方法,具体实现方法如下,该部分代码我是借鉴的,感谢CSDN上的大佬们!!!
# ARIMA参数检索,BIC准则绘制热力图
import itertools
import statsmodels.api as sm
p_min = 0
d_min = 0
q_min = 0
p_max = 2
d_max = 1
q_max = 2
results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
for p,d,q in itertools.product(range(p_min,p_max+1),
range(d_min,d_max+1),
range(q_min,q_max+1)):
if p==0 and d==0 and q==0:
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = np.nan
continue
try:
model = sm.tsa.ARIMA(ts_train, order=(p, d, q),
#enforce_stationarity=False,
#enforce_invertibility=False,
)
results = model.fit()
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = results.bic
except:
continue
results_bic = results_bic[results_bic.columns].astype(float)
fig, ax = plt.subplots(figsize=(10, 8),dpi=400)
ax = sns.heatmap(results_bic,
mask=results_bic.isnull(),
ax=ax,
annot=True,
fmt='.2f',
)
ax.set_title('BIC')
plt.show()AIC准则
与BIC准则类似,用于确定参数。相比于BIC,AIC对于SARIMA模型更加适合。本质上AIC和BIC都是优化模型,要取最小值时候的解。
## 季节性ARIMA参数检索,AIC准则确定季节性参数
import itertools
p = q = range(0, 2) # p、q一般取值不超过2
d = range(1,2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 6) for x in list(itertools.product(p, d, q))]
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(ts_train,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print('ARIMA{}x{} - AIC:{}'.format(param, param_seasonal, results.aic))
except:
continue SARIMA模型建立
SARIMA最后一个周期参数可以观察图像变化周期直接得到。在7个参数都确定后,模型建立、训练然后预测画图。
import statsmodels.api as sm
df = ts
mod = sm.tsa.statespace.SARIMAX(df,order=(1,1,1),seasonal_order=(1, 1, 1, 6),enforce_stationarity=False,enforce_invertibility=False)
result = mod.fit()
pred_all = result.predict()
predict_sunspots = result.forecast(3)
plt.figure(figsize=(12, 8),dpi=400)
plt.plot(df,color='red',marker='o')
plt.plot(pred_all,color='blue',marker='d')
plt.plot(predict_sunspots,color='purple',marker='d')残差有关检验
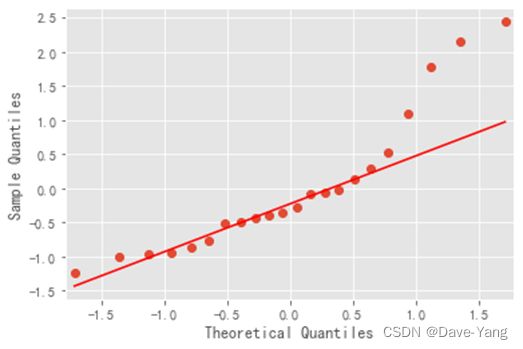
q-q图残差检验
绝大部分服从线性则通过检验,看图即可。
## 残差检验
resid = result.resid
from statsmodels.graphics.api import qqplot
plt.figure(dpi=400,figsize=(12,8))
qqplot(resid, line='q', fit=True) # qq图
plt.show()自相关检验
得到DW=2.394,理论上该值在1~3之间都可以通过检验。
## 自相关性检验
import statsmodels.api as sm
print(sm.stats.durbin_watson(resid.values))白噪声检验
第二次白噪声检验,这次检验是检验的时间序列分解完后没法再分析的渣渣。就是随机的残差序列。因此该检验与第一次相反,要满足Prob值大于0.05。只有剩下的数据无法进行分析,才证明时间序列已经充分建模。
## 白噪声检验
r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
data = np.c_[range(13), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
table = table.set_index('lag')
table.to_excel('白噪声检验.xlsx')| LAG |
AC |
Q |
Prob(>Q) |
| 0 |
-0.2249 |
1.372 |
0.241 |
| 1 |
-0.00351 |
1.372 |
0.503 |
| 2 |
0.058643 |
1.474 |
0.688 |
| 3 |
-0.23874 |
3.252 |
0.516 |
| 4 |
0.264553 |
5.551 |
0.352 |
| 5 |
0.092038 |
5.845 |
0.440 |
| 6 |
-0.06688 |
6.009 |
0.538 |
| 7 |
-0.1085 |
6.468 |
0.594 |
| 8 |
-0.03966 |
6.533 |
0.685 |
| 9 |
0.06213 |
6.705 |
0.752 |
| 10 |
0.019609 |
6.724 |
0.820 |
| 11 |
-0.00561 |
6.726 |
0.875 |
| 12 |
-0.10009 |
7.294 |
0.886 |
模型误差评估
MSE等误差评价指标在本题数值大的情况下显得不直观。因此我采用MAPE指标评估模型误差,该指标得到的结果是个百分比,数值不会非常巨大,更加直观。
## 模型误差评估
from sklearn import metrics
test_diff = ts_diff[-2:]
MSE = metrics.mean_squared_error(df, pred_all)
RMSE = metrics.mean_squared_error(df,pred_all)**0.5
MAE = metrics.mean_absolute_error(df, pred_all)
print(MAE)
print(RMSE)
def mape(y_true, y_pred,n):
res_mape = np.mean(np.abs((y_pred - y_true) / y_true)) * 100 / n
return res_mape
MAPE = mape(df,pred_all,24)
print(MAPE)拟合图像如下:
求得MAPE=0.725%。拟合效果不错。预测值如下:
| 月份 销售额预测值 |
| 2022-01 90232429.06430641元 |
| 2022-02 95922990.24794471元 |
| 2022-03 112387431.26476987元 |
总代码
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
## 数据导入
data = pd.read_excel('data.xlsx')
## 店名描述性统计
shop_cnt = data.groupby('shop_name').count()
shop_num = len(shop_cnt)
shop_name = shop_cnt.index
data['销售额'] = 0
data['药品名称'] = 0
## 文本转化数字处理函数
def text_convert2num(series):
series_pro = series.str.split('')
series_wanted = []
i = 0
k = len(series)
while i < k:
if len(series_pro[i]) == 4:
wanted = eval(series_pro[i][1])
elif len(series_pro[i]) == 6:
wanted = eval(series_pro[i][1]) + 0.1*eval(series_pro[i][3])
else:
wanted = 10
series_wanted.append(wanted)
i = i+1
return series_wanted
## 销售额的计算
series = data['discount'].fillna('无')
discount = text_convert2num(series)
data['discount'] = discount
data_cal = data.iloc[:,[5,6,7]]
sale = []
for i in range(len(data_cal)):
num = data_cal.iloc[i,0]*data_cal.iloc[i,1]*data_cal.iloc[i,2]/10
sale.append(num)
data['销售额'] = sale
## 销售额对店铺的分类汇总及可视化
sell_agg = data.groupby('shop_name')['销售额'].sum()
sell_agg = sell_agg.sort_values(ascending=False)
shop_pie_data = sell_agg.head(10)
shop_pie_data['其他'] = sum(sell_agg[10:])
shop_pie_data = shop_pie_data.sort_values(ascending=False)
plt.figure(dpi=400,figsize=(15,10))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
X = shop_pie_data.index # X轴数据
Y = shop_pie_data # Y轴数据
plt.style.use('ggplot') # 添加网格线
plt.title("销售额图表") # 柱状图标题
plt.xlabel("店名") # X轴名称
plt.ylabel("销售额") # Y轴名称
plt.xticks(rotation = 90)
plt.plot(X, Y, color="blue") # 绘制柱状
plt.bar(X,Y)
plt.figure(dpi=400,figsize=(15,10))
explode = (0.1,0.1,0,0,0,0,0,0,0,0,0)
plt.pie(Y,labels=X,autopct='%3.1f%%',shadow=True,explode=explode)
plt.tight_layout()
## 销量最好的药店时序图绘制
data2 = data.loc[data['shop_name'] == '阿里健康大药房',:]
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
sell_time = data2.groupby('date_time')['销售额'].sum()
X = sell_time.index # X轴数据
Y = sell_time # Y轴数据
plt.style.use('ggplot') # 添加网格线
plt.title("销售额图表") # 柱状图标题
plt.xlabel("日期") # X轴名称
plt.ylabel("销售额") # Y轴名称
plt.xticks(rotation = 90)
plt.plot(X, Y, color="red") # 绘制折线图
## 挑选10个销量最好的药品
id = data.groupby('id').count()
good_num = len(id)
good_sell = data.groupby('id')['销售额'].sum()
good_sell_sorted = good_sell.sort_values(ascending=False)
id_select = []
for i in range(10):
id_select.append(good_sell_sorted.index[i])
# 销量最好的十大药品月销售额曲线绘制函数
def id_plot(a):
id = id_select[a]
data3 = data.loc[data['id'] == id]
monthly_sell = data3.groupby('date_time')['销售额'].sum()
X = monthly_sell.index # X轴数据
Y = monthly_sell # Y轴数据
plt.style.use('ggplot') # 添加网格线
plt.title("销售额图表") # 柱状图标题
plt.xlabel("日期") # X轴名称
plt.ylabel("销售额") # Y轴名称
plt.xticks(rotation = 90)
plt.plot(X, Y, color="red",marker='o') # 绘制柱状
## 十大药品销量时间序列图可视化
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
plt.subplot(2,1,1)
id_plot(0)
plt.subplot(2,1,2)
id_plot(1)
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
plt.subplot(2,1,1)
id_plot(2)
plt.subplot(2,1,2)
id_plot(3)
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
plt.subplot(2,1,1)
id_plot(4)
plt.subplot(2,1,2)
id_plot(5)
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
plt.subplot(2,1,1)
id_plot(6)
plt.subplot(2,1,2)
id_plot(7)
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
plt.subplot(2,1,1)
id_plot(8)
plt.subplot(2,1,2)
id_plot(9)
## 字符串二分割处理函数
def colon_split(line,matrix):
row = matrix[line]
temp = []
for i in range(len(row)):
element = row[i].split(':')
temp.append(element)
row = temp
temp2 = []
for j in range(len(row)):
for m in range(2):
temp2.append(row[j][m])
matrix[line] = temp2
return matrix[line]
## 药品名称填充函数
def medicine_fill(matrix,line):
row = matrix[line]
position = 0
if row.count('药品名称'):
position = row.index('药品名称')
medicine_name = row[position+1]
else:
medicine_name = '无具体药品名称'
return medicine_name
## 品牌名称填充函数
def brand_fill(matrix,line):
position = 0
row = matrix[line]
if row.count('品牌'):
position = row.index('品牌')
brand_name = row[position+1]
else:
brand_name = '无具体品牌名称'
return brand_name
## 品牌和药品名称填充工作
data4 = data['parameter'].str.split('\|\|')
data4 = data4.fillna('无详细信息')
for i in range(len(data4)):
if data4[i] == '无详细信息':
continue
else:
data4[i] = colon_split(i,data4)
for k in range(len(data)):
data.iloc[k,8] = brand_fill(data4,k)
data.iloc[k,11] = medicine_fill(data4,k)
## 药品名称图
medic_data = data.groupby('药品名称')['销售额'].sum()
medic_data = medic_data.sort_values(ascending=False)
medi_data = medic_data.head(10)
else_medi_data = medic_data[10:]
medi_data['其他'] = sum(else_medi_data)
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
plt.xlabel('药品名称')
plt.ylabel('销售额')
plt.title('药品销售额图(按药名参数分类)')
plt.xticks(rotation = 90)
plt.plot(medi_data,color='black')
X = medi_data.index
Y = medi_data
plt.bar(X,Y)
## 销售最高的十大品牌
sell_well_brand = data.groupby('brand')['销售额'].sum()
sell_well_brand_sorted = sell_well_brand.sort_values(ascending=False)
top10brand = sell_well_brand_sorted.head(10).index
## 分析十大品牌销量最好的原因
## 原因1: 药品销售种类广泛
top10brand_data = data.loc[data['brand'] == top10brand[0],:]
for i in range(1,10):
data_temp = data.loc[data['brand'] == top10brand[i],:]
top10brand_data = pd.concat([top10brand_data,data_temp])
else_brand = sell_well_brand_sorted[10:]
else_brand = else_brand.index
else_brand_data = data.loc[data['brand'] == else_brand[0],:]
for i in range(1,526):
data_temp = data.loc[data['brand'] == else_brand[i],:]
else_brand_data = pd.concat([else_brand_data,data_temp])
## 时间维度:堆面积图绘制
header = top10brand_data.groupby('date_time')['销售额'].sum()
tailer = else_brand_data.groupby('date_time')['销售额'].sum()
X = header.index
Y = np.vstack([header.tolist(),tailer.tolist()])
plt.figure(dpi=400,figsize=(12,8))
plt.title('销量堆面积图')
plt.xlabel('月份')
plt.ylabel('销量')
labels=['前十','其他']
plt.stackplot(X,Y,labels=labels)
plt.legend(loc='upper left')
## 空间维度RFM模型
header_price = top10brand_data.groupby('brand')['销售额'].sum()
tailer_price = else_brand_data.groupby('brand')['销售额'].sum()
F1 = header_price.mean()
F2 = tailer_price.mean()
print(F1,F2)
header_sold = top10brand_data.groupby('brand')['sold'].sum()
R1 = header_sold.mean()
tailer_sold = else_brand_data.groupby('brand')['sold'].sum()
R2 = tailer_sold.mean()
header_discount = top10brand_data.groupby('brand')['discount'].count()
tailer_discount = else_brand_data.groupby('brand')['discount'].count()
header_id = top10brand_data.groupby('brand')['id'].count()
tailer_id = else_brand_data.groupby('brand')['id'].count()
## 时间序列分析模型
sale_time_series = data.groupby('date_time')['销售额'].sum()
plt.figure(dpi=400,figsize=(12,8))
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
X = sale_time_series.index # X轴数据
Y = sale_time_series # Y轴数据
plt.style.use('ggplot') # 添加网格线
plt.title("总销售额时序图") # 柱状图标题
plt.xlabel("日期") # X轴名称
plt.ylabel("销售额") # Y轴名称
plt.xticks(rotation = 90)
plt.plot(X, Y, color="red") # 绘制折线图
## ARIMA时间序列预测模型
# 差分序列平稳化
ts = sale_time_series
n_sample = ts.shape[0]
n_train = int(0.9 * n_sample)+1
n_forecast = n_sample - n_train
ts_train = ts.iloc[:n_train]
ts_test = ts.iloc[n_train:]
diff_df = ts.copy()
diff_df.index = ts.index
diff_df = pd.DataFrame(diff_df)
# 一阶差分
diff_df['diff_1'] = diff_df.diff(1).dropna()
# 二阶差分
diff_df['diff_2'] = diff_df['diff_1'].diff(1).dropna()
# 作图
plt.figure(dpi=400,figsize=(12,8))
diff_df.plot(subplots=True,figsize=(18,20))
plt.show()
''' 通过作图不难发现,一阶差分的时序图已经十分平稳,因此采用一阶差分的进行分析'''
ts_diff=ts.copy()
ts_diff.index=ts.index
ts_diff=ts.diff(1).dropna()
plt.plot(ts_diff)
## 平稳性检验
from statsmodels.tsa.stattools import adfuller
ADF1 = adfuller(ts) # 原始数据
ADF1 = pd.DataFrame(ADF1)
ADF1.to_excel('ADF_original_series.xlsx')
ADF2 = adfuller(diff_df['diff_1'].dropna()) # 一阶差分
ADF2 = pd.DataFrame(ADF2)
ADF2.to_excel('ADF_diff1.xlsx')
ADF3 = adfuller(diff_df['diff_2'].dropna()) # 二阶差分
ADF3 = pd.DataFrame(ADF3)
ADF3.to_excel('ADF_diff2.xlsx')
## 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(ts_diff, lags = 10)
## 绘制ACF和PACF图
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plt.figure(dpi=1000,figsize=(12,8))
pacf = plot_pacf(ts_diff, lags=10)
plt.title('PACF')
pacf.show()
plt.figure(dpi=1000,figsize=(12,8))
acf = plot_acf(ts_diff, lags=10)
plt.title('ACF')
acf.show()
## 季节性、周期性分解
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts,extrapolate_trend=12)
trend = decomposition.trend # 趋势部分
seasonal = decomposition.seasonal # 季节性部分
residual = decomposition.resid # 残留部分
plt.figure(figsize=(20,8),dpi=400)
decomposition.plot()
# ARIMA参数检索,BIC准则绘制热力图
import itertools
import statsmodels.api as sm
p_min = 0
d_min = 0
q_min = 0
p_max = 2
d_max = 1
q_max = 2
results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
for p,d,q in itertools.product(range(p_min,p_max+1),
range(d_min,d_max+1),
range(q_min,q_max+1)):
if p==0 and d==0 and q==0:
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = np.nan
continue
try:
model = sm.tsa.ARIMA(ts_train, order=(p, d, q),
#enforce_stationarity=False,
#enforce_invertibility=False,
)
results = model.fit()
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = results.bic
except:
continue
results_bic = results_bic[results_bic.columns].astype(float)
fig, ax = plt.subplots(figsize=(10, 8),dpi=400)
ax = sns.heatmap(results_bic,
mask=results_bic.isnull(),
ax=ax,
annot=True,
fmt='.2f',
)
ax.set_title('BIC')
plt.show()
## ARIMA模型建立
# from statsmodels.tsa.arima.model import ARIMA
# model = ARIMA(ts_train, order=(1,1,1))
# result = model.fit()
# result.summary()
## 季节性ARIMA参数检索,AIC准则确定季节性参数
import itertools
p = q = range(0, 2) # p、q一般取值不超过2
d = range(1,2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 6) for x in list(itertools.product(p, d, q))]
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(ts_train,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print('ARIMA{}x{} - AIC:{}'.format(param, param_seasonal, results.aic))
except:
continue
## SARIMA模型建立与预测
import statsmodels.api as sm
df = ts
mod = sm.tsa.statespace.SARIMAX(df,order=(1,1,1),seasonal_order=(1, 1, 1, 6),enforce_stationarity=False,enforce_invertibility=False)
result = mod.fit()
pred_all = result.predict()
predict_sunspots = result.forecast(3)
plt.figure(figsize=(12, 8),dpi=400)
plt.plot(df,color='red',marker='o')
plt.plot(pred_all,color='blue',marker='d')
plt.plot(predict_sunspots,color='purple',marker='d')
## 残差检验
resid = result.resid
from statsmodels.graphics.api import qqplot
plt.figure(dpi=400,figsize=(12,8))
qqplot(resid, line='q', fit=True) # qq图
plt.show()
## 自相关性检验
import statsmodels.api as sm
print(sm.stats.durbin_watson(resid.values))
## 白噪声检验
r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
data = np.c_[range(13), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
table = table.set_index('lag')
table.to_excel('白噪声检验.xlsx')
## 模型误差评估
from sklearn import metrics
test_diff = ts_diff[-2:]
MSE = metrics.mean_squared_error(df, pred_all)
RMSE = metrics.mean_squared_error(df,pred_all)**0.5
MAE = metrics.mean_absolute_error(df, pred_all)
print(MAE)
print(RMSE)
def mape(y_true, y_pred,n):
res_mape = np.mean(np.abs((y_pred - y_true) / y_true)) * 100 / n
return res_mape
MAPE = mape(df,pred_all,24)
print(MAPE)
结语
希望大家都能有所收获,共同进步。谨以此记录我的一次数据分析大赛历程。