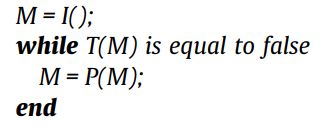智能优化算法(源码)-飞蛾扑火优化算法(MFO)
![]()
获取更多资讯,赶快关注上面的公众号吧!
文章目录
- 灵感
- MFO算法
飞蛾扑火优化算法(Moth-Flame Optimization,MFO)是澳大利亚学者Seyedali Mirjalili于2015年提出的一种受自然生物启发的智能优化算法,该算法的主要灵感来自于飞蛾被称为“横定向”的导航方法。飞蛾在夜间飞行时相对于月亮保持一个固定的角度,这是一种非常有效的远距离直线飞行机制,但是在人造光周围,飞蛾却容易陷入致命的螺旋路径。作者就是模拟了飞蛾的这种特点。扫码关注公众号,后台回复“飞蛾扑火”或“MFO”可以获取Matlab代码和原文。
灵感
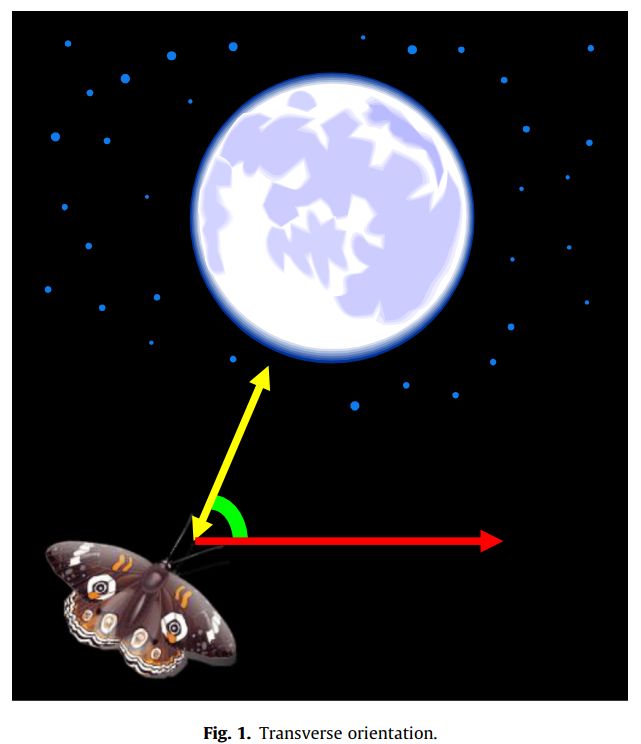
飞蛾最有趣的是它们在夜间的特殊导航方式,它们已经进化到可以利用月光在夜间飞行,这种导航方式叫做横定向。飞蛾飞行时相对于月亮保持一个固定的角度,如图1所示。由于月亮离飞蛾很远,这种机制保证了飞蛾的直线飞行。
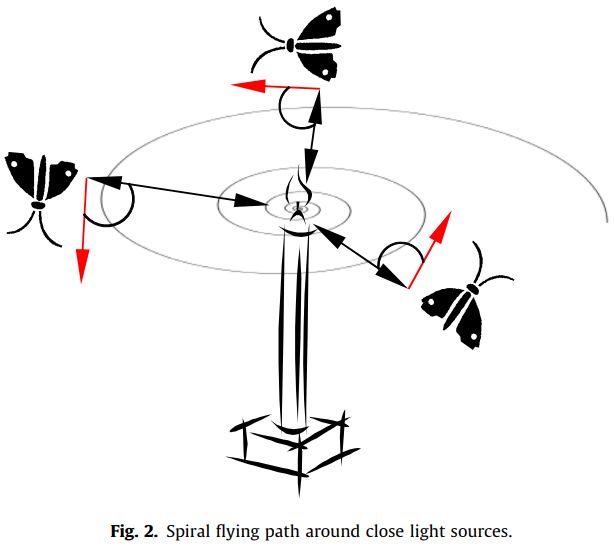
尽管有横定向有一定的作用,但是我们通常观察到蛾子绕着灯光盘旋飞行。事实上,蛾子容易被人造光所欺骗而表现出这样的行为,这是因为只有在光源非常远的情况下横定向才有利于直线移动。当飞蛾看到人造光源时,它们会试图与光源保持相似的角度,以保持直线飞行。然而,由于这种光线与月亮相比非常接近,因此与光源保持类似的角度会导致飞蛾产生无用或致命的螺旋飞行路径,如图2所示。可以看出,蛾子最终会向光线靠拢,作者将这种行为进行数学建模,提出飞蛾扑火优化算法。
MFO算法
在提出的MFO算法中,假设候选解是飞蛾,问题的变量是蛾飞蛾在空间中的位置。因此,飞蛾可以通过改变位置向量在一维、二维、三维或多维空间中飞行。由于MFO算法是一种基于种群的算法,因此飞蛾的集合用如下矩阵表示:
M = [ m 1 , 1 m 1 , 2 ⋯ ⋯ m 1 , d m 2 , 1 m 2 , 2 ⋯ ⋯ m 2 , d ⋮ ⋮ ⋮ ⋮ ⋮ m n , 1 m n , 2 ⋯ ⋯ m n , d ] (1) M=\left[\begin{array}{ccccc} m_{1,1} & m_{1,2} & \cdots & \cdots & m_{1, d} \\ m_{2,1} & m_{2,2} & \cdots & \cdots & m_{2, d} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ m_{n, 1} & m_{n, 2} & \cdots & \cdots & m_{n, d} \end{array}\right] \tag{1} M=⎣⎢⎢⎢⎡m1,1m2,1⋮mn,1m1,2m2,2⋮mn,2⋯⋯⋮⋯⋯⋯⋮⋯m1,dm2,d⋮mn,d⎦⎥⎥⎥⎤(1)
其中 n n n是飞蛾数量, d d d是变量个数即维度。
对于所有的飞蛾,假设存在一个数组用于存储对应的适应度值:
O M = [ O M 1 O M 2 ⋮ O M n ] (2) O M=\left[\begin{array}{c} O M_{1} \\ O M_{2} \\ \vdots \\ O M_{n} \end{array}\right]\tag{2} OM=⎣⎢⎢⎢⎡OM1OM2⋮OMn⎦⎥⎥⎥⎤(2)
另一个关键要素就是火焰,也是一个类似于飞蛾的矩阵:
F = [ F 1 , 1 F 1 , 2 ⋯ ⋯ F 1 , d F 2 , 1 F 2 , 2 ⋯ ⋯ F 2 , d ⋮ ⋮ ⋮ ⋮ ⋮ F n , 1 m n , 2 ⋯ ⋯ F n , d ] (3) F=\left[\begin{array}{ccccc} F_{1,1} & F_{1,2} & \cdots & \cdots & F_{1, d} \\ F_{2,1} & F_{2,2} & \cdots & \cdots & F_{2, d} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ F_{n, 1} & m_{n, 2} & \cdots & \cdots & F_{n, d} \end{array}\right]\tag{3} F=⎣⎢⎢⎢⎡F1,1F2,1⋮Fn,1F1,2F2,2⋮mn,2⋯⋯⋮⋯⋯⋯⋮⋯F1,dF2,d⋮Fn,d⎦⎥⎥⎥⎤(3)
对于火焰,同样假设有一个数组用于存储火焰的适应度值:
O F = [ O F 1 O F 2 ⋮ O F n ] (4) O F=\left[\begin{array}{c} O F_{1} \\ O F_{2} \\ \vdots \\ O F_{n} \end{array}\right]\tag{4} OF=⎣⎢⎢⎢⎡OF1OF2⋮OFn⎦⎥⎥⎥⎤(4)
注意,在飞蛾扑火算法中,飞蛾和火焰都是问题的解,它们之间的区别在于每次更新的方式,飞蛾是在搜索空间中移动的真实的搜索代理,而火焰是飞蛾目前的最优位置。换言之,火焰可以认为是飞蛾打下的标签,因此每只飞蛾围绕火焰搜素,并在找到一个更优解时进行更新。
飞蛾扑火算法可以用一个三元组表示:
M F O = ( I , P , T ) (5) M F O=(I, P, T)\tag{5} MFO=(I,P,T)(5)
其中 I I I用于随机生成飞蛾种群及其对应的适应度值:
I : ∅ → { M , O M } (6) I: \emptyset \rightarrow\{M, O M\}\tag{6} I:∅→{M,OM}(6)
P P P函数是主函数,它在搜索空间内移动飞蛾。这个函数接收矩阵 M M M,并最终返回更新后的矩阵:
P : M → M (7) P: M \rightarrow M\tag{7} P:M→M(7)
T T T函数返回终止条件是否满足:
T : M → { true , false } (8) T: M \rightarrow\{\text { true }, \text { false }\}\tag{8} T:M→{ true , false }(8)
基于 I , P , T I,P,T I,P,T,可以得到飞蛾扑火的一般框架:
函数 I I I用于生成初始解和计算目标值函数,在该函数可以使用任意随机函数,默认如下:
这里存在两个数组 u b ub ub和 l b lb lb,用于定义变量的上界和下界:
u b = [ u b 1 , u b 2 , u b 3 , … , u b n − 1 , u b n ] (9) u b=\left[u b_{1}, u b_{2}, u b_{3}, \ldots, u b_{n-1}, u b_{n}\right]\tag{9} ub=[ub1,ub2,ub3,…,ubn−1,ubn](9)
其中 u b i ub_i ubi为 i i i个变量的上界。
l b = [ l b 1 , l b 2 , l b 3 , … , l b n − 1 , l b n ] (10) l b=\left[l b_{1}, l b_{2}, l b_{3}, \ldots, l b_{n-1}, l b_{n}\right]\tag{10} lb=[lb1,lb2,lb3,…,lbn−1,lbn](10)
其中 l b i lb_i lbi为 i i i个变量的下界。
初始化完成之后,函数 P P P会循环运行直到 T T T函数返回 T r u e True True,其作用就是模拟横定向来进行移动,每只飞蛾相对于火焰的位置可按下式进行更新:
M i = S ( M i , F j ) (11) M_{i}=S\left(M_{i}, F_{j}\right)\tag{11} Mi=S(Mi,Fj)(11)
其中 M i M_i Mi表示第 i i i只飞蛾, F j F_j Fj表示第 j j j个火焰, S S S是螺形函数。
作者选择了对数螺旋作为飞蛾的主要更新机制,当然其他类型的螺旋也是可以的,但是需要满足以下条件:
- 螺旋的起始点应始于飞蛾;
- 螺旋的最终点应该就是火焰的位置;
- 螺旋范围波动不应超过搜索空间。
基于以上几点,对数螺旋可以定义为:
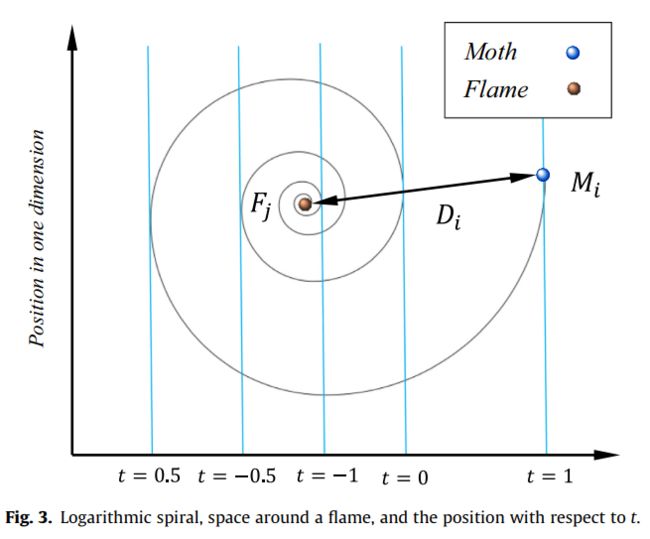
S ( M i , F j ) = D i ⋅ e b t ⋅ cos ( 2 π t ) + F j (12) S\left(M_{i}, F_{j}\right)=D_{i} \cdot e^{b t} \cdot \cos (2 \pi t)+F_{j}\tag{12} S(Mi,Fj)=Di⋅ebt⋅cos(2πt)+Fj(12)
其中 D i D_i Di为第 i i i只飞蛾与第 j j j个火焰之间的距离, b b b是定义螺旋形状的常量, t t t是 [ − 1 , 1 ] [-1,1] [−1,1]之间的随机数。
D D D的计算如下:
D i = ∣ F j − M i ∣ (13) D_{i}=\left|F_{j}-M_{i}\right|\tag{13} Di=∣Fj−Mi∣(13)
公式(12)模拟了飞蛾的螺旋飞行路径,飞蛾的下一位置是根据火焰定义的,参数 t t t定义了飞蛾的下一位置与火焰的位置有多近(-1表示与火焰距离最近,1表示与火焰距离最远)。因此,可以假设火焰周围有一个超椭圆,飞蛾的下一个位置就在这个空间内。螺旋方程允许飞蛾“绕着”火焰飞行,而不一定是在它们之间的空间。这样才能保证搜索空间的探索和利用,如图3所示。
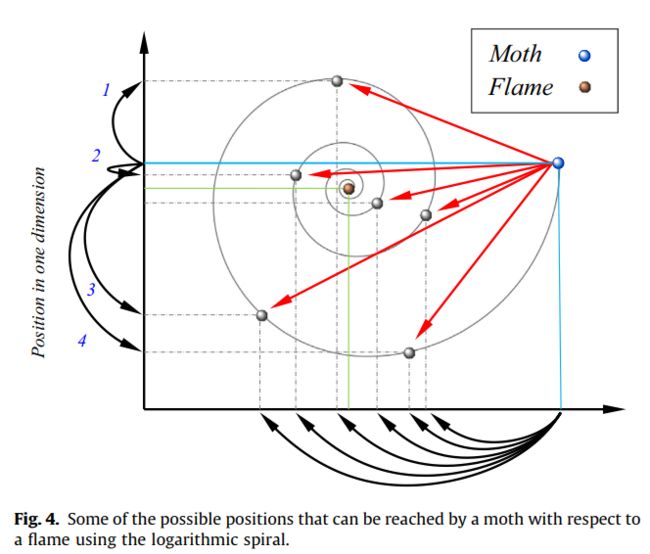
图4为飞蛾在火焰周围位置更新的概念模型,请注意,纵轴只显示了一个维度(给定问题的1个变量/参数),但本文提出的方法可以用来改变问题的所有变量。图4中飞蛾(蓝色水平线)环绕火焰(绿色水平线)可以选择的下一位置(黑色虚线)清楚地表明,飞蛾可以在一维空间内探索和利用火焰周围的搜索空间。当下一个位置在飞蛾和火焰之间的空间之外时,就会发生探索,如1、3、4表示的箭头,当下一个位置位于飞蛾和火焰之间时,就会发生利用,如2表示的箭头。从这个模型中可以发现一些有趣的现象:
- 飞蛾可以通过改变 t t t收敛到火焰附近的任何一点;
- t t t越小,离火焰越近;
- 飞蛾离火焰越近,火焰两侧的位置更新频率越高。
为了进一步加强利用,假设 t t t是 [ r , 1 ] [r,1] [r,1]范围内的随机数,其中 r r r随着迭代的进行线性地从-1降到-2。
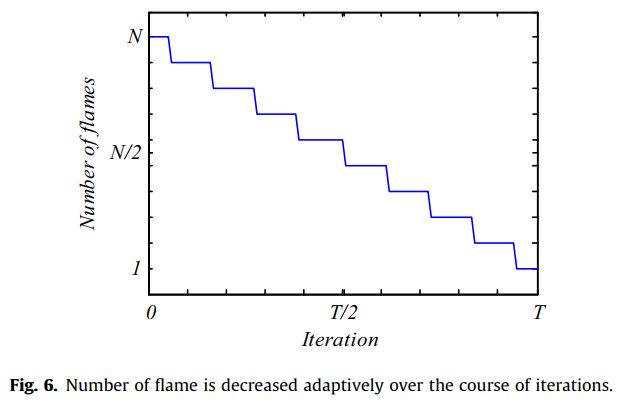
另一个考虑就是飞蛾相对于搜索空间中 n n n个不同位置的位置更新可能会降低对最优解的利用,为了避免这个问题,提出了一种火焰数自适应机制:
flame no = round ( N − l ∗ N − 1 T ) (14) \text { flame no }=\text { round }\left(N-l * \frac{N-1}{T}\right)\tag{14} flame no = round (N−l∗TN−1)(14)
其中, l l l为当前迭代次数, N N N为最大火焰数, T T T为最大迭代次数。
图6显示了在初始迭代时有 N N N个火焰,然而飞蛾的位置更新只和迭代最后几步中的最优火焰有关,火焰数量的逐渐减少就平衡了搜索空间的探索和利用。