经典优化算法之飞蛾扑火(MFO)，原理公式详解，附matlab代码

飞蛾扑火优化算法（Moth-Flame Optimization，MFO）是一种新型元启发式优化算法，该算法是受飞蛾围绕火焰飞行启发而提出的，具有搜索速度快、寻优能力强的特点。该成果于2015年发表在知名SCI期刊Knowledge-Based Systems上。目前谷歌学术上查询被引3575次。

MFO算法通过飞蛾选择火焰、飞蛾围绕火焰飞行、飞蛾扑焰行为，三个主要操作模拟了飞蛾围绕火焰飞行行为，最后选取最优解。

算法原理

（1）飞蛾选择火焰

飞蛾个体表示着优化问题的候选解，飞蛾在优化空间的位置代表求解优化问题的变量，通过在优化空间中改变位置向量来向全局最佳点靠拢，火焰便是飞蛾到当前迭代次数所找到的最佳位置，矩阵M表示飞蛾的位置，数学模型如下式表示：  其中n代表飞蛾的个数；d代表控制变量的数量（维度）；矩阵OM存储飞蛾的适应度值，n代表飞蛾的个数，数学模型如下式表示：  MFO算法中要求每只飞蛾仅利用与之对应的唯一火焰更新其自身位置，从而避免算法陷入局部极值情况，大大增强了算法的全局搜索能力。因此，搜索空间中飞蛾位置与火焰位置是相同维度的变量矩阵矩阵F表示火焰的位置，火焰的适应度值存储在矩阵OF中，数学模型如下式表示：   其中n代表飞蛾的个数；d代表控制变量的数量（维度）。

（2）飞蛾围绕火焰飞行

飞蛾实际上是在搜索空间内移动的搜索个体，每一只飞蛾个体环绕在一个火焰的周围，一旦搜索到更好的解，便更新为下一代中火焰的位置。

MFO算法是近似于优化问题中全局最佳的三元组：  

I是产生一个随机的飞蛾种群和相应的适应度值的函数，其系统模型如下：  P是使飞蛾在搜索空间里移动的主函数。P接受矩阵M，并返回更新后的M。

（3)飞蛾扑焰行为

自然界中具有趋光特性的飞蛾  会朝着距离自身最近的亮光（火焰）  移动。飞蛾扑焰的移动轨迹为选取了对数螺线曲线，算法的对数螺旋曲线定义如下： 这里简单插一嘴：现在很多改进算法都有用到螺旋搜索的思想。可以看到最早的这种螺旋搜索的思想还是来自于飞蛾扑火这种经典算法！不得不感叹一下！

其中：  为飞蛾更新后的位置；Di表示的是第i个飞蛾的位置与第j个火焰的位置之间的距离；b是常量，该常量与螺旋形状相关；t是随机生成的数字，取值区间为［-1,1］，当t=-1时飞蛾离火焰最远，当t =1时飞蛾离火焰最近。  

其中：  为飞蛾  与火焰  的距离。

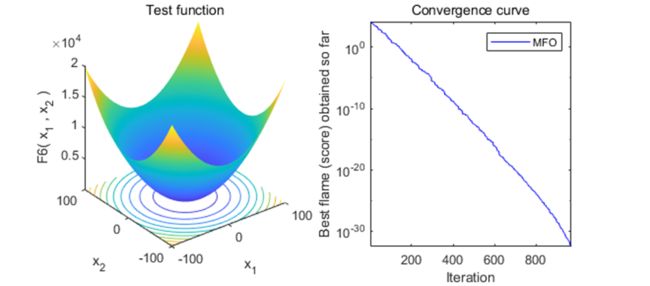
结果展示

以为CEC2005函数集为例，进行结果展示：

 MATLAB核心代码

%% 淘个代码 %%
% 微信公众号搜索：淘个代码，获取更多代码
% 飞蛾扑火优化算法（MFO）
function [Best_flame_score,Best_flame_pos,Convergence_curve]=MFO(N,Max_iteration,lb,ub,dim,fobj,handles,value)


display('MFO is optimizing your problem');


%Initialize the positions of moths
Moth_pos=initialization(N,dim,ub,lb);


Convergence_curve=zeros(1,Max_iteration);


Iteration=1;


% Main loop
while Iterationub;
        Flag4lb=Moth_pos(i,:)Flame_no % Upaate the position of the moth with respct to one flame
                
                % Eq. (3.13)
                distance_to_flame=abs(sorted_population(i,j)-Moth_pos(i,j));
                b=1;
                t=(a-1)*rand+1;
                
                % Eq. (3.12)
                Moth_pos(i,j)=distance_to_flame*exp(b.*t).*cos(t.*2*pi)+sorted_population(Flame_no,j);
            end
            
        end
        
    end
    
    Convergence_curve(Iteration)=Best_flame_score;
    
     if Iteration>2
        line([Iteration-1 Iteration], [Convergence_curve(Iteration-1) Convergence_curve(Iteration)],'Color','b')
        xlabel('Iteration');
        ylabel('Best score obtained so far');        
        drawnow
    end
 
    
    set(handles.itertext,'String', ['The current iteration is ', num2str(Iteration)])
    set(handles.optimumtext,'String', ['The current optimal value is ', num2str(Best_flame_score)])
    if value==1
        hold on
        scatter(Iteration*ones(1,N),All_fitness,'.','k')
    end
    
    Iteration=Iteration+1; 
end

参考文献

[1] Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm[J]. Knowledge-based systems, 2015, 89: 228-249.

完整代码获取方式：后台回复关键字：

TGDM880