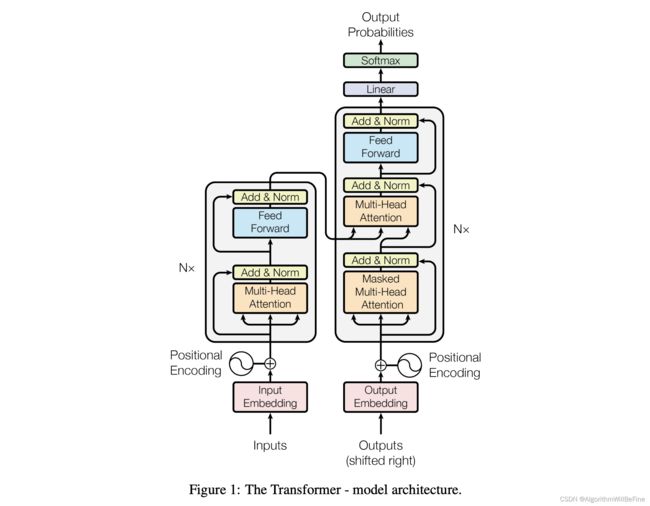
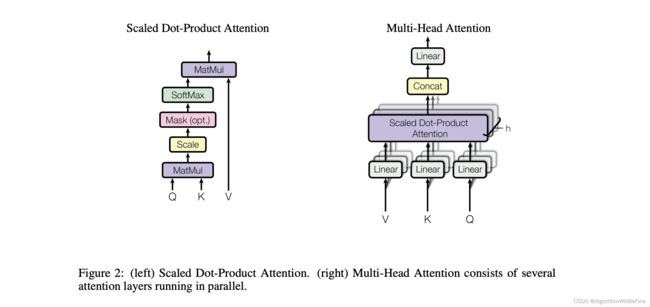
手撕transformer-基于numpy实现

Attention is all you need

在Transformer模型中，输入首先通过一个嵌入层，得到每个词的嵌入表示，然后再加上位置编码（Positional Encoding）得到每个词的最终表示。得到这个最终表示后，为了计算注意力权重，我们需要为每个输入生成 Q (Query), K (Key), 和 V (Value)。

具体的转换过程如下：

1. 词嵌入: 首先，我们有一个嵌入矩阵，其大小为 (vocab_size, d_model)，其中 vocab_size 是词汇表的大小，d_model 是模型的维度。输入句子中的每个词都会通过查找这个嵌入矩阵得到其嵌入表示。

   embeddings = embedding_matrix[input_sentence]
   

2. 位置编码: 之后，我们会加上位置编码。这一步是为了给模型提供词的位置信息，因为Transformer模型本身没有关于位置的固有概念。

   embeddings += positional_encoding
   

3. 生成 Q, K, 和 V: 接下来，我们将嵌入结果（词嵌入+位置编码）传递给三个不同的全连接层（dense layers），分别得到 Q, K 和 V。

   Q = np.dot(embeddings, WQ)
   K = np.dot(embeddings, WK)
   V = np.dot(embeddings, WV)
   

   这里的 WQ, WK, 和 WV 是三个权重矩阵，它们是模型需要学习的参数。

简而言之，输入首先被转换为嵌入表示，然后加上位置编码，最后通过三个不同的全连接层得到 Q, K 和 V。

Scaled Dot-Product Attention

import numpy as np

def scaled_dot_product_attention(q, k, v, mask=None):
   matmul_qk = np.dot(q, k.T)
   d_k = k.shape[-1]
   scaled_attention_logits = matmul_qk / np.sqrt(d_k)

   if mask is not None:
       scaled_attention_logits += (mask * -1e9)

   attention_weights = np.exp(scaled_attention_logits) / np.sum(np.exp(scaled_attention_logits), axis=-1, keepdims=True)
   output = np.dot(attention_weights, v)
   return output, attention_weights

# 测试
d_k = 3
batch_size = 1

# Query: 我们要查询的内容，这里假设是一个批次中的两个句子，每个句子有3个词，每个词的嵌入维度是3。
q = np.array([[1, 0, 1], [0, 2, 0], [1, 1, 0]]) 

# Key: 我们要匹配的内容
k = np.array([[1, 1, 0], [0, 1, 1], [1, 0, 1]])

# Value: 当我们找到与Query匹配的Key时，我们希望返回的实际内容。
v = np.array([[0, 2, 0], [0, 3, 0], [1, 0, 2]])

output, attention_weights = scaled_dot_product_attention(q, k, v)
print("Output:", output)
print("Attention Weights:", attention_weights)

Multi-head Attention

Multi-head Attention 是 Transformer 模型中的关键组件。它的核心思想是：不仅可以在一个子空间（或“头”）中捕获注意力模式，还可以同时在多个子空间中捕获多种不同的注意力模式。这使得模型能够更全面地理解数据。

每一个“头”都执行一次独立的注意力操作（Scaled Dot-Product Attention）。然后，所有头的输出会被串联起来，并通过一个线性变换。这样，多头注意力机制可以允许模型在不同的表示子空间中并行地关注不同的信息。

多头注意力的计算步骤如下：

1. 线性投影: 对于每一个头，我们都有自己的权重矩阵 (W_Q), (W_K), 和 (W_V)。输入 (X)（这可以是编码器的输入或前一个编码器/解码器的输出）会被线性投影为 Q, K, 和 V。

   $Q=X{W}_Q$
   $K=X{W}_K$
   $V=X{W}_V$

2. Scaled Dot-Product Attention: 对于每一个头，我们都使用 Q, K, 和 V 来执行一次独立的注意力操作。

3. 串联: 所有头的输出会被串联起来。

4. 线性变换: 串联后的输出会经过另一个线性变换，得到多头注意力的最终输出。

def multi_head_attention(num_heads, d_model, input):
    depth = d_model // num_heads
    WQ = np.random.randn(d_model, d_model)
    WK = np.random.randn(d_model, d_model)
    WV = np.random.randn(d_model, d_model)
    WO = np.random.randn(d_model, d_model)
    
    q = np.dot(input, WQ)
    k = np.dot(input, WK)
    v = np.dot(input, WV)
    
    # Splitting for multiple heads
    q = np.split(q, num_heads, axis=1)
    k = np.split(k, num_heads, axis=1)
    v = np.split(v, num_heads, axis=1)

    heads = []
    for i in range(num_heads):
        out, _ = scaled_dot_product_attention(q[i], k[i], v[i])
        heads.append(out)
    
    # Concatenating heads
    concat_heads = np.concatenate(heads, axis=1)
    
    # Final linear layer
    output = np.dot(concat_heads, WO)
    return output

# Test
input_data = np.random.randn(5, 64)  # 5 tokens with 64-d embeddings
output = multi_head_attention(8, 64, input_data)
print(output.shape)  # It should return (5, 64)

Position-wise Feed-Forward Networks

在 Transformer 中，除了注意力机制外，还有一个重要的组件，即位置逐点前馈网络（Position-wise Feed-Forward Networks）。这实际上是两个线性变换的序列，它们之间有一个 ReLU 激活函数。这些前馈网络独立地应用于每一个位置（每一个序列元素）。

结构可以描述为：
$$\text{FFN}(x)=\max (0,x{W}_1+b_1)W_2+b_2$$
其中：
$$x:输入$$ $$W_1,W_2:权重矩阵$$ $$b_1,b_2:是偏置项$$

def feed_forward_network(d_model, d_ff, x):
    # First linear layer
    W1 = np.random.randn(d_model, d_ff)
    b1 = np.random.randn(d_ff)
    
    # Second linear layer
    W2 = np.random.randn(d_ff, d_model)
    b2 = np.random.randn(d_model)

    # Feed forward network
    out = np.dot(x, W1) + b1
    out = np.maximum(0, out)  # ReLU activation
    out = np.dot(out, W2) + b2
    return out

# Test
input_data = np.random.randn(5, 512)  # 5 tokens with 512-d embeddings
d_model = 512
d_ff = 2048
output = feed_forward_network(d_model, d_ff, input_data)
print(output.shape)  # It should return (5, 512)

Layer Normalization

# Layer Normalization
def layer_norm(x, epsilon=1e-6):
    mean = np.mean(x, keepdims=True, axis=-1)
    std = np.std(x, keepdims=True, axis=-1)
    return (x - mean) / (std + epsilon)

Single Transformer Layer

根据以上实现的功能，我们可以构建一个Transformer层，它包含一个多头注意力层，一个前馈神经网络，以及两个残差连接

def transformer_encoder_layer(d_model, num_heads, x):
    # Multi-head Attention
    attn_output = multi_head_attention(num_heads, d_model, x)
    
    # Residual Connection + Layer Normalization
    x = layer_norm(x + attn_output)
    
    # Feed Forward Network
    ff_output = feed_forward_network(d_model, d_model * 4, x)
    
    # Residual Connection + Layer Normalization
    out = layer_norm(x + ff_output)
    return out

# Test
input_data = np.random.randn(10, 512)  # 10 tokens with 512-d embeddings
output = transformer_encoder_layer(512, 8, input_data)
print(output.shape)  # It should return (10, 512)

总结

1. 基本结构：

• Transformer 结构包括编码器（Encoder）和解码器（Decoder）部分。每部分都是多层的结构，即由多个重复的编码器层或解码器层组成。

2. 核心概念：

• 自注意力机制 (Self-Attention Mechanism): 这允许 Transformer 在输入序列的不同位置间计算其关联性，然后根据这些关联性进行加权组合。

• 多头注意力 (Multi-Head Attention): 而不是只计算一种注意力权重，Transformer 在多个子空间中并行地计算多组权重。这可以帮助模型捕捉各种不同的关系。

• 位置编码 (Positional Encoding): 由于 Transformer 本身不具有顺序感知能力，所以引入位置编码来给模型提供序列中词汇的位置信息。

3. 其他重要特点：

• 前馈全连接网络 (Feed Forward Neural Networks): 在每个 Transformer 层中，除了注意力机制外，还有一个位置全连接网络。

• 残差连接 (Residual Connections): 这有助于避免深度网络中的梯度消失问题。

• 层归一化 (Layer Normalization): 在每个子层（如多头注意力或前馈网络）后都有归一化操作。

4. 优势：

• 并行性: 与 RNN 和 LSTM 相比，Transformer 可以处理整个序列的所有单词/标记，而无需按顺序迭代它们，从而大大提高了计算效率。

• 捕获长距离依赖: 由于其自注意力机制，Transformer 可以轻松捕获序列中的长距离依赖关系。

5. 缺点:

当然，尽管 Transformer 架构在多种任务中取得了出色的表现，但它也有一些缺点和限制：

• 计算资源要求高：尤其是当处理长序列时，Transformer 的自注意力机制需要大量的计算资源。因为自注意力需要为序列中的每个词与其他每个词之间计算权重，这导致了 (O(n^2)) 的复杂性，其中 (n) 是序列长度。

• 需要大量的数据：为了充分利用 Transformer 的能力，通常需要大量的训练数据。在数据有限的场景下，Transformer 容易过拟合。

• 训练时间长：大型的 Transformer 模型（例如 GPT-3 或 T5）需要多天甚至数周的时间和特定的硬件加速（如 GPU 或 TPU）来进行训练。

• 模型大小：许多现代的 Transformer 变体（如 BERT, GPT-2, GPT-3）具有数十亿甚至数万亿的参数，这使得部署在资源有限的环境（如移动设备）变得困难。