2023年第五届传智杯前四题题解(后俩没写出来)
比赛链接:第五届“传智杯”全国大学生计算机大赛(决赛B组) - 比赛详情 - 洛谷
时效「月岩笠的诅咒」
题目背景
蓬莱之药,被诅咒的不死之药。
奉命将蓬莱之药投入富士山中销毁的月岩笠,最终打算把蓬莱之药改投入八岳销毁。在下山途中妹红将其踹下山,抢到了蓬莱之药。
那已经是千年前的事情了。
题目描述
时间节点上发生过的两件事情的时间可被看作两实数 a,b。我们称两个事件满足「周年」关系,当且仅当可以通过执行以下两种操作(可以 00 次)使其相等:
- 将 a 加上 11,即 a←a+1;
- 将 b 加上 11,即 b←b+1。
现在给定实数 a,b,询问它们是否满足「周年」。
输入输出样例
输入 #1 100.000000000000 999999.000000000000
输出 #1 YES
输入 #2 114.123456789000 514.123456789000
输出 #2 YES
输入 #3 0.333333333333 0.333333333334
输出 #3 NO
说明/提示
对于全部数据,保证 0 解析: 第一道题目只是告诉了我们这个数字可以进行+1和-1,但是对于小数的部分他完全不操作,对于这道题目的任何两个数字,只要小数相同,那么整数部分一定可以通过操作相同,所以这道题目的本质就是对小数部分进行判重,相同输出YES,不同输出NO即可; 藤原氏,权倾一时的重臣。凭借着炙手可热的权势,杀害了政敌长屋王而触碰到了最高的权力。 是天谴吗?即使修缮寺庙积德行善,藤原四兄弟最终覆灭在了天花之下。 环环相扣的因果报应可看成平面上的 �n 个小正方形,它们的边长分别为 1,2,3,⋯ ,�1,2,3,⋯,n。初始时,编号较小的正方形被编号较大的正方形完全包含: 为了方便记录正方形的位置,我们取正方形左上角的坐标 (xi,yi) 为正方形的坐标。此时可以唯一确定该正方形。 现在需要将最小的正方形的位置移动到 (xend,yend),移动过程满足: 请求出最少次数。 第一行有三个整数 n,xend,yend,含义如题面所示。 接下来 n 行,每行有两个整数xi,yi,描述第 i 小的正方形左上角的坐标。 输出共一行一个整数,表示最小的操作步数。 输入 #1 输出 #1 3 输入 #2 输出 #2 24 对于全部数据,1≤n≤105,0≤xi,yi,xend,yend≤109。 首先我们发现这道题目的数据量高达1e5,说明双重循环肯定是过不掉的,所以我们应该聪明的想:肯定有一次循环就可过掉的方法; 那么经过我们的观察发现,无论我们怎么移动,最后我们的最小框肯定是要和最后位置重叠的,那么除了最小框以外,其他的所有框应该满足,他也得框住最后的答案,因为我们始终要满足小框在大框以内这个条件。 基于此我们就可以进行贪心写法,每一次我们只保证把这个框框住答案,至于他是哪一步框住的我们可以不用考虑,因为我们最后的答案保证了这个移动的唯一性,也就是所有框的移动顺序不是唯一的,但是最短的结果唯一,这样我们也就解决了双重循环的问题; 代码中我们首先应该计算出我们大框的上下左右四个坐标位置,同时我们的结果位置也要计算出上下左右四个位置,与大框的位置一一对应才能保证他被框住。 具体判断大家可以自行画图。 代码如下: 徐福是秦朝齐地方士。 奉秦皇之命,徐福率三千童男童女踏上了寻找传说中的「蓬莱之药」的征途。但最后再也没有回来。 徐福最终去了哪里?有没有找到蓬莱之药?这些问题已经无关紧要了。 时间的流逝可以抽象成对数字序列进行排序所花费的时间。不同排序策略花费的时间是不同的。这里介绍一种人类探索排序过程中具有里程碑意义的一种排序算法:希尔排序。 希尔排序可以被视为一种对插入排序的优化。为了研究希尔排序的运行效率,我们希望你实现一个简单的希尔排序的过程。在这之前,我们会规范插入排序的具体流程以及评价一个插入排序的过程的「代价」。 对于一个长度为 n 的数组 a=[a1,a2,⋯,an],插入排序的思想是,从前到后枚举每一个元素,将其插入到正确的位置上去: 如图所示是一个典型的插入排序的过程。在第 i 轮中我们把下标为 i 的元素插入到了排好序的部分中第一个比 ai 大的元素之前。假设 ai 最终被插入到了 bi 位置,那么我们称这一轮的代价为 ∣ai−bi∣+1,整个插入排序的过程的代价就是每一轮的代价之和。 为了减小插入排序的代价,我们引入了希尔排序。希尔排序将整个排序过程分成了若干轮,每一轮会按照一定的间隔把元素分组,对每一组内的元素分别进行排序。在最后一轮,希尔排序会对整个数组进行一次最终的插入排序。 具体的分组方式是,选定一个整数 d,划分为如下组别: 下面是一轮希尔排序的过程。我们选定 d=3。 希尔排序每一轮分别选取 d,并且在最后一轮取 d=1,每一轮都进行这样的排序,最终得到一个有序的数组。 虽然看上去进行了很多轮插入排序,但是最终每一轮插入排序的代价之和可能会远小于对整个数组进行单次插入排序的代价(上述例子中体现得并不明显,可以参考样例 2,32,3 给出的例子)。 事实上,希尔排序是人类发现的第一个最坏复杂度低于 Θ(n2) 的排序算法。例如,当取 d=2k−1, k=⌊log2n⌋,⌊log2n⌋−1,⌊log2n⌋−2,⋯,1 时,整个过程的最坏时间复杂度为 Θ(n3/2)。 第一行有两个整数 n,m,分别表示待排序的数组的长度以及希尔排序进行的轮数。 第二行有 n 个整数 a1,a2,⋯,an,描述数组里的元素。 第三行有 m 个整数 d1,d2,⋯,dm,描述每一轮选取的 d 的值。数据保证 dm=1。 第一行输出一个整数 costcost,表示整个希尔排序过程中插入排序产生的代价之和。 第二行输出 n 个整数,表示数组 a 排序后的结果。 输入 #1 输出 #1 输入 #2 输出 #2 输入 #3 输出 #3 对于全部数据,保证 1≤n≤105,1≤m≤100,cost≤5×107cost≤5×107,1≤ai≤109,1≤di≤n,dm=1。 首先这道题目的难度是要高于第四题的,但是在题目顺序上他却把这道题目放在了第四题之前(我是不知道为什么,但是隐约猜到了) 这道题目的数据范围在1e5,按道理来说最坏的情况是n方其实你是过不去的,但是可能是出题人数据太水或者是怎么滴,反正这道题你直接暴力的确是可以过掉的。 这也是为什么考场上好多人先看到了这个题目,结果却跳过了先做出了第四道的原因吧。 具体方法是:直接模拟题目给我们的过程。 首先:根据最后输入的m个整数,每次对其进行希尔排序,这里不用考虑dm序列的正确性,因为最后一个必定是1,也就是希尔排序在最后肯定进行一次完全的插入排序,保证了最后的序列一定是有序的; 接着找到根据dm,每次选取序列中想个dm个位置的数字进行插排,这里为了简化过程,我开了额外的空间存储之后再进行排序,最后按顺序在插入原序列即可; 进行第二步插排的时候记得用一个变量记录交换次数,最后还要输出呢; 代码如下: 正直的人,坚强不屈的人,刚正不阿的人。 大约这样的人会处处吃亏吧,不过这样的观点大约是从欺骗者的眼光里看到的。正直的人,即使是在死后,也是最为人尊敬的吧。 有一台计算器,使用 k 位的带符号整型来对数字进行存储。也就是说,一个变量能够表示的范围是[- 由于奇怪的特性,如果两个变量在相加时得到的结果在[−2k−1,2k−1) 之外,即发生了溢出,那么这台计算器就会卡死,再也无法进行计算了。 为了防止这样的事情发生,一个变通的方法是更改 ai 的排列顺序。容易发现这样不会改变计算出的和的值。 不过,可能不存在一种方案,使得计算出这 n 个数并且计算机不爆炸。但我们还是希望,计算出尽量多的数字的和。 第一行有两个整数 n,k,分别表示元素个数和整型位数。 第二行有 n 个整数a1,a2,⋯,an。 共一行一个整数,表示最多能将多少个数字计算出和。 输入 #1 输出 #1 输入 #2 输出 #2 对于全部数据,保证 1≤n≤500,1 首先我们发现,这个序列有正负数,而且要求你相加不超过指定范围,说明肯定存在某种最优序列,保证你每加一次这个数都应该在范围内波动,而且是最优。 其实我们很容易想到应该把正负数分开,每次只取最小的进行相加,直到加到双方都不能再加的时候即可停止,这里的双方都不能再加的意思是,加一个整数就会超范围,加负数也会超范围,或者没有正数没有负数之类的情况,我们可以用两个变量记录一下进行; 切记他会出现某一方加不了,而另一方能加的情况,此时绝对不要标记某一方为不能加,因为可能出现连续加了一方后,另一方又能加的情况, 第五题没写出来,写了一半了,最后一步贪心出错了; 基本方法就是,首先通过find函数找到每一层有多少个点,我这里猜测的是,我们需要从头遍历到尾,每一次只取递增序列,并且如果后面小于前面可以直接直接加上前面的数,这样的写法最后是错误的,只过了各点,具体的正确方法我还没找到。代码也就不给大家看了; 总结:这次比赛三个小时,第一题差点首A,我估计我是第二个交的,因为提前发了试卷,我写出来之后题目一开放我就交了,我后来翻排名发现有个人和我一样时间用了00.00,但他是首a我不是,所以我猜测就差了一两秒就首a了,有点可惜, 写了四道题花费两个半小时,写完四道题后我的排名在前,看了半个小时榜单,掉到了后面,不过按照一千人的底数我仍然能够国奖,还是挺幸运的; 省赛的话只写了两道题还是三道题,卡在了省二的边缘没进,要不是官方大发慈悲给了省二罚时多调了一万的基数我当时就省三进不了决赛了。 说明国赛来的人还是挺少的,让我给混了一个国奖,如果底数足够大的话,我应该能国一,也算是一个很好的奖了 至此结束#include
题目背景
题目描述
输入格式
输出格式
输入输出样例
3 2 1
1 0
1 0
0 1
15 8 4
9 0
9 1
9 1
8 1
8 2
8 3
7 3
6 3
5 3
4 3
3 3
2 4
2 5
1 6
0 7
说明/提示
样例 1 解释
数据范围及约定
#include
题目背景
题目描述
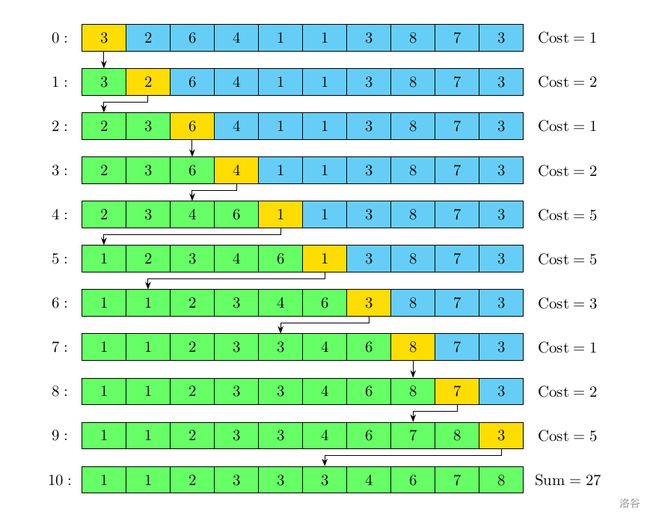
插入排序
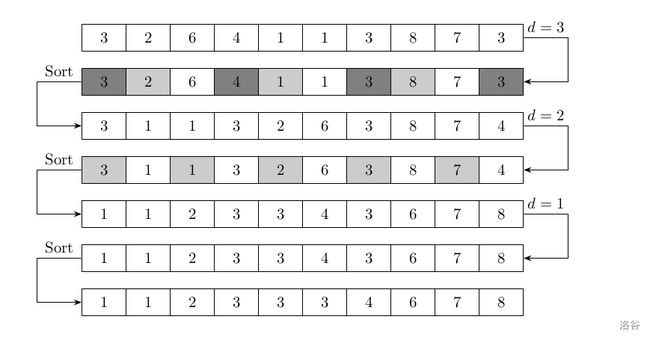
希尔排序
输入格式
输出格式
输入输出样例
10 1
3 2 6 4 1 1 3 8 7 3
1
27
1 1 2 3 3 3 4 6 7 8
15 1
15 14 13 12 10 11 9 8 7 4 5 6 3 2 1
1
116
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
15 3
15 14 13 12 10 11 9 8 7 4 5 6 3 2 1
9 3 1
68
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
说明/提示
数据范围及约定
#include
题目背景
题目描述
![]() ,
,![]() )。现在我们希望使用该计算器计算一系列数 a1,a2,⋯,an 的和。计算的伪代码如下:
)。现在我们希望使用该计算器计算一系列数 a1,a2,⋯,an 的和。计算的伪代码如下:输入格式
输出格式
输入输出样例
3 3
1 2 3
2
10 4
-3 5 6 -4 5 3 -4 1 -1 0
9
说明/提示
样例解释
数据范围及约定
#include