算法基础课

acwing算法基础课

---

(一) 基础算法

快速排序

题目描述
给定你一个长度为 n 的整数数列。
请你使用快速排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行，第一行包含整数 n。
第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整个数列。
输出格式
输出共一行，包含 n 个整数，表示排好序的数列。
输入样例：
5
3 1 2 4 5
输出样例：
1 2 3 4 5

代码如下：

#include 
#include 
#include 
using namespace std;
const int N = 1e5+10;
void quick_sort(int q[],int l,int r)
{
    if(l>=r) return;
    int i=l-1,j=r+1,x=q[l+r>>1];
    while(i<j)
    {
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i<j) swap(q[i],q[j]);
    }
    quick_sort(q,l,j);
    quick_sort(q,j+1,r);
}
int main()
{
    int n;
    int q[N];
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
        scanf("%d", &q[i]);
    }
    quick_sort(q,0,n-1);
    for(int i=0;i<n;i++)
    {
        cout<<q[i]<<" ";
    }
    return 0;
}

---

快速选择

给定一个长度为 n 的整数数列，以及一个整数 k，请用快速选择算法求出数列从小到大排序后的第 k 个数。
输入格式
第一行包含两个整数 n 和 k。
第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整数数列。
输出格式
输出一个整数，表示数列的第 k 小数。
数据范围
1≤n≤100000,
1≤k≤n
输入样例：
5 3
2 4 1 5 3
输出样例：
3

代码如下：

const int N = 1e5+10;
int a[N];
int quick_sort(int l,int r,int k)
{
    if(l>=r) return a[k];
    int i=l-1,j=r+1,x=a[l+r>>1];
    while(i<j)
    {
        do i++;while(a[i]<x);
        do j--;while(a[j]>x);
        if(i<j) swap(a[i],a[j]);
    }
    if(k<=j) return quick_sort(l,j,k);
    else return quick_sort(j+1,r,k);
}
int main()
{
   int n,k;
   cin>>n>>k;
   for(int i=0;i<n;i++)
   cin>>a[i];
   cout<<quick_sort(0,n-1,k-1);
   return 0;
}

---

归并排序

题目描述
给定你一个长度为 n 的整数数列。
请你使用归并排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行，第一行包含整数 n。
第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整个数列。
输出格式
输出共一行，包含 n 个整数，表示排好序的数列。
数据范围
1≤n≤100000
输入样例：
5
3 1 2 4 5
输出样例：
1 2 3 4 5

代码如下：

#include 
#include 
#include 
using namespace std;
const int N = 100010;
int n;
int q[N],tem[N];
void merge_sort(int q[], int l, int r)  // 归并排序
{
    if(l>=r) return;
    int mid=(l+r)/2;
    merge_sort(q,l,mid);merge_sort(q,mid+1,r);
    int k=0,i=l,j=mid+1;
    while(i<=mid&&j<=r)
    {
        if(q[i]<=q[j]) tem[k++]=q[i++];
        else tem[k++]=q[j++];
    }
    while(i<=mid) tem[k++]=q[i++];
    while(j<=r) tem[k++]=q[j++];
    for(i=l,j=0;i<=r;i++,j++) q[i]=tem[j];
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> q[i];
    merge_sort(q,0,n-1);
    for (int i = 0; i < n; i ++ ) cout << q[i]<<" ";
}

---

逆序对数量

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。
逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 ia[j]，则其为一个逆序对；否则不是。
输入格式
第一行包含整数 n，表示数列的长度。
第二行包含 n 个整数，表示整个数列。
输出格式
输出一个整数，表示逆序对的个数。
数据范围
1≤n≤100000 ，
数列中的元素的取值范围 [1,1e9]。
输入样例：
6
2 3 4 5 6 1
输出样例：
5

代码如下：

#include 
#include 
#include 
using namespace std;
const int N = 100010;
typedef long long LL;
int q[N],tmp[N];
LL merge_sort(int l,int r)
{
    if(l>=r) return 0;
    int mid=l+r>>1;
    LL ans=merge_sort(l,mid)+merge_sort(mid+1,r);
    int k=0,i=l,j=mid+1;
    while(i<=mid&&j<=r)
    {
        if(q[i]<=q[j]) tmp[k++]=q[i++];
        else 
        {
            tmp[k++]=q[j++];
            ans+=mid-i+1;
        }
    }
    while(i<=mid) tmp[k++]=q[i++];
    while(j<=r) tmp[k++]=q[j++];
    for(int i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];
    return ans;
}

int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> q[i];
    cout<<merge_sort(0,n-1);
   
}

---

二分法

---

数的范围

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式
第一行包含整数 n 和 q，表示数组长度和询问个数。

第二行包含 n 个整数（均在 1∼10000 范围内），表示完整数组。

接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式
共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例：
6 3
1 2 2 3 3 4
3
4
5
输出样例：
3 4
5 5
-1 -1

代码如下：

#include 
#include 
#include 
using namespace std;
const int N = 100010;
int q[N];
int SL(int l,int r,int x) //查找左边界
{
    while(l<r)
    {
        int mid=l+r>>1;
        if(q[mid]>=x) r=mid;
        else l=mid+1;
    }
    return l;
}
int SR(int l,int r,int x) //查找右边界
{
    while(l<r)
    {
        int mid=l+r+1>>1;
        if(q[mid]<=x) l=mid;
        else r=mid-1;
    }
    return r;
}
int main()
{
    int n,m;
    cin >> n>>m;
    for (int i = 0; i < n; i ++ )
    cin >> q[i];
    while (m -- )
    {
        int x;
        cin >> x;
        int l=SL(0,n-1,x); //查找左边界，并返回l
        if(q[l]!=x) cout << "-1 -1"<<endl;
        else 
        {
            cout << l<<" "; //找到了，就输出左下标
            cout << SR(0,n-1,x)<<endl; //输出右下标
        }
    }
    return 0;
}

例题中要用两次查找，因为要查找两个数，查找左边界和右边界

---

数的三次方根

给定一个浮点数 n，求它的三次方根。

输入格式
共一行，包含一个浮点数 n。

输出格式
共一行，包含一个浮点数，表示问题的解。

注意，结果保留 6 位小数。

数据范围
−10000≤n≤10000
输入样例：
1000.00
输出样例：
10.000000

#include 
#include 
#include 
using namespace std;
double x;
int main()
{
    double l=-10000,r=1e4;
    cin >> x;
    while(r-l>1e-8)
    {
        double mid=(l+r)/2;
        if(mid*mid*mid>=x) r=mid;
        else l=mid;//浮点数不用处理边界问题，即不用加一
    }
    printf("%lf",l);
    return 0;
}

---

四平方和

四平方和定理，又称为拉格朗日定理：

每个正整数都可以表示为至多 4 个正整数的平方和。

如果把 0 包括进去，就正好可以表示为 4 个数的平方和。

比如：

5=0²+0²+1²+2²
7=1²+1²+1²+2²
对于一个给定的正整数，可能存在多种平方和的表示法。

要求你对 4 个数排序：

0≤a≤b≤c≤d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列，最后输出第一个表示法。

输入格式
输入一个正整数 N。

输出格式
输出4个非负整数，按从小到大排序，中间用空格分开。

数据范围
06
输入样例：
5
输出样例：
0 0 1 2

二分做法

#include 
#include 
#include 
using namespace std;
const int N=5*1e6;
struct sum
{
    int s,c,d; //s是c*c+d*d
    bool operator <(const sum &t) //重载运算符，sort的时候按这个顺序排
    {
        if(s!=t.s) return s<t.s; //先看和，按从小到大
        if(c!=t.c) return c<t.c; //如果和相等，再看c的值
        return d<t.d; // 前两项都相等就根据d排序
    }
} s[N];
int main()
{
	int n,m=0;
	cin>>n;
	for(int c=0;c*c<=n;c++)
	 for(int d=c;d*d+c*c<=n;d++)
	   {
	   	s[m++]={c*c+d*d,c,d}; // 把枚举的每一组都存起来
	   }
	   sort(s,s+m);
	for(int a=0;a*a<=n;a++)
	 for(int b=a;b*b+a*a<=n;b++)
	    {
	    int t=n-a*a-b*b; // 要用二分法查找的值
		int l=0,r=m-1;
		while(l<r)
		{
		    int mid=l+r>>1;
		  if(s[mid].s>=t) r=mid;
		  else l=mid+1;	
	    } 	
	    if(s[l].s==t) //说明查找到想找的值了
	    {
	    cout<<a<<" "<<b<<" "<<s[l].c<<" "<<s[l].d<<endl;
	    return 0;
		}
		}   
		return 0;
}

这道题主要难点是要按字典序排列abcd，并且直接暴力会超时，所以转化成二重循环加二重循环，先枚举出c和d的每种结果（不能先枚举a和b，二分出的是小的值），再用哈希表或是二分法进行查找。运算符的重载。
暴力的做法

#include 
using namespace std;
int main()
{
  int a,b,c,d,n;
  cin>>n;
  for(a=0;a*a<=n;a++)
  {
    for(b=a;a*a+b*b<=n;b++)
    {
      for(c=b;a*a+b*b+c*c<=n;c++)
      {
       int t=n-a*a-b*b-c*c;
       for(d=c;d*d<=t;d++)
        if(d*d==t) {cout<<a<<" "<<b<<" "<<c<<" "<<d;return 0;}
      }
    }
  }
  return 0;
}

正好卡着过

---

分巧克力

儿童节那天有 K 位小朋友到小明家做客。

小明拿出了珍藏的巧克力招待小朋友们。

小明一共有 N 块巧克力，其中第 i 块是 Hi×Wi 的方格组成的长方形。

为了公平起见，小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。

切出的巧克力需要满足：

形状是正方形，边长是整数
大小相同
例如一块 6×5 的巧克力可以切出 6 块 2×2 的巧克力或者 2 块 3×3 的巧克力。

当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

输入格式
第一行包含两个整数 N 和 K。

以下 N 行每行包含两个整数 Hi 和 Wi。

输入保证每位小朋友至少能获得一块 1×1 的巧克力。

输出格式
输出切出的正方形巧克力最大可能的边长。

数据范围
1≤N,K≤1e5,
1≤Hi,Wi≤1e5
输入样例：
2 10
6 5
5 6
输出样例：
2

#include 
#include 
#include 
using namespace std;
const int N = 100010;
int h[N],w[N]; //定义长宽
int n,k;
bool check(int mid)
{
    int res=0; //记录巧克力数量
    for (int i = 0; i < n; i ++ )
    {
        res+=(h[i]/mid)*(w[i]/mid);  每一大块可以分成的边长为 mid 的巧克力数量
    }
    if(res>=k) return true;
    else return false;
}
int main()
{
    cin >> n>> k;
    for (int i = 0; i < n; i ++ ) cin >> h[i]>> w[i];
    int l=1,r=1e5; //巧克力边长的边界是1~1e5
    while(l<r)
    {
        int mid=l+r+1>>1;
        if(check(mid)) l=mid; //分情况讨论
        else r=mid-1;
    }
    cout << l; //l和r相等
}

长除以a代表可以有几列a,宽除以a可以代表有几行a
比如6X5的矩阵 a=3 ，6/3=2 5/3=1 代表最多有21=2个33的矩阵。

---

高精度

高精度加法

#include 
#include 
using namespace std;
vector<int> add(vector<int> &A,vector<int> &B)
{
    int t=0; //进位数
    vector<int> C;
    for(int i=0;i<A.size()||i<B.size();i++)
    {
        if(i<A.size()) t+=A[i]; 
        if(i<B.size()) t+=B[i];//加上两个数的第i位
        C.push_back(t%10); //将余数放在结果的第i位
        t/=10; //得出进位数
    }
    if(t) C.push_back(t); //如果最后t还有进位
    return C;
}
int main()
{
    string a,b; //以字符串形式保存
    vector<int> A,B;//保存两个整数的数组
    cin >> a>>b;
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
    auto C=add(A,B); //电脑自动识别类型（auto）
    for(int i=C.size()-1;i>=0;i--) cout << C[i];
    return 0;
}

主要思想就是分别在两个数组逆序存储两个整数，之后每位相加进位，不要漏了最后的最高位

---

高精度减法

给定两个正整数（不含前导 0），计算它们的差，计算结果可能为负数。

输入格式
共两行，每行包含一个整数。

输出格式
共一行，包含所求的差。

数据范围
1≤整数长度≤105
输入样例：
32
11
输出样例：
21

#include 
#include 
#include 
#include 
using namespace std;
vector<int> A,B,C;
bool cmp(vector<int>&A,vector<int>&B )
{
	//先比较位数
	if(A.size()!=B.size()) return A.size()>B.size();
	//从最高位开始比较 (两数位数相等) 
	for(int i=A.size()-1;i>=0;i--)
	{
		if(A[i]!=B[i]) return A[i]>B[i];
	 } 
	 //如果两数完全相等 
	 return true;
}
vector<int> sub(vector<int> &A,vector<int> &B)
{
	int t=0;
	for(int i=0;i<A.size();i++) //这里a一定长于或等于b的位数，只遍历a就行 
	{ //t=A[i]-B[i]-t 
		t=A[i]-t;
		if(i<B.size())  //判断b的位数是否合法
        t=t-B[i];
        C.push_back((t+10)%10);
         // 这里如果没有借位，(t + 10) % 10就刚好等于t
        // 如果这里有借位，(t + 10) % 10就会借一个10下来
        if(t<0) t=1;//如果t < 0，说明不够减，需要借位，把t赋值为1，就是在下一次执行中，A的当前位会减掉t
		else t=0; 
	}
	while(C.size()>1&&C.back()==0) C.pop_back(); //删除前导0
	return C; 
}
int main()
{
    string a,b;
    cin>>a>>b;
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
	for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
	//判断a和b的大小
	if(cmp(A,B)) //如果a>b 
	{
		C=sub(A,B);
		for(int i=C.size()-1;i>=0;i--) cout<<C[i];
	 } 
	 else //否则就调转a和b
	 {
	 	C=sub(B,A);
	 	cout<<"-";
	 	for(int i=C.size()-1;i>=0;i--) cout<<C[i];
	 }
	 return 0;
}
 

---

前缀和

---

一维前缀和

输入一个长度为 n 的整数序列。

接下来再输入 m 个询问，每个询问输入一对 l,r。

对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式
共 m 行，每行输出一个询问的结果。

数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例：
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例：
3
6
10

#include 
#include 
#include 
using namespace std;
const int N = 100010;
int a[N],sum[N]; 
int main()
{
    int n,m;
    cin >> n>>m;
    for (int i = 1; i <= n; i ++ )
        cin >> a[i];
        for (int i = 1; i <= n; i ++ ) sum[i]=sum[i-1]+a[i];
    while (m -- )
    {
        int l,r;
        cin >> l>>r;
        cout<<sum[r]-sum[l-1]<<endl;
    }  }

sum[r] = a[1] + a[2] + a[3] + a[l-1] + a[l] + a[l+1] … a[r];
sum[l - 1] = a[1] + a[2] + a[3] + a[l - 1];
sum[r] - sum[l - 1] = a[l] + a[l + 1]+…+ a[r]
前缀和sum【i】=sum【i-1】+a[i]

---

二维前缀和

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式
共 q 行，每行输出一个询问的结果。

数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17
27
21

#include 
#include 
#include 
using namespace std;
const int N = 1010;
int a[N][N],sum[N][N];
 int n,m,q;
int main()
{
    scanf("%d%d%d", &n,&m,&q);
    for (int i = 1; i <= n; i ++ )
    for (int j = 1; j <= m; j ++ )
    {
    cin >> a[i][j];
     sum[i][j]=sum[i-1][j]+sum[i][j-1]+a[i][j]-sum[i-1][j-1]; //预处理前缀和
    }
   //查询
    while(q--)
    {
        int x1,x2,y1,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
         printf("%d\n",sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]);
    }
    return 0;
}

1.二维前缀和预处理公式

s[ i ] [ j ] = s[ i-1 ][ j ] + s[ i ][ j-1 ] + a[ i ][ j ] - s[ i-1 ][ j-1 ]
2.以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]
（记住减一的都是x1，y1）

---

差分（前缀和逆运算）

---

一维差分

输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式
共一行，包含 n 个整数，表示最终序列。

数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例：
3 4 5 3 4 2

#include 
#include 
#include 
using namespace std;
const int N = 1e5+10;
int a[N],b[N]; //前缀和数组和差分数组（相当于s和a）
int main()
{
    ios::sync_with_stdio(false);
    int n,m;
    cin >> n>>m;
    for (int i = 1; i <= n; i ++ )
    {
        cin >> a[i];
        b[i]=a[i]-a[i-1];  //1.构建差分数组
    }
    while (m -- )
    {
        int l,r,c;
        cin >> l>>r>>c;
        b[l]+=c;     //2.改变差分数组的值，从而改变前缀和数组
        b[r+1]-=c;
    }
    for (int i = 1; i <= n; i ++ ) {a[i]=b[i]+a[i-1]; //3.更新前缀和数组
    cout << a[i]<<" ";}
    return 0;
}

差分里面是a数组是前缀和数组，b数组是差分数组。
如何构造差分b数组？

最为直接的方法

如下：

a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
b[3] =a [3] - a[2];
…
b[n] = a[n] - a[n-1];
也由此得出后面求前缀和数组是a【n】=b【n】+a【n-1】。
如何实现前缀和数组+c操作？

首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c, a[n] + c;

然后我们打个补丁b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,a[n] - c;

a【r】右边正好一加一减抵消。

---

二维差分

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2

#include 
#include 
#include 
using namespace std;
const int N = 1010;
int s[N][N],a[N][N]; //前缀和数组和差分数组
int main()
{
    int n,m,q;
    cin >> n>>m>>q;
    for (int i = 1; i <= n; i ++ )
    for (int j = 1; j <= m; j ++ )
    cin >> s[i][j];
    //1.构建差分数组
    for (int i = 1; i <= n; i ++ )
    for (int j = 1; j <= m; j ++ )
    a[i][j]=s[i][j]+s[i-1][j-1]-s[i][j-1]-s[i-1][j];
    //2.改变差分数组的值
    while (q -- )
   {
       int x1,x2,y1,y2,c;
       cin >> x1>>y1>>x2>>y2>>c;
       a[x1][y1]+=c;
       a[x2+1][y2+1]+=c;
       a[x1][y2+1]-=c;
       a[x2+1][y1]-=c;    //x2，y2有加一，联想记忆二维
   }
   //3.更新前缀和数组
   for (int i = 1; i <= n; i ++ )
   {
    for (int j = 1; j <= m; j ++ )
    {
        s[i][j]=a[i][j]+s[i][j-1]+s[i-1][j]-s[i-1][j-1];
        cout << s[i][j]<<" ";
    }
     cout<<endl;
   }
    return 0;
}

类比一维

---

双指针算法

主旨是先列出暴力算法，然后根据二者单调性进行优化

---

最长连续不重复子序列

给定一个长度为 n 的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度。

输入格式
第一行包含整数 n。

第二行包含 n 个整数（均在 0∼105 范围内），表示整数序列。

输出格式
共一行，包含一个整数，表示最长的不包含重复的数的连续区间的长度。

数据范围
1≤n≤10⁵
输入样例：
5
1 2 2 3 5
输出样例：
3

#include 
#include 
#include 
using namespace std;
const int N = 1e5+10;
int s[N],a[N];   //s数组作用类似于桶排序中的计数数组
int main()
{
    int res=0;
    int n;
    cin>>n;
    for (int i = 0; i < n; i ++ ) cin >> a[i];
    for (int j = 0,i=0; j < n; j ++ ) //j指的是所求序列的终点
    {
        s[a[j]]++;  //j每次右移，计数数组加一
        while(s[a[j]]>1)  //说明序列中有重复的，要把i右移
        {
            s[a[i]]--;  //序列起点右移，序列减少一个数
            i++;
        }
        //当循环结束i，j所指序列无重复
        res=max(res,j-i+1);
    }
    cout << res;
}

其中i指所求序列的起点，j指所求序列的终点

---

---

数组元素的目标和

给定两个升序排序的有序数组 A 和 B，以及一个目标值 x。

数组下标从 0 开始。

请你求出满足 A[i]+B[j]=x 的数对 (i,j)。

数据保证有唯一解。

输入格式
第一行包含三个整数 n,m,x，分别表示 A 的长度，B 的长度以及目标值 x。

第二行包含 n 个整数，表示数组 A。

第三行包含 m 个整数，表示数组 B。

输出格式
共一行，包含两个整数 i 和 j。

数据范围
数组长度不超过 10⁵。
同一数组内元素各不相同。
1≤数组元素≤10⁹
输入样例：
4 5 6
1 2 4 7
3 4 6 8 9
输出样例：
1 1

#include 
#include 
#include 
using namespace std;
const int N = 1e5+10;
int a[N],b[N];  
int main()
{
    int n,m,x;
    cin >> n>>m>>x;
    for (int i = 0; i < n; i ++ ) cin >> a[i];
    for (int i = 0; i < m; i ++ ) cin >> b[i];
    for (int i = 0,j=m-1; i < n; i ++ )
    {
        while(j>=0&&a[i]+b[j]>x) j--; 
        if(a[i]+b[j]==x) 
        {
            cout << i<<" "<<j;
            break;
        }
    }
    return 0;
}

这道题中两数组是递增数组，因此单调性为i值变大，j就变小（和一定，一加数变大，另一个变小），所以第二个数组直接从尾开始扫

---

判断子序列

给定一个长度为 n 的整数序列 a1,a2,…,an 以及一个长度为 m 的整数序列 b1,b2,…,bm。

请你判断 a 序列是否为 b 序列的子序列。

子序列指序列的一部分项按原有次序排列而得的序列，例如序列 {a1,a3,a5} 是序列 {a1,a2,a3,a4,a5} 的一个子序列。

输入格式
第一行包含两个整数 n,m。

第二行包含 n 个整数，表示 a1,a2,…,an。

第三行包含 m 个整数，表示 b1,b2,…,bm。

输出格式
如果 a 序列是 b 序列的子序列，输出一行 Yes。

否则，输出 No。

数据范围
1≤n≤m≤10⁵,
−10⁹≤ai,bi≤10⁹
输入样例：
3 5
1 3 5
1 2 3 4 5
输出样例：
Yes

#include 
#include 
#include 
using namespace std;
const int N = 1e5+10;
int a[N],b[N];
int main()
{
    int n,m;
    int i,j;
    scanf("%d%d", &n, &m);
    for (i = 0; i < n; i ++ ) scanf("%d",&a[i]);
    for (i = 0; i < m; i ++ ) scanf("%d",&b[i]);
    for(i=0,j=0;i<m;i++)  //扫描b数组
    {
        if(j<n&&a[j]==b[i]) j++;  //a数组未到结尾且两数组对应数相等
    }
    if(j==n) cout << "Yes";  //说明a数组的数在b中都能找到对应
    else cout << "No";
    return 0;
}

这道题主旨就是b数组每次向后扫，a数组只有与其相等时才向后扫，最后看j和a数组长度n是否相等

---

离散化——区间和

假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。

现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c。

接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式
第一行包含两个整数 n 和 m。

接下来 n 行，每行包含两个整数 x 和 c。

再接下来 m 行，每行包含两个整数 l 和 r。

输出格式
共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围
−10⁹≤x≤10⁹,
1≤n,m≤10⁵,
−10⁹≤l≤r≤10⁹,
−10000≤c≤10000
输入样例：
3 3
1 2
3 6
7 5
1 3
4 6
7 8
输出样例：
8
0
5

#include 
#include 
#include 
using namespace std;
const int N=300010; //n次插入和m次查询相关数据量的上界(n+2m)
int n,m; 
int a[N],s[N]; //a数组存储对应坐标插入的值，s为a的前缀和数组
vector<int> alls; //存入所有插入和查询的坐标
vector<pair<int,int>> add,query; //存储插入和查询的数据
int find(int x)   //返回x的离散化坐标（+1是因为从一开始，好算前缀和）
{
    int l=0,r=alls.size()-1;
    while(l<r)
    {
        int mid=l+r>>1;
        if(alls[mid]>=x) r=mid;
        else l=mid+1;
    }
    return r+1;
}

int main()
{
	scanf("%d%d",&n,&m);
	//1.先进行各种数据的读入
	for(int i=0;i<n;i++)
	{
		int x,c;
		scanf("%d%d",&x,&c);
		alls.push_back(x); //存入插入坐标
		add.push_back({x,c});
	}
	for(int i=0;i<m;i++)
	{
	    int l,r;
	    scanf("%d%d", &l, &r);
	    query.push_back({l,r});
	    alls.push_back(l); //存入查询坐标
	    alls.push_back(r);
	}
	//2.对alls数组进行排序和去重操作
	sort(alls.begin(),alls.end());
	alls.erase(unique(alls.begin(),alls.end()),alls.end());
	//3.遍历add，对a数组进行插入操作
	for(auto it:add)
	{
	    int i=find(it.first); //返回离散化下标，即输入的下标对应的离散化下标
	    a[i]+=it.second;
	}
	//3.求前缀和
	for(int i=1;i<=alls.size();i++) s[i]=s[i-1]+a[i];
	//4.遍历query，进行查询操作
	for(auto it:query)
	{
	    int l=find(it.first);
	    int r=find(it.second);
	    cout << s[r]-s[l-1]<<endl;  //前缀和公式
	}
	return 0;
	
}

unique是去重函数，将重复的数放到数组最后，返回第一个重复数的下标

erase是删除函数，删去前一个和后一个之间的数，即正好删去重复数

当题目中所给数的值域大，但数的个数少时就使用离散化操作，即vector数组中存入所有需要的地址并去重排序，另开数组中按照原地址排序后的地址存储

alls数组中放所有地址是为了后序find函数中使用，无论是插入还是查询操作都要使用find函数来寻找离散化下标。
再强调一下：all中存的是待操作元素的坐标。比如all[100] = 10e5, 就代表着要操作的第100个元素的坐标为10e5, 因此all的元素长度其实是和操作的元素个数相关的, 也就是n+2m。

---

区间合并

给定 n 个区间 [li,ri]，要求合并所有有交集的区间。

注意如果在端点处相交，也算有交集。

输出合并完成后的区间个数。

例如：[1,3] 和 [2,6] 可以合并为一个区间 [1,6]。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含两个整数 l 和 r。

输出格式
共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围
1≤n≤100000,
−10⁹≤li≤ri≤10⁹
输入样例：
5
1 2
2 4
5 6
7 8
7 9
输出样例：
3

#include 
#include 
#include 
using namespace std;
typedef pair<int,int> PII;
vector<PII> seg;  //存放输入的区间（segment）
int merge(vector<PII>&seg)    //合并函数
{
    sort(seg.begin(),seg.end());   //先将seg排序（按左端点）
    int res=0;  //答案
    int l=-2e9,r=-2e9;   //定义超出数据范围的左右端点，方便后续更新和比较
    for(auto item:seg) //遍历数组
    {
        if(item.first>r)    //分三种情况讨论，这是第一种情况，两区间无法合并
        {
            if(l!=-2e9) res++;    //如果不是第一个区间，就答案加一
            l=item.first;     //新区间出现，每次更新左右区间界限
            r=item.second;
        }
        else r=max(r,item.second);   //包含第二三种情况，即部分在和全部在前一个划定好的区间
    }                                  //可以画图理解
        res++;    //可以举例看，比如只输入一个区间时会少算一个，其他的也一样，最后要把答案加一
    return res;
}
int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        int l,r;
        scanf("%d%d",&l,&r);
        seg.push_back({l,r});
    }
    int res=merge(seg);
    cout << res;
}

这个题思想就是先把存区间的数组按左端点排序（c++里默认按左边的数排序）；
然后按三种不同情况（完全在外面；部分在外面；全部在里面）选择更新左右端点或是只更新右端点

---

（二）数据结构

---

KMP

字符串s，模式串p，模式串 P 在字符串 S 中多次作为子串出现。

求出模式串 P 在字符串 S 中所有出现的位置的起始下标。
输入格式
第一行输入整数 N，表示字符串 P 的长度。

第二行输入字符串 P。

第三行输入整数 M，表示字符串 S 的长度。

第四行输入字符串 S。

输出格式
共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围
1≤N≤105
1≤M≤106
输入样例：
3
aba
5
ababa
输出样例：
0 2

#include 
using namespace std;
const int N=1e5+10,M=1e6+10;
char p[N],s[M];
int ne[N];//s是主串，p是子串
int n,m;
int main()
{
    cin>>n>>p+1>>m>>s+1; //下标均从一开始
    for(int i=2,j=0;i<=n;i++)
    { //i代表数组下标，j表示匹配成功的长度，i为一时ne为0，所以从二开始
        while(j&&p[i]!=p[j+1]) j=ne[j]; //匹配不成功
        if(p[i]==p[j+1]) j++; //匹配成功
        ne[i]=j;
    }
    for(int i=1,j=0;i<=m;i++)
    {
        while(j&&s[i]!=p[j+1]) j=ne[j]; //匹配不成功
        if(s[i]==p[j+1]) j++; //匹配成功
        if(j==n) //长度为n，匹配完成
        {
            cout<<i-j<<" ";
            j=ne[j]; //为了看后续是否还有能匹配的
        }
    }
    return 0;
}

背板子

---

并查集

合并集合

一共有 n 个数，编号是 1∼n，最开始每个数各自在一个集合中。

现在要进行 m 个操作，操作共有两种：

M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；
输入格式
第一行输入整数 n 和 m。

接下来 m 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式
对于每个询问指令 Q a b，都要输出一个结果，如果 a 和 b 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围
1≤n,m≤105
输入样例：
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例：
Yes
No
Yes

#include 
using namespace std;
const int N=1e5+10;
int p[N]; //定义多个集合
int find(int x) //用于返回祖宗节点
{
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) p[i]=i;
    while (m -- )
    { 
        char c;
        int a,b;
        cin>>c>>a>>b;
        if(c=='M') p[find(a)]=find(b);  //集合合并操作
        else if(find(a)==find(b)) cout<<"Yes"<<endl; //如果祖宗节点相同，说明在同一集合
        else cout<<"No"<<endl;
    }
    return 0;
}

---

连通块中点的数量

堆排序

输入一个长度为 n 的整数数列，从小到大输出前 m 小的数。

输入格式
第一行包含整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

输出格式
共一行，包含 m 个整数，表示整数数列中前 m 小的数。

数据范围
1≤m≤n≤105，
1≤数列中元素≤109
输入样例：
5 3
4 5 1 3 2
输出样例：
1 2 3

#include 
#include 
#include 
using namespace std;
const int N=1e5+10;
int a[N],n,m;
void adjust(int l,int r)   //筛选法调整函数
{ //函数前提是假设【l+1,r】已经是堆，插入了l
    int temp=a[l];  //暂存堆顶元素
    for(int i=2*l;i<=r;i*=2)    //遍历左右孩子
    {
        if(i+1<=r&&a[i]>a[i+1]) i++;   //如果右孩子存在且是二者中的小孩子，就指向右孩子
        if(temp<=a[i])  break;   //堆顶元素最小，不用比较了
        a[l]=a[i]; l=i;  //小孩子单项赋值给堆顶，指针指向小孩子，后续从小孩子左右孩子中继续比较
    }
    a[l]=temp;
}
int main()
{
    cin >> n>>m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    //建立小顶堆,从下到上调整
    for(int i=n/2;i>0;i--)
    {
        adjust(i,n);
    }
    int temp;
    for(int i=n;i>1;i--)
    {
        temp=a[1]; a[1]=a[i]; a[i]=temp; //把堆顶元素（最小）与最后一个交换
        adjust(1,i-1);   //最后一个已经归位，更新右边界
      
    }
    for(int i=n;i>n-m;i--)  //从最后一个向前输出m个数
    cout << a[i]<<" ";
}

---

单链表

实现一个单链表，链表初始为空，支持三种操作：

向链表头插入一个数；
删除第 k 个插入的数后面的数；
在第 k 个插入的数后插入一个数。
现在要对该链表进行 M 次操作，进行完所有操作后，从头到尾输出整个链表。

注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：

H x，表示向链表头插入一个数 x。
D k，表示删除第 k 个插入的数后面的数（当 k 为 0 时，表示删除头结点）。
I k x，表示在第 k 个插入的数后面插入一个数 x（此操作中 k 均大于 0）。
输出格式
共一行，将整个链表从头到尾输出。

数据范围
1≤M≤100000
所有操作保证合法。

输入样例：
10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6
输出样例：
6 4 6 5

总结：就是构建一个单链表，能实现头插，删除，插入，此处用数组来实现，比new更省时

#include 
#include 
#include 
using namespace std;
const int N = 1e5+10;
int head,idx,e[N],ne[N]; //表示头结点，下标索引(就是数组分配到哪个下标了)，存数据的数组，存指向下一个元素下标的数组
//这个head一开始指向头节点，为-1，这是不存在节点的情况下
//如果存在了节点，就将head的值换位头节点的下标，就从0开始一直到结束

void init()      
                 
{
    head=-1; //在后面进行不断操作后仍然可以知道链表是在什么时候结束
    idx=0;  //第一次插入从0开始，所以在后面主函数里k=0时进行一次head的特判
}
//插入第一个元素，head指向它
void add_to_head(int x)
{
    e[idx]=x;
    ne[idx]=head;
    head=idx;
    idx++;
}
//将x插入到下标为k的后面
void add(int k,int x)
{
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx;
    idx++;
}
//将下标为k的后面一个删去(其实没删，只是改变了指针的指向)
void remove(int k)
{
    ne[k]=ne[ne[k]]; //让k的指针指向，k的下下一个数
}
int main()
{
    init();
    int m;
    cin>>m;
    while (m -- )
    {
        char op;int x;int k;
        cin >> op;
        if(op=='H')
        {cin >>x;
         add_to_head(x);
        }
        else if(op=='I')
        {cin >> k>>x;
         add(k-1,x); //第k个插入的数下标为k-1
        }
        else if(op=='D')
        {cin >> k;
         if(k==0) head=ne[head]; //特判
         remove(k-1);
         
        }
    }
    for(int i=head;i!=-1;i=ne[i]) cout << e[i]<<" ";
    return 0;
}

头结点后面添加元素：

存储元素e[ide] = x;

该元素插入到头结点后面 ne[idx] = head; （head视为指针，指向原本的第一个元素）

头结点指向该元素 head = idx;

idx 指向下一个可存储元素的位置 idx++。

在索引 k 后插入一个数

存储元素e[idx] = x

该元素插入到第k个插入的数后面 ne[idx] = ne[k];

第k个插入的数指向该元素 ne[k] = idx;

idx 指向下一个可存储元素的位置 idx++。

---

哈希表

维护一个集合，支持如下几种操作：

I x，插入一个数 x；
Q x，询问数 x 是否在集合中出现过；
现在要进行 N 次操作，对于每个询问操作输出对应的结果。

输入格式
第一行包含整数 N，表示操作数量。

接下来 N 行，每行包含一个操作指令，操作指令为 I x，Q x 中的一种。

输出格式
对于每个询问指令 Q x，输出一个询问结果，如果 x 在集合中出现过，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围
1≤N≤10⁵
−10⁹≤x≤10⁹
1.拉链法（就是和单链表的梦幻联动）

#include 
#include 
#include 
using namespace std;
const int N = 1e5+3;  // 取大于1e5的第一个质数，取质数冲突的概率最小 可以百度
int h[N],e[N],ne[N],idx=0; //当做一排单链表理解，h存的就是每个链表的头结点 
void insert(int x)
{
    int k=(x%N+N)%N;  //除留余数法，找到下标，化为正数
    e[idx]=x;  //操作同单链表
    ne[idx]=h[k];  //h[k]就等于head
    h[k]=idx;
    idx++;
}
bool find(int x)
{
    int k=(x%N+N)%N;
    for(int i=h[k];i!=-1;i=ne[i])   //一个链表的最后一个的ne[i]是-1
    {
        if(e[i]==x) return 1;
    }
    return 0;
}
int main()
{
    memset(h,-1,sizeof(h));  //将槽先清空 空指针一般用 -1 来表示
    int n;
    cin >> n;
    while (n -- )
    {
        char c;int x;
        cin >> c>>x;
        if(c=='I')
        {
            insert(x);
        }
        else {
            if(find(x)) cout << "Yes"<<endl;
            else cout << "No"<<endl;
        }
    }
}

2.开放寻址法（线性探测再散列）

#include 
#include 
using namespace std;
const int N = 2e5+3; 一般会开成两倍的空间， 同时取下一个质数
const int null = 0x3f3f3f3f; //十六进制,比1e9更大
int h[N];
int find(int x)
{
    int k=(x%N+N)%N;
    while(h[k]!=null&&h[k]!=x)//这个坑有人
    {
        k++; //去下一个坑
        if(k==N) k=0; //到头了，从第一个坑开始找
    }
    return k; //k是x应该存的位置
}
int main()
{
    memset(h,0x3f,sizeof(h)); 
    int n;
    cin>>n;
    while (n -- )
    {
        char c[2];int x;
        scanf("%s%d",c,&x);
        int k=find(x);  //找到符合条件的位置
        if(*c=='I')
        h[k]=x;
        else {
            if(h[k]!=null) cout << "Yes"<<endl;
            else cout << "No"<<endl;
        }
    }
}

一个坑有人就去下一个坑

---

字符串哈希

给定一个长度为 n 的字符串，再给定 m 个询问，每个询问包含四个整数 l1,r1,l2,r2请你判断 [l1,r1] 和 [l2,r2]这两个区间所包含的字符串子串是否完全相同。

字符串中只包含大小写英文字母和数字。

输入格式

第一行包含整数 n和 m，表示字符串长度和询问次数。

第二行包含一个长度为 n的字符串，字符串中只包含大小写英文字母和数字。

接下来 m行，每行包含四个整数 l1,r1表示一次询问所涉及的两个区间。

注意，字符串的位置从 1开始编号。

输出格式

对于每个询问输出一个结果，如果两个字符串子串完全相同则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

1≤n,m≤10^5

输入样例：

8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
输出样例：

Yes
No
Yes

#include
#include
#include
using namespace std;
typedef unsigned long long ULL;
const int N = 1e5+5,P = 131;//131 13331
ULL h[N],p[N];

// h[i]前i个字符的hash值，p表示次方，第几个数是几次方
// 字符串变成一个p进制数字，体现了字符+顺序，需要确保不同的字符串对应不同的数字
// P = 131 或  13331 Q=2^64，在99%的情况下不会出现冲突
// 使用场景： 两个字符串的子串是否相同
ULL query(int l,int r){
    return h[r] - h[l-1]*p[r-l+1];
}
int main(){
    int n,m;
    cin>>n>>m;
    string x;
    cin>>x;

    //字符串从1开始编号，h[1]为前一个字符的哈希值
    p[0] = 1;
    h[0] = 0;
    for(int i=0;i<n;i++){
        p[i+1] = p[i]*P;            
        h[i+1] = h[i]*P +x[i];      //前缀和求整个字符串的哈希值
    }

    while(m--){
        int l1,r1,l2,r2;
        cin>>l1>>r1>>l2>>r2;
        if(query(l1,r1) == query(l2,r2)) printf("Yes\n");
        else printf("No\n");

    }
    return 0;
}

把字符串变成一个p进制数字（哈希值），实现不同的字符串映射到不同的数字
冲突问题：通过巧妙设置P (131 或 13331) 的值，一般可以理解为不产生冲突。
前缀和公式 h[i+1]=h[i]×P+s[i]
区间和公式 h[l,r]=h[r]−h[l−1]×P^r−l+1
区间和公式
ABCDE 与 ABC 的前三个字符值是一样，只差两位，
乘上 P的平方 把 ABC 变为 ABC00，再用 ABCDE - ABC00 得到 DE 的哈希值。

---

（三）搜索与图论

---

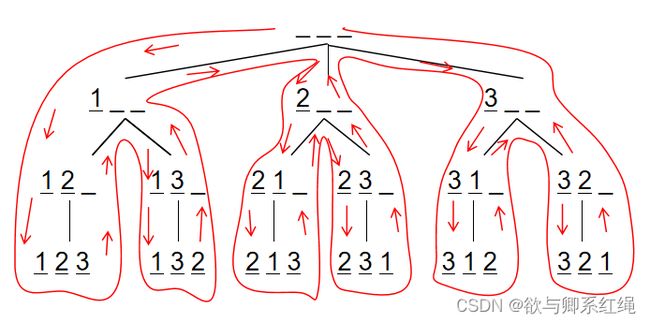
dfs

排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式
共一行，包含一个整数 n。

输出格式
按字典序输出所有排列方案，每个方案占一行。

数据范围
1≤n≤7
输入样例：
3
输出样例：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

#include 
using namespace std;
const int N = 10;
int n;
int path[N]; //保存数列的数组，不停进行覆盖的过程，只用到到n的几个位置
bool state[N]; //状态保存数组，1表示用过，0表示未用
void dfs(int u) //u表示现在处于树的第几层
{
    if(u==n)  //说明n个位置都已经排满，可以输出
{
    for(int i=0;i<n;i++) cout << path[i]<<" ";
    cout<<endl;
    return; //（不加也行）是为了返回上一层
}
for(int i=1;i<=n;i++) //代表n个位置上可以填的数
{
    if(!state[i])   //如果没被用过
    {
        path[u]=i;   //填到当前位置上
        state[i]=1;
        dfs(u+1);   //开始填下一个数
        state[i]=0;  //恢复现场，每次return的时候把状态归位
    }
}
}
int main()
{
    cin >> n;
    dfs(0);
}

dfs的一般结构：
void dfs(int step)
{
判断边界
尝试每种可能（for(i-1;i<=n;i++）
{
继续下一步(dfs(step+1))
恢复现场
}
}

---

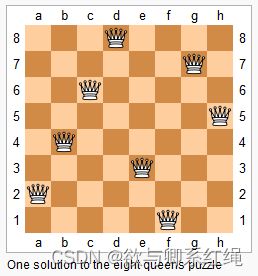
n皇后（dfs+剪枝）

n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式
共一行，包含整数 n。

输出格式
每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围
1≤n≤9
输入样例：
4
输出样例：
.Q…
…Q
Q…
…Q.

…Q.
Q…
…Q
.Q…

#include 
#include 
#include 
using namespace std;
const int N = 10;
char g[N][N];  //可以看做整个棋盘格
int n; //n*n棋盘
int col[N],dg[N],udg[N]; //代表列，对角线，反对角线（不用管行，行肯定不重复）
void dfs(int u)
{
    if(u==n) {   //所有行都遍历完了，完整棋盘形成了
        for (int i = 0; i < n; i ++ ) 
       cout<<g[i]<<endl;
      cout<<endl;
       return;
    }
    for(int i=0;i<n;i++) //遍历一行里的每一列
    {
        if(col[i]==0&&dg[i-u+n]==0&&udg[i+u]==0) //都没被放过皇后
        {
            g[u][i]='Q'; //皇后放这个格子
            col[i]=dg[i-u+n]=udg[i+u]=1;
            dfs(u+1);
            g[u][i]='.';  //恢复现场
            col[i]=dg[i-u+n]=udg[i+u]=0;
        }
    }
    
}
int main()
{
    cin >> n;
    for(int i=0;i<n;i++)
    for (int j = 0; j < n; j ++ ) g[i][j]='.';
    dfs(0);
    return 0;
}

解释一下两个对角线的下标，其实就是为了形成一个一一映射的关系，找出一个唯一的成对u，i对应的值。 这里找的是截距。

---

bfs

广搜的思想是一层层找出距离起点相同的点，每次距离长度加一

---

走迷宫

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。

数据保证 (1,1) 处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

输入格式
第一行包含两个整数 n 和 m。

接下来 n 行，每行包含 m 个整数（0 或 1），表示完整的二维数组迷宫。

输出格式
输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围
1≤n,m≤100
输入样例：
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例：
8

#include 
#include 
#include 
using namespace std;
typedef pair<int, int> PII;
int n,m;  //行，列
queue <PII> q;
const int N = 110;
int g[N][N],dis[N][N]; //存地图和距离
int bfs()
{
    memset(dis,-1,sizeof dis); //把距离归-1，后续可以判断出此点是否被搜索过
    dis[0][0]=0;
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1}; //表示一个点上下左右四点
    q.push({0,0}); //把起点入队 
    while(!q.empty())
    {
        PII t=q.front(); //以该点t为起始点，找周围距离为1的四点
        q.pop();
        for(int i=0;i<4;i++)
        {
            int x=t.first+dx[i]; 
            int y=t.second+dy[i]; //代表的是一个新找出来的点
            if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]==0&&dis[x][y]==-1)  //看这个点在不在边界里，能不能走，是不是第一次找出来
            {
                dis[x][y]=dis[t.first][t.second]+1;  //这个符合条件的点是上一个点距离加一
                q.push({x,y});
            }
        }
    }
return dis[n-1][m-1]; 
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i ++ )
     for (int j = 0; j < m; j ++ )
     scanf("%d",&g[i][j]);
     cout<<bfs()<<endl;
     
}

开数组存入能走的点的距离，最后终点坐标的数组存的就是起点到终点的最小值

---

八数码

在一个 3×3 的网格中，1∼8 这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。

例如：

1 2 3
x 4 6
7 5 8
在游戏过程中，可以把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1 2 3
4 5 6
7 8 x
例如，示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1 2 3 1 2 3 1 2 3 1 2 3
x 4 6 4 x 6 4 5 6 4 5 6
7 5 8 7 5 8 7 x 8 7 8 x
现在，给你一个初始网格，请你求出得到正确排列至少需要进行多少次交换。

输入格式
输入占一行，将 3×3 的初始网格描绘出来。

例如，如果初始网格如下所示：

1 2 3
x 4 6
7 5 8
则输入为：1 2 3 x 4 6 7 5 8

输出格式
输出占一行，包含一个整数，表示最少交换次数。

如果不存在解决方案，则输出 −1。

输入样例：
2 3 4 1 5 x 7 6 8
输出样例
19

#include 
#include 
#include 
#include 
#include 
using namespace std;
queue<string> q; //存字符串状态
unordered_map<string,int> dis;  //每种状态对应的步数
int bfs(string start)
{
    string end="12345678x";  //定义结束态
    q.push(start);
    dis[start]=0;
    int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
    while(!q.empty())
    {
        auto t=q.front();
        q.pop();
        int tdis=dis[t];  //先存上当前状态对应的步数，方便增加交换后的步数
        if(t==end) return tdis;  //已经交换完毕，返回步数
        int val=t.find('x');
        int x=val/3,y=val%3;  //字符串下标与矩阵下标的转换，记住
        for(int i=0;i<4;i++)
        { //分别枚举x上下左右的坐标，与x进行交换
            int xx=x+dx[i],yy=y+dy[i]; 
            if(xx>=0&&xx<3&&yy>=0&&yy<3)  //坐标没有出界
            {
                swap(t[val],t[xx*3+yy]);  
              if(!dis.count(t))  //这种状态还没被存
              {
                  dis[t]=tdis+1; //步数加一
                  q.push(t);  //新状态存上
              }
              swap(t[val],t[xx*3+yy]); //交换回来，为下次交换做准备
            }
            
        }
        
    }
    return -1;  //说明走不到，返回-1
}
int main()
{
    string start,c;
    for(int i=0;i<9;i++)
    {
        cin>>c;
        start+=c;
    }
    cout<<bfs(start);
    return 0;
    
}

队列存转换后的状态，hash表存每一状态对应的距离，就是变换了多少步
字符串下标与矩阵中下标的转换

数和图的广搜

---

图中点的层次

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环。

所有边的长度都是 1，点的编号为 1∼n。

请你求出 1 号点到 n 号点的最短距离，如果从 1 号点无法走到 n 号点，输出 −1。

输入格式
第一行包含两个整数 n 和 m。

接下来 m 行，每行包含两个整数 a 和 b，表示存在一条从 a 走到 b 的长度为 1 的边。

输出格式
输出一个整数，表示 1 号点到 n 号点的最短距离。

数据范围
1≤n,m≤10⁵
输入样例：
4 5
1 2
2 3
3 4
1 3
1 4
输出样例：
1

#include 
#include 
#include 
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],idx;
int n,m; //点数和边数'
int d[N]; //保存1号点和其余各点的距离
bool st[N];
void add(int a,int b)
{
    e[idx]=b;ne[idx]=h[a]; h[a]=idx++;   //邻接表构造模板（拉链法）
}
int bfs()
{
    memset(d,-1,sizeof(d));
    memset(st, 0, sizeof st);
    d[1]=0;
    queue<int> q;
    q.push(1);
    st[1]=1;
    while(!q.empty())
    {
        int t=q.front();
        q.pop();
        for(int x=h[t];x!=-1;x=ne[x])
        {
            int j=e[x]; //向外走一步
            if(!st[j])
            {
                d[j]=d[t]+1;  //距起点距离是上一步的点的距离加一
                q.push(j);  //把新扩张的点加入队列
                st[j]=1;
            }
        }
    }
    return d[n]; //即为点n与起点的距离
    
}
int main()
{
    memset(h,-1,sizeof(h));
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
    }
    cout<<bfs()<<endl;
}

广搜搜到的即为最短路

---

拓扑排序

给定一个 n 个点 m 条边的有向图，点的编号是 1 到 n，图中可能存在重边和自环。

请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。

若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。

输入格式
第一行包含两个整数 n 和 m。

接下来 m 行，每行包含两个整数 x 和 y，表示存在一条从点 x 到点 y 的有向边 (x,y)。

输出格式
共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。

否则输出 −1。

数据范围
1≤n,m≤10⁵
输入样例：
3 3
1 2
2 3
1 3
输出样例：
1 2 3

#include 
#include 
#include 
using namespace std;
int n,m; //点数和边数
const int N=1e5+10;
int e[N],ne[N],h[N],idx;
int d[N]; //点的入度
queue<int> q; 
void add(int a,int b)
{
    e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
void topsort() //拓扑排序
{
    int top[N]; //存放拓扑序列
    int cnt=1;
    for(int i=1;i<=n;i++)
    {
        if(!d[i])  //入度为零的点先入队
            q.push(i);
    }
    while(!q.empty())
    {
        int temp=q.front();
        top[cnt++]=q.front(); 
        q.pop();
        for(int nu=h[temp];nu!=-1;nu=ne[nu])
        {//删除temp发出的边
            int num=e[nu]; 
            d[num]--;
            if(d[num]==0) q.push(num); //如果入度为零，说明可以输出
        }
    }
    if(--cnt==n) //之前cnt多加一次，这里先减去
    for(int i=1;i<=n;i++) cout<<top[i]<<" ";
    else cout<<"-1";
}
int main()
{
    cin>>n>>m;
    memset(h,-1,sizeof(h));
    while (m -- )
    {
        int x,y;
        cin>>x>>y;
        d[y]++;
        add(x,y);
    }
    topsort();
    return 0;
}

首先记录各个点的入度

然后将入度为 0 的点放入队列

将队列里的点依次出队列，然后找出所有出队列这个点发出的边，删除边，同时边的另一侧的点的入度 -1。

如果所有点都进过队列，则可以拓扑排序，输出所有顶点。否则输出-1，代表不可以进行拓扑排序。

---

（四）数学知识

---

质数

---

试除法判断质数（暴力）

给定 n 个正整数 ai，判定每个数是否是质数。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式
共 n 行，其中第 i 行输出第 i 个正整数 ai 是否为质数，是则输出 Yes，否则输出 No。

数据范围
1≤n≤100,
1≤ai≤2³¹−1
输入样例：
2
2
6
输出样例：
Yes
No

#include 
using namespace std;
int n,x;
bool isprime(int n)
{
    if(n<2) return false;
    for(int i=2;i<=(n/i);i++)
    {
        if(n%i==0) return false;
    }
    return true;
}

int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&x);
        if(isprime(x)) cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

---

分解质因数

给定 n 个正整数 ai，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式
对于每个正整数 ai，按照从小到大的顺序输出其分解质因数后，每个质因数的底数和指数，每个底数和指数占一行。

每个正整数的质因数全部输出完毕后，输出一个空行。

数据范围
1≤n≤100,
2≤ai≤2×10⁹
输入样例：
2
6
8
输出样例：
2 1
3 1

2 3

#include 
using namespace std;
int main()
{
    int n;
    cin>>n;
    while (n-- )
    {
     int a;
     cin>>a;
     for(int i=2;i<=a/i;i++)
     {
        int s=0;  //存指数，即一个质因子的次方
         if(a%i==0)
         {
             while(a%i==0)
             {
                 s++;   //计算指数
                 a/=i;
             }
              cout<<i<<" "<<s<<endl;
         }
     }
     if(a>1)  //一个数判断的最后，如果a>1，一定是这个数本身，输出即可
     cout<<a<<" "<<1<<endl;
     cout<<endl;
    }
    return 0;
}

每个正整数都能够以唯一的方式表示成它的质因数的乘积。
最后如果n还是>1，说明这就是大于sqrt(n)的唯一质因子，输出即可

---

线性筛

给定一个正整数 n，请你求出 1∼n 中质数的个数。
1≤n≤10⁶

#include 
using namespace std;
const int N=1e6+10;
int primes[N]; //放质数
int cnt;
bool st[N]; //标志数组，1表示被筛出去，即不是质数
int get_prime(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!st[i])  primes[cnt++]=i;  //存入一个质数
        for(int j=0;primes[j]<=n/i;j++) //变形一下得到——primes[j]*i<=n，即筛小于等于n的合数
        {
            st[i*primes[j]]=true;  //用最小质因子筛掉合数
            if(i%primes[j]==0) break; //当发现primes[j]是i最小质因子的时候,如果再继续进行的话，
//我们就把 prime[j+1]*i 这个数筛掉了,虽然这个数也是合数，
//但是我们筛掉它的时候并不是用它的最小质因数筛掉的，而是利用 prime[j+1] 和 i 把它删掉的
//这个数的最小质因数其实是prime[j],如果我们不在这里退出循环的话，我们会发现有些数是被重复删除了的。
        }
    }
    return cnt;
}
int main()
{
    int n;
    cin>>n;
   int ans=get_prime(n);
   cout<<ans;
}

经典质数筛，记住

---

约数

试除法求约数

给定 n 个正整数 ai，对于每个整数 ai，请你按照从小到大的顺序输出它的所有约数。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式
输出共 n 行，其中第 i 行输出第 i 个整数 ai 的所有约数。

数据范围
1≤n≤100,
1≤ai≤2×10⁹
输入样例：
2
6
8
输出样例：
1 2 3 6
1 2 4 8

#include 
#include 
#include 
using namespace std;
int n;
void get(int x)
{
    vector<int> res;
    for(int i=1;i<=x/i;i++)
    {
        if(x%i==0) 
        {res.push_back(i);
        if(x/i!=i) res.push_back(x/i);
        }
    }
    sort(res.begin(),res.end());
    for(auto x:res)
    cout<<x<<" ";
    cout<<endl;
}
int main()
{
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        get(x);
    }
    return 0;
}

约数个数

给定 n 个正整数 ai，请你输出这些数的乘积的约数个数，答案对 10⁹+7 取模。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式
输出一个整数，表示所给正整数的乘积的约数个数，答案需对 109+7 取模。

数据范围
1≤n≤100,
1≤ai≤2×10⁹
输入样例：
3
2
6
8
输出样例：
12

#include 
#include 
using namespace std;
int n;
long long res=1;
const int N=1e9+7;
int main()
{
    cin>>n;
    unordered_map<int,int> hash;
    while (n -- ){
        int x;
        cin>>x;
        for(int i=2;i<=x/i;i++)
        {
            while(x%i==0)
            {
                hash[i]++;
                x/=i;
            }
        }
        if(x>1) hash[x]++;
    }
    for(auto i:hash) res=res*(i.second+1)%N;
    cout<<res;
}

N=p1^a1 p2^a2 p3^a3……
ans=(a1+1)(a2+1)(a3+1)……
即约数个数就是一个数的每个因子的指数加一相乘

---

约数之和

上面的条件，求约数的和
输入样例：
3
2
6
8
输出样例：
252

#include 
#include 
using namespace std;
typedef long long LL;
const int N=1e9+7;
int main()
{
    int n;
    cin>>n;
    unordered_map<int,int> hash;
    while (n -- )
    {
        int x;
        cin>>x;
        for(int i=2;i<=x/i;i++)
        {
            while(x%i==0)
            {
                hash[i]++;
                x/=i;
            }
        }
        if(x>1) hash[x]++;
    }
    LL res=1;
    for(auto i:hash)
    {LL a=i.first,b=i.second;
    LL t=1;
    while(b--) t=(t*a+1)%N; //加一因为有个零次方
    res=res*t%N; //答案就是把每次算的乘起来
    }
    cout<<res<<endl;
}

也是先存下每个因子的指数，
约数之和： (p1⁰+p1¹+…+p1^c1)∗…∗(pk⁰+pk¹+…+pk^ck)
c指的是因子对应的指数

---

求最大公因数（辗转相除）

输入示例：
2
3 6
4 6
输出样例：
3
2

#include 
using namespace std;
int gcd(int x,int y)
{
    //if(x%y==0) return y;
    //return gcd(y,x%y);
    return b?gcd(b,a%b):a;
}
int main()
{
    int n;
    cin>>n;
    while (n -- ){
        int a,b;
        cin>>a>>b;
        cout<<gcd(a,b)<<endl;
    }
    return 0;
}

（六）贪心

---

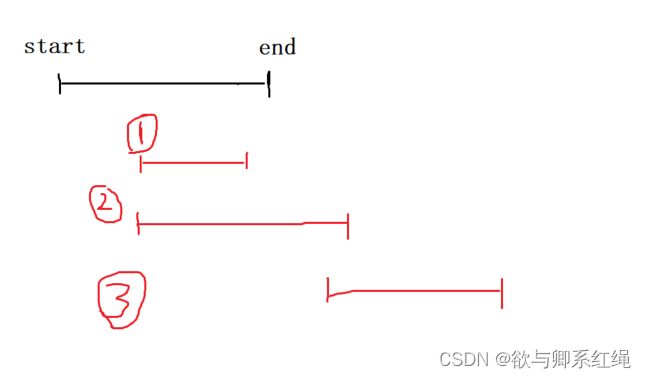
区间问题

---

区间选点/最大不相交区间数量

给定 N 个闭区间 [ai,bi]，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。

输入格式
第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式
输出一个整数，表示所需的点的最小数量。

数据范围
1≤N≤10⁵,
−10⁹≤ai≤bi≤10⁹
输入样例：
3
-1 1
2 4
3 5
输出样例：
2

#include 
#include 
using namespace std;
const int N=1e5+10;
int n; //区间数
struct range
{
    int l,r;
    bool operator<(const range &w)const
    {
        return r<w.r;    //重载小于号
    }
}range[N];   //定义出存区间的结构体
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int l0,r0;
        cin>>l0>>r0;
        range[i].l=l0,range[i].r=r0;
    }
    sort(range,range+n);  //基于右端点排序
    int res=0;int idx=-2e9; //idx存前一个区间的右端点
    for(int i=0;i<n;i++)
    {
        if(range[i].l>idx) //如果此区间的左端点严格大于上一区间的右端点
        {
            res++;
            idx=range[i].r;
        }
    }
    cout<<res;
    return 0;
}

经典贪心问题，先根据右端点进行排序，再根据下一区间左端点和上一区间的右端点的大小关系判断下一区间是否符合条件。
最终目的使答案区间两两不相交。

---

区间覆盖

给定 N 个闭区间 [ai,bi] 以及一个线段区间 [s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。

输出最少区间数，如果无法完全覆盖则输出 −1。

输入格式
第一行包含两个整数 s 和 t，表示给定线段区间的两个端点。

第二行包含整数 N，表示给定区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式
输出一个整数，表示所需最少区间数。

如果无解，则输出 −1。

数据范围
1≤N≤10⁵,
−10⁹≤ai≤bi≤10⁹,
−10⁹≤s≤t≤10⁹
输入样例：
1 5
3
-1 3
2 4
3 5
输出样例：
2

#include 
#include 
using namespace std;
const int N=1e5+10;
struct range
{
    int l,r;
    bool operator<(const range &w)const  //重载小于号
    {
        return l<w.l;
    }
}range[N];
int main()
{
    int st,ed,n;
    cin>>st>>ed>>n;
   for(int i=0;i<n;i++)
    {
        int x,y;
        cin>>x>>y;
        range[i].l=x;
        range[i].r=y;
    }
    int res=0;bool flag=0;  //判断有没有成功覆盖
    sort(range,range+n); //按左端点排序
    for(int i=0;i<n;i++)
    {
        int j=i,r=-2e9;
        while(j<n&&range[j].l<=st)
        {
            r=max(r,range[j].r);  //遍历区间，存下最大的右端点
            j++;
        }
        if(r<st)  {res=-1;break;} //不取等号，特殊情况ed=st，如果右端点不能覆盖起点
        res++; //说明这个区间可以用
        if(r>=ed) {flag=1;break;} //这一个区间就够使了
        st=r; //更新起点
        i=j-1; //下次从下一区间开始判断
    }
    if(flag) cout<<res;
    else cout<<"-1";
    return 0;
}

先将所有区间按左端点排序，从前向后枚举每个区间，在所有能覆盖st的区间中，选择右端点最大的区间，然后将st更新为最大的右端点。

---

区间分组

给定 N 个闭区间 [ai,bi]，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得组数尽可能小。

输出最小组数。

输入格式
第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式
输出一个整数，表示最小组数。

数据范围
1≤N≤105,
−10⁹≤ai≤bi≤10⁹
输入样例：
3
-1 1
2 4
3 5
输出样例：
2

//堆中存放每一组的右端点，堆顶是右端点的最小值(小根堆)
//比较区间左端点和堆顶，小于就开新组，大于并入堆顶这一组
#include 
#include 
#include 
using namespace std;
const int N=1e5+10;
struct range
{
    int l,r;
    bool operator<(const range &w)const
    {
        return l<w.l;
    }
}range[N];
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int x,y;
        cin>>x>>y;
        range[i].l=x;
        range[i].r=y;
    }
    sort(range,range+n);
    priority_queue<int,vector<int>,greater<int>> heap; //优先队列
    for(int i=0;i<n;i++)
    {
        if(heap.empty()||range[i].l<=heap.top())
        {
            heap.push(range[i].r);
        }
        else 
        {
            heap.pop();
            heap.push(range[i].r);
        }
    }
    cout<<heap.size();
}

1.先将所有区间进行排序
2.从前向后遍历
判断能否放到某个现有的组中 L[i]>堆顶
如果不存在这样的组，就开新组
如果存在，就放进去并更新堆顶
最后堆的元素个数就是组数

---

哈夫曼树

合并果子

在一个果园里，达达已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。

达达决定把所有的果子合成一堆。

每一次合并，达达可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。

可以看出，所有的果子经过 n−1 次合并之后，就只剩下一堆了。

达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以达达在合并果子时要尽可能地节省体力。

假定每个果子重量都为 1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使达达耗费的体力最少，并输出这个最小的体力耗费值。

例如有 3 种果子，数目依次为 1，2，9。

可以先将 1、2 堆合并，新堆数目为 3，耗费体力为 3。

接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 12，耗费体力为 12。

所以达达总共耗费体力=3+12=15。

可以证明 15 为最小的体力耗费值。

输入格式
输入包括两行，第一行是一个整数 n，表示果子的种类数。

第二行包含 n 个整数，用空格分隔，第 i 个整数 ai 是第 i 种果子的数目。

输出格式
输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。

输入数据保证这个值小于 231。

数据范围
1≤n≤10000,
1≤ai≤20000
输入样例：
3
1 2 9
输出样例：
15

#include 
#include 
#include 
using namespace std;
int main()
{
  int n;
  priority_queue<int,vector<int>,greater<int>> heap;
  cin>>n;
  while (n -- ){
      int a;
      cin>>a;
      heap.push(a);
  }
  int res=0;
  while(heap.size()>1)
  {
      int a=heap.top();heap.pop();
      int b=heap.top();heap.pop();
      res+=a+b;
      heap.push(a+b);
  }
  cout<<res;
  return 0;
}

使用小根堆维护所有果子，每次弹出堆顶的两堆果子，并将其合并，合并之后将两堆重量之和再次插入小根堆中。

---

排队打水

有 n 个人排队到 1 个水龙头处打水，第 i 个人装满水桶所需的时间是 ti，请问如何安排他们的打水顺序才能使所有人的等待时间之和最小？

输入格式
第一行包含整数 n。

第二行包含 n 个整数，其中第 i 个整数表示第 i 个人装满水桶所花费的时间 ti。

输出格式
输出一个整数，表示最小的等待时间之和。

数据范围
1≤n≤10⁵,
1≤ti≤10⁴
输入样例：
7
3 6 1 4 2 5 7
输出样例：
56

#include 
#include 
using namespace std;
const int N=1e5+10;
typedef long long LL;
int n;
int a[N];
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    cin>>a[i];
    LL res=0;
    sort(a,a+n);
    for(int i=0;i<n;i++)
    {
        res+=a[i]*(n-i-1); //公式
    }
    
  cout<<res;
 return 0;
}

推出公式，等待时间=啥，然后猜出来打水时间短的放前面，等待时间最短

---

货仓选址

在一条数轴上有 N 家商店，它们的坐标分别为 A1∼AN。

现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。

为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

输入格式
第一行输入整数 N。

第二行 N 个整数 A1∼AN。

输出格式
输出一个整数，表示距离之和的最小值。

数据范围
1≤N≤100000,
0≤Ai≤40000
输入样例：
4
6 2 9 1
输出样例：
12

#include 
#include 
#include 
using namespace std;
const int N=1e5+10;
int a[N];
int n;
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
    sort(a,a+n);
    int res=0;
    for(int i=0;i<n;i++)
    {
        res+=abs(a[i]-a[n/2]);
    }
    cout<<res;
    return 0;
}

就是选这几个点里中间的点，从0开始计可以避免奇数偶数的判断，可以自己画画

---

耍杂技的牛

农民约翰的 N 头奶牛（编号为 1…N）计划逃跑并加入马戏团，为此它们决定练习表演杂技。

奶牛们不是非常有创意，只提出了一个杂技表演：

叠罗汉，表演时，奶牛们站在彼此的身上，形成一个高高的垂直堆叠。

奶牛们正在试图找到自己在这个堆叠中应该所处的位置顺序。

这 N 头奶牛中的每一头都有着自己的重量 Wi 以及自己的强壮程度 Si。

一头牛支撑不住的可能性取决于它头上所有牛的总重量（不包括它自己）减去它的身体强壮程度的值，现在称该数值为风险值，风险值越大，这只牛撑不住的可能性越高。

您的任务是确定奶牛的排序，使得所有奶牛的风险值中的最大值尽可能的小。

输入格式
第一行输入整数 N，表示奶牛数量。

接下来 N 行，每行输入两个整数，表示牛的重量和强壮程度，第 i 行表示第 i 头牛的重量 Wi 以及它的强壮程度 Si。

输出格式
输出一个整数，表示最大风险值的最小可能值。

数据范围
1≤N≤50000,
1≤Wi≤10,000,
1≤Si≤1,000,000,000
输入样例：
3
10 3
2 5
3 3
输出样例：
2

#include 
#include 
using namespace std;
int n;
const int N=1e5+10;
struct mou
{
    int w,s;
    bool operator<(const mou&x)const
    {
        return (w+s)<=(x.w+x.s);
    }
}mou[N];
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int x,y;
        cin>>x>>y;
        mou[i].w=x;   mou[i].s=y;
    }
    sort(mou,mou+n);
    long long sum=mou[0].w;
    long long ans=0-mou[0].s; //考虑只有一只牛的情况，危险系数不加上自己的体重
    for(int i=1;i<n;i++)
    {
        ans=max(ans,sum-mou[i].s);  //最后找的是危险系数最大的
        sum+=mou[i].w;
    }
    cout<<ans;
    return 0;
}

按w+s的值从小到大，小的在上面，大的在下面垫着