深度学习 -- 神经网络
1、神经网络的历史
2、 M-P模型
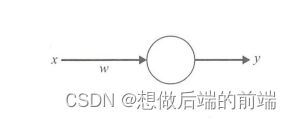
M-P模型是首个通过模仿神经元而形成的模型。在M-P模型中,多个输入节点![]() 对应一个输出节点y。每个输入x,乘以相应的连接权重w,然后相加得到输出y。结果之和如果大于阈值h,则输出1,否则输出0。输入和输出均是0或1。
对应一个输出节点y。每个输入x,乘以相应的连接权重w,然后相加得到输出y。结果之和如果大于阈值h,则输出1,否则输出0。输入和输出均是0或1。
公式2.1: ![]()
M-P模型可以表示AND和OR等逻辑运算。M-P模型在表示各种逻辑运算时,可以转化为单输入单输出或双输入单输出的模型。
取反运算符(NOT运算符)可以使用的单输入单输出的M-P模型来表示。使用取反运算符时,如果输入0则输出1,输入1则输出0,把它们代人M-P模型的公式(2.1),可以得到![]() ,
,![]()
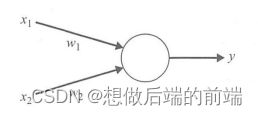
逻辑或(OR运算符)和逻辑与(AND运算符)可以使用双输入单输出M-P模型来表示。各运算符的输人与输出的关系如下表所示。根据表中关系,以OR运算为例时,公式(2.1)中的w,和h分别为w1=1,w2=1,h=0.5,把它们代人公式(2.1)可以得到下式:
公式2.2:![]()
以AND运算为例时,w1=1,w2=1,h=1.5,把它们代人公式(2.1)可以得到下式。
公式2.3:![]()
| 输入x1 | 输入x2 | OR运算符的输出 | AND运算符的输出 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
由此可见,使用M-P模型可以进行逻辑运算。但是,上述的w,和h是如何确定的呢?当时还没有通过对训练样本进行训练来确定参数的方法,只能人为事先计算后确定。此外,M-P模型已通过电阻得到了物理实现。
3、感知器
上节中的逻辑运算符比较简单,还可以人为事先确定参数,但且逻辑运算符w,和h的组合并不仅仅限于前面提到的这几种。罗森布拉特提出的感知器能够根据训练样本自动获取样本的组合。与M-P模型
需要人为确定参数不同,感知器能够通过训练自动确定参数。训练方式为有监督学习,即需要设定训练样本和期望输出,然后调整实际输出和期望输出之差的方式(误差修正学习)。误差修正学习可用公式(3.1)和(3.2)表示。
公式3.1:![]()
公式3.2:![]()
a是确定连接权重调整值的参数。a增大则误差修正速度增加,a减小则误差修正速度降低。
感知器中调整权重的基本思路如下所示。
- 实际输出y与期望输出r相等时,w和h不变
- 实际输出y与期望输出r不相等时,调整w,和h的值
参数w和h的调整包括下面这两种情况。
1:实际输出y=0、期望输出r=1时(未激活)
- 减小h
- 增大x7=1的连接权重w
- x=0的连接权重不变
2:实际输出y=1、期望输出r=0时(激活过度)
- 增大h
- 降低x=1的连接权重w
- x=0的连接权重不变
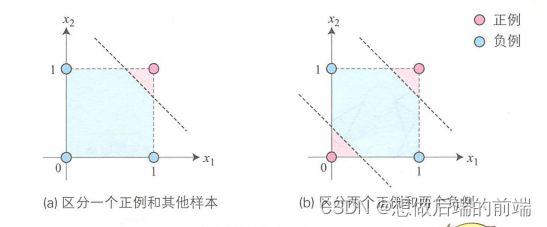
使用误差修正学习,我们可以自动获取参数,这是感知器引发的一场巨大变革。但是,感知器训练只能解决如下(a)图所示的线性可分问题,不能解决如下(b)图所示的线性不可分问题。为了解决线性不可分问题,我们需要使用多层感知器。
4、多层感知器
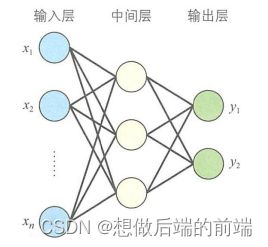
为了解决线性不可分等更复杂的问题,人们提出了多层感器印(multilayer perceptron)模型。多层感知器指的是由多多层结构的感知器递阶组成的输入值向前传播的网络,也被称为前馈网络或正向传播网络。
多层感知器通常采用三层结构,由输入层、中间层及输出层组成与公式(2.1)中的M-P模型相同,中间层的感知器通过权重与输入层的各单元(unit)相连接,通过阈值函数计算中间层各单元的输出值。中
间层与输出层之间同样是通过权重相连接。那么,如何确定各层之间的连接权重呢?单层感知器是通过误差修正学习确定输入层与输出层之间的连接权重的。同样地,多层感知器也可以通过误差修正学习确定两层之间的连接权重。误差修正学习是根据输入数据的期望输出和实际输出之间的误差来调整连接权重,但是不能跨层调整,所以无法进行多层训练。因此,初期的多层感知器使用随机数确定输入层与中间层之间的连接权重,只对中间层与输出层之间的连接权重进行误差修正学习。所以,就会出现输入数据虽然不同,但是中间层的输出值却相同,以至于无法准确分类的情况。那么,多层网络中应该如何训练连接权重呢?人们提出了误差反向传播算法。
5、误差反向传播算法
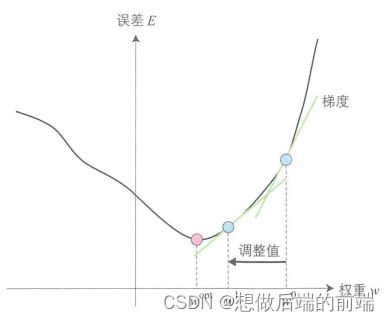
多层感知器中,输入数据从输入层输入,经过中间层,最终从输出层输出。因此,误差反向传播算法就是通过比较实际输出利期望输出得到误差信号,把误差信号从输出层逐层向前传播得到各层的的误差信号,再通过调整各层的连接权重以减小误差。权重的调整主要用梯度下降法(gradient descent method)。如图所示,通过实际输出和期望输出之间的误差E和梯度,确定连接权重w的调整值,得到新的连接权重w'。然后像这样不断地调整权重以使误差达到最小,从中学习得到最优的连接权重![]() 。这就是梯度下降法。
。这就是梯度下降法。
下面我们就来看看误差和权重调整值的计算方法。计算误差可以使用最小二乘误差函数(公式6.3)。通过期望输出r和网络的实际输出y计算最小二乘误差函数E。E趋近于0,表示实际输出与期望里输出更加接近。所以,多层感知器的训练过程就是不断调整连接权重w,以使最小二乘误差函数趋近于0。
接着再来看一下权重调整值。根据上述说明,权重需要进行调整以使最小二乘误差函数趋近于0。对误差函数求导就能得到上图中给定点的梯度,即可在误差大时增大调整值,误差小时减小调整值,所以连接权重调整值![]() 可以用公式(5.1)表示。
可以用公式(5.1)表示。
公式5.1:![]()
![]() 表示学习率,这个值用于根据误差的程度进行权重调整。
表示学习率,这个值用于根据误差的程度进行权重调整。
通过误差反向传播算法调整多层感知器的连接权重时,一个瓶颈问题就是激活函数。M-P模型中使用step函数作为激活函数,只能输出0或1,不连续所以不可导。为了使误差能够传播,鲁梅尔哈特等人提出使用可导函数sigmoid作为激活函数f(u)。
为了让大家更好地理解误差反向传播算法的过程,下面我们首先以单层感知器为例进行说明。根据复合函数求导法则,误差函数求导如下所示。
公式5.2:![]()
设y=f(u),求误差函数E对w的导数。
公式5.3:![]()
f(u)的导数就是对复合函数求导。
公式5.4:![]()
u对w,求导的结果只和x,相关,如下所示。
公式5.5:![]()
将公式(5.5)带入到公式(5.4)中得到下式。
公式5.6:![]()
这里对sigmoid函数求导。
公式5.7:![]()
下面就和单层感知器一样,对误差函数求导。
公式5.8:![]()
权重调整值如下所示
公式5.9:![]()
由上可知,多层感知器中,只需使用与连接权重![]() 相关的输入
相关的输入![]() 和输出
和输出![]() 即可计算连接权重调整值。
即可计算连接权重调整值。
下面再来看一下包含中间层的多层感知器。首先是只有一个输出单元y的多层感知器,如图所示。![]() 表示输入层与中间层之间的连接权重,
表示输入层与中间层之间的连接权重,![]() 表示中间层与输出层之间的连接权重。i表示输入层单元, j表示中间层单元。
表示中间层与输出层之间的连接权重。i表示输入层单元, j表示中间层单元。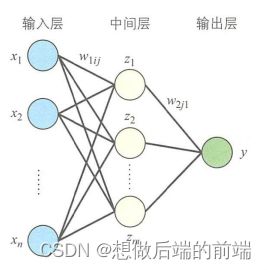
首先来调整中间层与输出层之间的连接权重。和上面的步骤聚一样,把误差函数E对连接权重![]() 求导展开成复合函数求导。
求导展开成复合函数求导。
公式5.10:![]()
与单层感知器一样,对误差函数求导。
公式5.11:![]()
这里的z表示的是中间层的值。于是,连接权重调整值如下所示。
公式5.12:![]()
接下来调整输入层与中间层之间的连接权重。输入层与中间层之间的连接权重调整值是根据输出层的误差函数确定的,求导公式如下所示。
公式5.13:![]()
与中间层与输出层之间的权重调整值的计算方法相同,输出y也是把公式展开后进行复合函数求导。与前面不同的是,这里是中间层与输出层单元之间的激活值![]() 对输入层与中间层之间的连接权重
对输入层与中间层之间的连接权重![]() 求导。
求导。![]() 由中间层的值
由中间层的值![]() 和连接权重
和连接权重![]() 计算得到。对
计算得到。对![]() 求导可以得到下式。
求导可以得到下式。
公式5.14:![]()
最后展开得到的输入层与中间层之间的连接权重调整值如下所示。
公式5.15:![]()
上述步骤的汇总结果如下图所示。由此可见,权重调整值的计算就是对误差函数、激活函数以及连接权重分别进行求导的过程。把得到的导数合并起来就得到了中间层与输出层之间的连接权重。而输入层与中间层之间的连接权重继承了上述误差函数和激活函数的导导数。所以,对连接权重求导就是对上一层的连接权重、中间层与输入层的激活函数以及连接权重进行求导的过程。像这种从后往前逐层求导的过程就称为链式法则(chain rule)。
同理下面让我们看一下有多个输出的多层感知器的权重调整:

多个输出与单个输出的不同之处在于,输入层与中间层之间的权重调整值是相关单元在中间层与输出层之间的权重调整总和。这就会出现无法调整链接权重。这就是误差反向传播算法中梯度消失导致无法调整链接权重。对于这个问题,需要在训练过程中调整学习率![]() 以防止梯度消失。
以防止梯度消失。
6、误差函数和激活函数
那么,有哪些函数可以作为误差函数呢?在多分类问题中,一般使用交叉恼代价雨数,公式如下所示 :
公式6.1:![]()
二分类中的函数则如下所示 :
公式6.2:![]()
递归问题巾使用最小二乘误差函数
公式6.3:![]()
这些是经常使用的误差函数,但误差函数的种类并不仅限于此,我们也可以根据实际问题自行定义误差函数 。
激活函数类似于人类神经元,对输入信号进行线性或非线性变换。 M-P模型中使用 step 函数作为激活函数,多层感知器中使用的 是 sigmoid 函数。 这里,用输入层与中间层之间,或中间层与输 出层之间的连接权重 ![]() 乘以相应单元的输入值
乘以相应单元的输入值 ![]() 并将该乘积之和经 sigmoid 函数计算后得到激活值 u。
并将该乘积之和经 sigmoid 函数计算后得到激活值 u。
公式6.4:![]()
公式6.5: ![]()
如下图蓝线所示,使用 sigmoid 函数时,如果对输入数据进行 加权求和得到的结果 u 较大则输 1,较小则输出 0。 而 M-P 模型中使 用的是 step 两数(如图中的红线所示),当 u 等于 0 时,输出结果 在 0和1 之间发生刷烈变动 。 另外, sigmoid 函数的曲线变化则较平缓 。
7、似然函数
我们可以根据问题的种类选择似然函数,计算多层感知器的输出结果。 多分类问题中,通常以 softmax函数(公式(7.1))作为似然函数
softmax函数的分母是对输出层所有单元(q=l, ...,Q) 的激活 值进行求和,起到了归一化的作用, 输出层中每个单元取值都是介于 0 和 l 之间的概率值,我们选择其中概率值最大的类别作为最终分类结果输出