模型性能评估（第三周）

一、模型评估

把数据集划分成训练集和测试集，用训练集训练模型和参数，然后在测试集上测试他的表现。如下图所示，第一行是线性回归通常的代价函数形式，我们需要将其最小化来获取参数、b。训练好模型，获得参数后，接下来使用第二第三行公式来分别计算测试集误差、训练集误差。

如果很小，很大，说明模型泛化能力弱。下图是二分类问题的公式：

对于分类问题，有一种更好的方法来评估。不是使用逻辑损失来计算测试误差，而是使用训练误差来衡量测试集的分数和算法错误分类的训练集的分数。例如，在二分类问题中，我们的预测值只有两种0\1，可以计算预测错误的个数count，可以表示成count/sum。

1.1 交叉验证测试集

上图中，我们打算拟合训练数据集，可以拟合成一次曲线、二次曲线等等。拟合出来参数后，可以使用测试数据集对其进行评估。假设我们已经计算出1-10次曲线的测试误差，经过对比，我们得到拟合5次曲线效果最好，那么我们就采取五次曲线的模型。

但是这种方法存在问题，因为可能会乐观估计泛化误差，也就是说估计值很有可能小于实际泛化误差。这是因为在我们在基本拟合过程中，有一个额外的参数d，即多项式的次数，我们使用测试集选择这个参数。也就是说，我们使用训练数据集选择、b参数，使用测试数据集选择d参数，测试数据集评判训练数据集训练的参数好坏，而没有一个标准来评判测试数据集训练参数的好坏。

那么如何解决这个问题呢？将数据集分成三个子集，即训练集、交叉验证集、测试集。可以使用下图中三个公式来计算训练误差、交叉验证误差、测试误差：

对于上一个问题，我们使用交叉验证集来检验拟合的好坏，选择交叉验证误差最低的模型。

 最后使用测试机，来计算该模型在新数据上表现的泛化误差估计值。

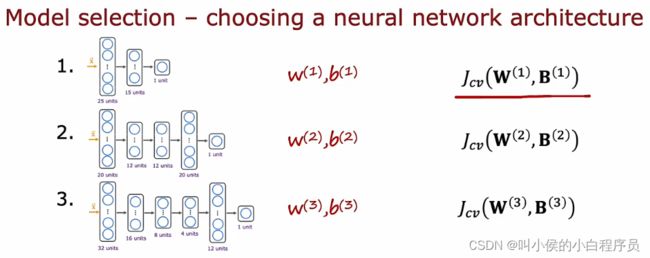
这种思路可以使用到其他地方，比如神经网络。如果你正在拟合一个手写数字识别模型，你可能会考虑下图中三个这样的模型。为了帮助您确定神经网络有多少层以及每层应该有多少个隐藏单元，您可以训练所有这三个模型并最终得到第一个模型的参数w1、 b1, 第二个模型的w2、b2、第三个模型的w3,b3。然后您可以使用交叉验证集评估神经网络性能，由于这是一个分类问题，最常见的是计算错误率（count/sum）。然后选择交叉验证误差最低的模型，使用此模型上训练的参数。最后如果您想计算泛化错误的估计值，则使用测试集来评估您刚刚选择的神经网络的性能。

只有在你决定选择这个模型作为你的最终模型之后，才可以在测试集上对其进行评估，并且因为你没有使用测试集做出任何决定，这可以确保你的测试集是公平的而不是过度的对您的模型对新数据的泛化能力的乐观估计。

1.2 偏差

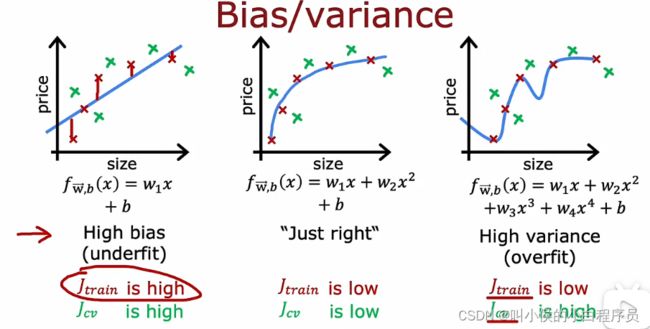
如下图所示，左边图高偏差（欠拟合），右边图高方差（过拟合） ，中间图拟合的刚刚好。下图中只有一个变量x，可以将拟合结果可视化，直观地看拟合的好坏。但是变量多的情况下，需要一种更系统的诊断方法找出您的算法是否具有高偏差或高方差，以此来查看您的算法在训练集和交叉验证集上的性能。

左图高，高；右图很低，但是高。因此高，高可以看作高偏差的指标；很低，但是高可以看作高方差的指标。

 1.3 正则化

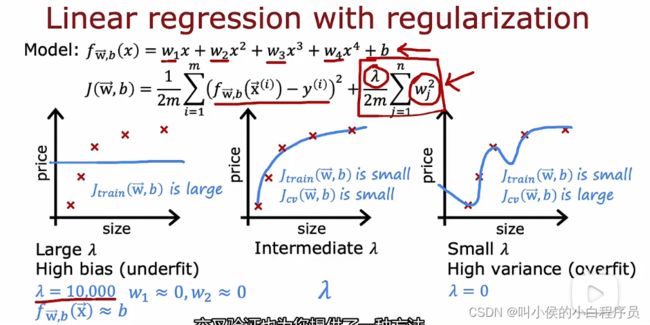
下图中，我们使用四阶多项式模型来拟合数据。左边正则化参数非常大，当最小化时，权重会非常小，基本趋近于0，因此f约等于b，拟合出来的曲线像一条直线，具有高偏差。右边非常小，当最小化时，会出现过拟合的现象。

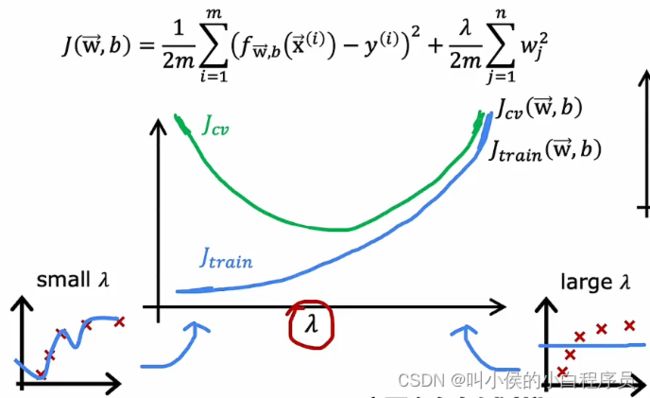
那么怎么来选择一个适度的呢？如下图所示，使用训练集进行训练，获得参数后，使用交叉验证集进行测试，计算交叉验证集的误差。选择不同的，计算对应地交叉验证集误差，选择最小的的那个。

下图是，随着的变化而变化的大概曲线图：

 1.3.1 性能评估的基准

例如一个语音识别系统，当我们仅仅计算了 =10.8%，=14.8%，我们没有一个基准来判断这个误差属于高还是低。此时可以这样解决问题：测试人类的表现错误水平，假设是10.6%，这样看的话，训练误差很小，但是交叉验证集误差有点大。还可以这样做：跟别人写的模型的表现水平做对比。

综上所示，训练误差  与基准水平的差值---表现了偏差大小；交叉训练集误差与训练集误差的差值----表现了方差的大小。

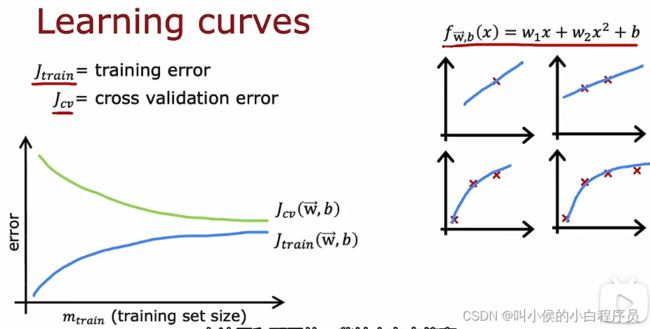
1.4 学习曲线

假设我们训练二次拟合曲线，绘制一张，随着训练集大小变化的曲线（学习曲线），如下图所示。随着训练集变大而变小，这是因为训练集越大，得到的模型参数就会越好，他的泛化能力越好。但是却随着训练集变大而变大，这是因为，当是一个数据的时候，很容易找到一个曲线适应这个数据，当时两个或者三个的时候，也很容易找到一个基本0误差的曲线去拟合，但是随着训练数据增大，就很难再找到这样的曲线了，如下图右边所示。

学习曲线还有一个特点，那就是 通常大于。

上图是在一个一次曲线上拟合的学习曲线，显然存在欠拟合（高偏差）的问题。即使训练集再多，他的，也会很大，远远高于基准水平。如果再加大训练数据，，曲线基本变得平坦，不会有太多的变化。这个现象给我们一个启发：通常高偏差问题，我们需要加大训练数据集来解决，但是如果不论怎么加大训练数据集，仍然存在高偏差，就需要考虑换个模型了。

上图是在一个四次曲线上拟合的学习曲线，存在过度拟合（高方差）的问题，最开始Jcv远大于Jtrain，且Jtrain远小于基准水平。在这种情况下仅仅通过增加训练集的大小来降低交叉验证误差并让你的算法表现得越来越好，这与高偏差情况不同，在这种情况下你唯一要做的就是 获得更多的训练数据，但是实际上并不能帮助您了解算法性能。

二、优化模型

2.1 误差分析

假如我们正在做一个识别垃圾邮件的模型，当模型测试的时候，发现500个交叉测试集中有100个被错误分类的邮件。我们分析被错误分类的邮件的特征：1、是关于制药的邮件。2、单词拼写错误的邮件。3、试图窃取密码的邮件。4、网络钓鱼电子邮件。5、文字内容写在图片上的邮件。然后把这100个错误分类的邮件按照前面五个类别进行分类计数。假设第一类有21封，2--3，3--7，4--18，5--5。我们由此可以知道制药的邮件、试图窃取密码的邮件、网络钓鱼电子邮件这三类被错分的概率很大，我们需要优先解决。

当我们的交叉测试集有5000个，错误分类的有1000个，这个数字量不允许人工分类，此时可以在1000封当中任意选取100个进行误差分析。

分析出错误的大概率来源了，那么我们该如何解决呢？1、增加关于制药的垃圾邮件的训练数据，让模型更好的学习如何识别垃圾邮件。2、查看邮件当中是否有URL，以此来判断是否为网络钓鱼电子邮件。

2.2 数据增强和数据合成

用现有训练数据创造新的训练数据。

例如数字字母识别，可以把图片放大缩小，旋转、镜像，畸变都可以创建新的数据，但是没有改变他是字母A的事实。

例如音频识别，可以把某个纯净的说话音频和某些噪声音频相结合，以此来创造出新的音频。但是在音频上加上畸变（例如某些文字咬字不清晰），这样的新数据不太好，因为现实当中不太可能出现。

因此做数据增强时，不能一味地增加新数据，要看数据是否对训练模型有好处，是否符合现实。

2.3 迁移学习

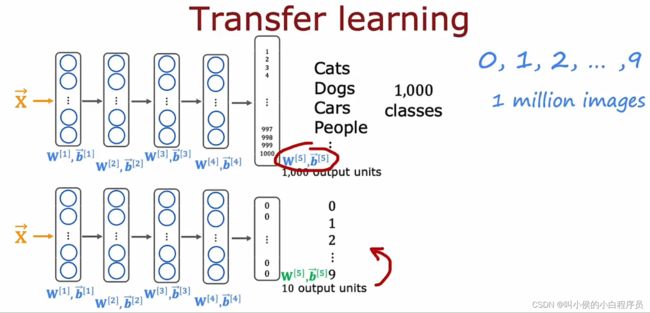
假如你想训练数字识别，但是有关于数字的图片不是很多。然而你有1百万张，1000个分类的动物图像，你可以构建一个网络模型训练识别1000个动物，如下图中上边的网络模型。这个模型有4层隐藏层，一个输出层，每一层的参数都标注出来了。

要是想利用迁移学习，可以这样操作：将上边的隐藏层模型以及参数直接拿过来用，但是输出层要重新设计。也就是说在迁移学习中，你可以做的是使用前四层的参数，实际上是除最终输出层之外的所有层作为参数的起点，然后运行优化算法，例如梯度下降或Adam优化算法使用来自该神经网络的值在顶部初始化的参数。

如何训练下边的神经网络有两种选择，1、将参数W1、B1， W2、B2到W4、B4作为顶部的值，并固定它们然后使用随机梯意下降或Odan等算法仅更新W5，B5，以降低您用于学习从小训练集中识别数字 0到9的通常成本函数。2、训练网络中的所有参数包括W1、B1， W2、B2直到W5，B5，但前四层参数的初始值将使用你在上面训练过的数值。

如果你有一个非常小的训练集，那么选项1可能会好点，但如果你有一个稍微大点的训练集，那么选项2可能会好一点。上边训练的网络已经让模型具备一些处理图像的基本能力，然后通过将这些数转移到新的神经网络。新的神经网络从一个更好的参数地方开始，这样我们就可以进一步学习一点点。这两个步路首先在大型数据集进行训练，然后在较小的数据集上进一 步调整参数，这一步被称为监督预训练。

第二步称为微调，您可以在其中获取己初始化或从 监督预训练中获得的参数，然后进一步运行梯度下降微调权重以适应您可能想有的手写数字识别的特定应用。

但是迁移学习也有弊端，那就是重新训练的网络需要和监督预训练网络的输入保持一致。例如同等大小尺寸的照片。

三、机器学习项目的完整周期

1、确定项目做什么

2、确定训练机器学习系统需要什么数据

3、训练模型，错误分析，迭代改进

4、在生产环境中部署

四、倾斜数据集的误差指标

假如训练一个判断是否患病的二分类模型，如果患病y=1，否则y=0。假如在测试集上的误差等于1%，这听起来是一个很不错的模型。

但是，假如这个疾病的患病率仅仅为0.5%，也就是意味着y大概率等于0。如果有三个模型，他们的误差（计算方法同前面的文章）分别为0.5%、1%，1.2%。第一个模型数据看起来非常好，他的误差是最小的，但是实际当中，他的表现可能不够好。这是因为，如果我让模型一直输出y=0，那么这个模型的错误率也仅仅0.5%。可能实际当中，反而第二个模型的表现最优。

这就引发一个思考：在处理偏斜数据集的问题时，我们通常使用不同的误差度量，而不仅仅是分类误差，来确定学习算法的性能。这个问题怎么解决呢？

如上图所示，我们可以计算精确度/召回率来解决这个问题。表格当中，上边的1/0表示实际患病/不患病（实际中正确的分类），左边的1/0表示预测患病/不患病（模型的分类结果）。假如交叉验证集中有100个数据，其中实际患病预测患病的人数有15（称为真阳性），实际患病预测不患病的人数有10（称为假阴性），实际不患病预测患病的人数有5（称为假阳性），实际不患病预测不患病的人数有70人（称为真阴性）。

精确度=真阳性/（真阳性+假阳性），召回率=真阳性/（真阳性+假阴性）。所以这个模型的精确度为0.75，召回率为0.6。这两个指标可以帮助检测模型是否一直输出y=0，这样的模型即使误差低，但是没有任何实际意义。如果一直y=0，那么precision=recall=0。

4.1 精确度和召回率的权衡

精确度意味着预测患病后有多大概率真正诊断为患病；召回率意味着 如果患者真正患有这个罕见疾病有多大概率被预测出来。这两个指标当然越大越好，但是通常情况下，这两个指标需要被权衡。

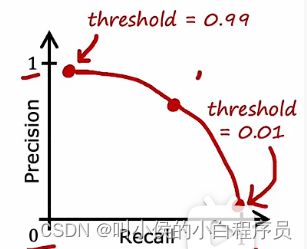
通常情况下，我们做逻辑回归算法时，将阈值设置为0.5，也就是说，当输出值大于等于0.5时就预测为1。如果将阈值设置为0.7，这意味着只有当我们有更大的把握时，才将患者预测为患病，这样的做法会提高精确度，但是降低了召回率。如果这种疾病不那么危险的时候可以这样做！

如果疾病是一个代价比较严重的疾病，我们期望召回率更高，此时可以降低阈值。下图是精确度和召回率随着阈值变换的曲线图：

有没有一种方法可以权衡精确度和召回率呢？1、取平均值，但是这种方法不太好。如下图中的数据，算法1P和R之间较为均衡，算法2P高，算法3R高，凭借直觉很难评价三种算法哪个更合适。如果取平均值的话，算法1是0.45，算法2是0.4，算法三是0.501（平均值主要受这些值中高的那一个影响），显然算法三更高，但是实际上，他的精确度太过于低了，不是很好的算法。因此求平均值不是一个好方法。

2、F1分数，是一种结合（P和R）精度和召回率的方法，但它更强调这些值中较低的那个。实际当中，如果算法的P或者R非常低，那么这个算法是没有意义的（求平均值更加关注大的值，会把小的值隐藏掉，从而造成对算法评论的不科学性）。F1分数的公式如下所示：