机器学习中的数据归一化、最值归一化、均值方差归一化（标准化）

为什么要进行数据归一化

我们来考虑这样一个场景，我要使用KNN算法来预测一个人的职业。目前我们提取到了一批数据，如下：

工作年限	工资	职业
1	8000	程序员
2	12000	程序员
3	15000	程序员
4	18000	程序员
1	3000	土木工程
2	3500	土木工程
3	4000	土木工程
4	4500	土木工程

我们根据数据得出以下图像：

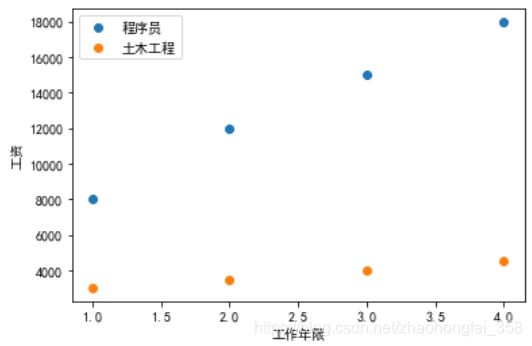
这个图像乍一看，好像没什么问题。但是当我们要预测时，就会发现问题很大。比如，我们来了一条数据 1年工作经验6000工资的，它与第二条数据计算欧拉距离时，公式为：

$$Distance=\sqrt{(12000-6000{)}^2+(2-1{)}^2}$$

这时我们发现纵坐标的数据要远大于横坐标。这样我们在计算距离时，由于工资的影响远大于工作年限，所以预测相当于只采用了一个特征。

由于这个原因，所以我们要进行数据归一化

什么是数据归一化

数据归一化就是将所有的数据映射到同一尺度，即让每一个特征数据的影响力是相同的

常用的两种归一化方式：

• 最值归一化
• 均值方差归一化

最值归一化（Normalization）

最值归一化（normalization），也称为归一化：把所有数据映射到0-1之间，如下图所示：

最小值映射成0，最大值映射成1。中间的值映射到对应位置。

公式为：

$$x_{scale}=\frac{x-x_{min}}{x_{max}-x_{min}}$$

其中 $x_{max}$ 和 $x_{min}$ 是指要归一化数据的最大边界和最小边界。$x$ 为归一化之前的数值，$x_{scale}$ 为归一化之后的数值。

为什么这个式子可行呢？可以通过例子来理解。还以上面的例子，假设我们只预测工作经验0-5，工资3000-20000的人。其他的数据一概不考虑。

我们归一化之后的数据为：

工作年限	工资	职业	工作年限（归一化后）	工资（归一化后）
1	8000	程序员	0.2	0.29411765
2	12000	程序员	0.4	0.52941176
3	15000	程序员	0.6	0.70588235
4	18000	程序员	0.8	0.88235294
1	3000	土木工程	0.2	0
2	3500	土木工程	0.4	0.02941176
3	4000	土木工程	0.6	0.05882353
4	4500	土木工程	0.8	0.08823529

工作年限 1年，1在0-5之间20%的这个位置，所以它归一化之后为0.2。其他同理

在归一化后，我们再对这个图进行绘制：

这次横纵坐标都是在0-1范围之间的，计算距离时，每个特征的影响力也都一样了

最值归一化的适用性

最值归一化只适用于有明显边间的情况，例如 学生的成绩（0-100分），像素点的像素值（0-255）

对于没有明显的边界，如工资（有人可能好几百万，甚至好几千万）。若大部分的收入都在10k左右，突然有一个人收入是1000w，这样如果强行使用最值归一化，那么数据点全都集中在了最左侧。这样显然是不够好的。此时，可以使用均值归一化

在上述例子中，我们再增加一条工资特别高的程序员：

工作年限	工资	职业
1	8000	程序员
2	12000	程序员
3	15000	程序员
4	18000	程序员
20	10,000,000	程序员
1	3000	土木工程
2	3500	土木工程
3	4000	土木工程
4	4500	土木工程

如果我们依然采取最值归一化，那么归一化后的结果为：

可以看到，蓝色的点和黄色点都已经重合了，且分布在最下层，而大佬在右上角。这样的归一化显然不合适。

均值方差归一化（Standardization）

如果你对方差、标准差、正态分布等没有概念，请参考这篇文章。

均值方差归一化，也称为标准化。英文也叫作Z-score Normalization，它是把所有数据归到均值为0，方差为1的分布中。即确保最终得到的数据均值为0，方差为1。

公式为：

$$x_{scale}=\frac{x-\mu }{S}$$

其中 $x$ 为要归一化的值，$x_{scale}$ 为归一化之后的值。$\mu$ 为样本的平均值，$S$ 为样本的标准差。

为什么要这么归一化呢？

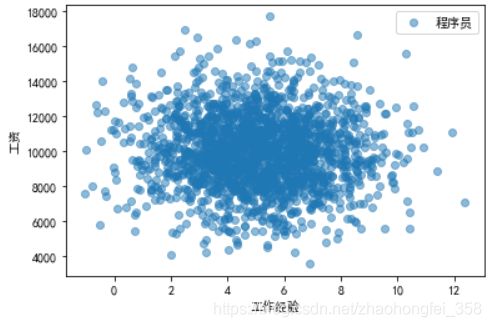
在自然界中，大部分的数据都是符合正态分布的。我们来生成一组符合正态分布的数据：

可以看出，该图的工作经验和工资都是符合正态分布的。其中：工资的平均值 $\mu =10,000$，标准差 $S=2000$；工作经验的平均值 $\mu =5$，标准差为 $S=2$

在当前情况下，他们的量纲不一样，所以需要对其进行处理：

1. 首先要做的第一步就是平移，即改变平均值 $\mu$。使工资和工作年限的平均值都为0。这样并不会改变各个点之间的距离。
   
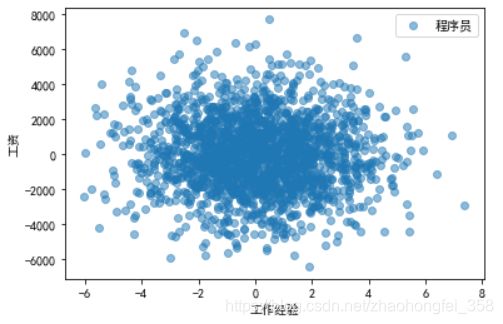
   可以看到，除了坐标平移之外，图的样子并没有发生改变

2. 第二步，我们要对每一个点的大小进行压缩。，标准差可以理解为平均每个点距离平均值的距离（不严谨）。先以工资为例，目前平均值为0，平均每个点距离0的距离为2000。如果我们把2000压缩成1，就完成了数据压缩。工作经验同理。这样的话，它们两个特征每个点距离0的量纲就保持一致了
   
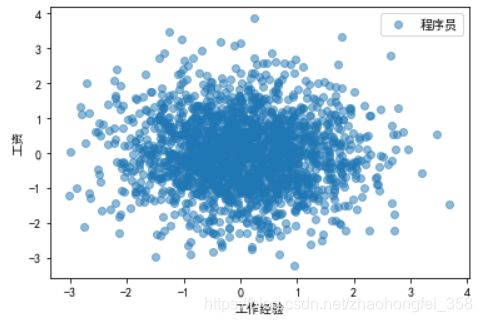
   此时，均值归一化（标准化）就完成了。工资和工作经验都为均值为0，方差为1的正态分布了。

均值方差归一化公式

将一个标准正态分布转化为一个普通正态分布，公式如下：

$$Y_i=\sigma \cdot X_i+\mu$$
其中，X为标准正态分布中的元素，$\mu$为平均值，$\sigma$ 为标准差。

所以，我生成正态分布工资数据时的代码如下：

salary = 2000 * np.random.randn(1000) + 10000 # 2000为标准差，10000为均值。1000为数据样本数

将上述公式反过来，即为普通正态分布转为标准正态分布

$$X_i=\frac{Y_i-\mu }{\sigma }$$

参考文献

---

Standardization in machine learning： https://www.linkedin.com/pulse/standardization-machine-learning-sachin-vinay/?trk=public_profile_article_view

4-7 数据归一化: https://coding.imooc.com/class/chapter/169.html