论文笔记：Threshold and Multi-signature Schemes from Linear Hash Functions

Tessaro, S., Zhu, C. EUROCRYPT 2023. Threshold and Multi-signature Schemes from Linear Hash Functions
https://link.springer.com/chapter/10.1007/978-3-031-30589-4_22
推广最有效的基于离散对数的方案MuSig2 (Nick, Ruffing, and Seurin, CRYPTO ’ 21)和FROST (Komlo and Goldberg, SAC ’ 20)，以使用适当定义的线性哈希函数。

前置阅读：https://blog.csdn.net/jiongxv/article/details/131390649整理了本文所使用的代数基础和引用知识。

摘要

本文给出了两轮多重签名和阈值签名的新结构，其安全性仅依赖于(普通)离散对数问题的硬度或RSA的硬度，以及假设随机预测。它们的签名协议是部分非交互式的，也就是说，签名协议的第一轮独立于被签名的消息。
我们通过推广最有效的基于离散对数的方案MuSig2 和FROST来获得我们的结构，以使用适当定义的线性哈希函数。虽然原始方案依赖于更强且更有争议的多离散对数（OMDL）假设，但我们证明了哈希函数的适当实例可以使安全性基于普通离散对数假设或RSA。我们的方案产生的签名与冈本的识别方案(CRYPTO ’ 92)中获得的签名等效。

Introduction

动机：特定的实现约束使得基于离散对数或RSA问题变体的无配对方案在一些上下文中具有吸引力。
目的：在最弱的假设条件下建立最佳的无配对多重签名和阈值签名。

方案是应用于两种最有效的基于dl的方案FROST和MuSig2的相同范例的结果。
方法的主要组成是线性哈希函数。观察到FROST和MuSig2都可以通过用线性哈希函数$\mathrm{F}:\mathcal{D}\to \mathcal{R}$替换幂映射$x\to g^x$来自然地推广，其中$\mathcal{D},\mathcal{R}$是field $\mathcal{S}$的$\mathcal{S}$模。通常将这些实例称为FROST-H和MuSig2-H。

特别要求: $F$是$\mathcal{S}-modules$的满同态，单不是单同态。

然后，定义了OMDL假设的自然模拟，我们将其称为Algebraic One-More Preimage Resistance(AOMPR)。
粗略地说，相应的安全博弈允许攻击者获得多个挑战$X_i=F(x_i)$其中$x_i\leftarrow \mathcal{D}$随机，攻击者还可以访问一个反转神谕(inversion oracle):输入$X\in \mathcal{R}$，返回$X$在$F$下的原像集合中的一个元素。(这使得假设是可证伪的，因为oracle可以有效地回答这样的反转查询。)为了赢得游戏，攻击者被要求在最多q次查询反转预言后反转q +1次挑战。
两个安全性结论：

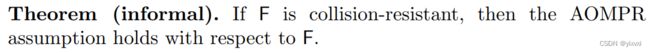
DL-Based Instantiations

实例化LHF

为了获得基于离散对数(DL)问题的FROST-H和MuSig2-H的实例化，可使用Pedersen线性哈希函数
当$g,Z$是大小为素数$p$的群的生成元时，在DL的困难性下具有抗碰撞性。

实例化签名

• 签名私钥$x\in {\mathbb{Z}}_p$公钥$\mathrm{pk}={\mathrm{g}}^{\mathrm{x}}$，签名形式（这是一种用Pedersen LHF代替离散对数映射的schnorr签名）：
  
  其中H是一个哈希函数，在我们的证明中被建模为随机的oracle。

• 验证签名$(R,a^{\prime },b^{\prime })$，查验$g^{a^{\prime }}{Z}^{b^{\prime }}=R\cdot p{k}^{H(pk,m,R)}$

对比一下原始schnorr签名： $(R=g^r,s=r+c\cdot sk)$，其中随机采样的$r$对应于$F$的输入$(a,b)$。schnorr验证签名：$g^s=R\cdot p{k}^c$。

对比一下okamoto方案： https://link.springer.com/content/pdf/10.1007/3-540-48071-4.pdf#page=40

• $sk=(s{k}_1,s{k}_2),pk=(p,q,g,Z,t,v)$，其中$v=g_1^{-s_1}{g}_2^{-s_2}$
• 签名方案：随机选取$(a,b),R=g^a{Z}^b,c=H(m,R)$
  签名$(c,y_1=a+c\cdot s{k}_1,y_2=b+c\cdot s{k}_2)$
• 验证：计算$R^{\prime }=g^{y_1}{Z}^{y_2}{v}^c$，验证$c^{\prime }=H(m,R^{\prime })=c$

这个方案与Okamoto方案的区别：后者使用了私钥$(x_1,x_2)\in {\mathbb{Z}}_p^2$，签名形式为：
这个方案相当于一个特例：$(x_1,x_2)=(x,0)$

总结：虽然MuSig2和FROST产生有效的Schnorr签名，但基于DLL的FROST- H和MuSig2- H实例产生的签名效率略低，并且有效地与Okamoto的签名兼容。
这种优化是通用的，可以直接应用于Okamoto的方案;但是，它对于阈值签名特别有利，因为它允许我们利用任何分布式密钥生成协议来进行Schnorr签名。

RSA-Based Instantiations

RSA的情况稍微复杂一些，因为上述框架似乎不直接支持RSA实例化:没有自然的基于RSA的线性哈希函数实现适当的$\mathcal{S}$模块。然而，我们证明了该框架可以适应支持基于rsa的线性哈希函数：基于公共参数$par=(N,e,w)$，其中$N$是RSA模，$e\in {\mathbb{Z}}_N^{\ast }$是一个素数满足
我们把这个线性哈希函数称为RLHF。在这里，重要的是要注意支持的标量空间被设置为$\mathcal{S}:=\mathbb{Z}$，这只是一个环。(我们把这样的哈希函数称为弱线性哈希函数。)

分析：这个$F$满足LHF的定义吗？弱体现在哪。

• 1：有$\mathcal{S}:=\mathbb{Z}$，$\mathcal{D}\in {\mathbb{Z}}_e\times {\mathbb{Z}}_N^{\ast },\mathcal{R}\in {\mathbb{Z}}_N^{\ast }$是$\mathcal{S}-module$，但是$\mathcal{S}$是ring而不是标准定义中的field。
• 2：确定性函数，这个映射是满同态，且不是单同态。

实例
密钥$sk=x\in {\mathbb{Z}}_N^{\ast },pk=x^e,m\in \{0,1{\}}^{\ast }$
签名$\sigma =(R=a^e{w}^b,s=a\cdot x^{H(pk,m,R)},b)$
验证$s^e{w}^b=R\cdot p{k}^{H(pk,m,R)}$

Schemes Based on Linear Hash Functions

对于素数大小为$p$的循环群$\mathbb{G}$和生成元$g$，我们可以把描述为$(\mathcal{S},\mathcal{D},\mathcal{R},F)$的线性哈希函数的描述看作类似于$(\mathbb{G},p,g)$的描述，其中$\mathcal{R}$对应于群$\mathbb{G}$，函数F下的原像对应于以$g$为底的离散对数，$\mathcal{S}$对应于标量${\mathbb{Z}}_p$的域。
此外，AOMPR游戏也类似于AOMDL游戏。这提供了一种将任何在AOMDL假设下安全的方案转换为由线性哈希函数构造并在AOMPR假设下安全的方案的一般方法。在本节中，我们将讨论如何将此思想应用于两个具体示例:MuSig2[43]，一个多签名方案，FROST[37]，一个阈值签名方案。

multi-signatures

MuSig2[43]是一个带密钥聚合的两轮多签名方案。此外，第一轮签名是消息独立的。我们首先给出了如下[43]的两轮多重签名的语法和安全性定义，然后提出了由MuSig2转化而来的基于LHF的新方案MuSig2- h，最后证明了新方案在AOMPR假设下的安全性。

语法

具有密钥聚合的两轮多重签名方案是一组高效(随机)算法$MS=(Setup,KeyGen,KeyAgg,PreSign,PreAgg,Sign,SignAgg,Ver)$行为如下。
(确定性)密钥聚合算法KeyAgg将大小不超过$2^{\kappa }$的多集公钥L作为输入，并返回聚合公钥$apk$。

$Ver(apk,m,\sigma )\to 0/1$

安全

多重签名的安全概念被称为MS-UF-CMA，它保证不可能伪造至少涉及一个诚实方的有效多重签名。

在游戏中，我们假设对手破坏了聚合器节点和除一个签名者外的所有签名者，并且可以与诚实方进行任意数量的(并发)签名会话。

MuSig2-H方案

它是由MuSig2转换而来，带有参数$v=4$，其中$\nu$表示在签名协议的第一轮中生成的随机数

对比一下原方案MuSig2：https://link.springer.com/chapter/10.1007/978-3-030-84242-0_8

可以看出将密钥生成替换/泛化成线性哈希函数$F$，参数取值由具体的${\mathbb{Z}}_p$一般化为$\mathcal{D}$，不同哈希函数的区分等。其他构造基本相同。
（所以说这个构造是LHF版本的MuSig2）
显然这个签名是两轮的，第一轮与签名的消息无关。

Threshold Signatures

FROST1和更有效的版本FROST2是(部分)非交互式阈值签名方案。

语法

$TS=(Setup,KeyGen,SPP,LPP,LR,PS,Agg,Vf)$，其行为如下。参与者是一个领导者和n个签名者。

• 算法$Setup(1^{\kappa })$初始化每个签名者的状态$s{t}_i\in [n]$和领导者的状态$s{t}_0$，并返回一个系统参数$par$。
• 密钥生成算法KeyGen()为每个签名者$i$返回一个公共验证密钥$pk$、公共辅助信息$aux$和一个秘密密钥$s{k}_i$。
• 
  其中
  
• 验证算法$Vf(pk,m，\sigma )$输出一个比特。

安全

阈值签名的安全概念TS-SUF-2和TS-SUF-3，它们分别是由FROST2和FROST1实现的。
TS-SUF-2和TS-SUF-3要求存在一种高效的强验证算法$SVf$，该算法将公钥$pk$、leader request $lr$和签名$\sigma$作为输入，并输出一个比特来表示$\sigma$是否合法地为$lr$获得。

TS-SUF-2保证攻击者只有在接收到来自至少$t-|CS|$个诚实方的相同领导请求$lr$的部分签名时才能生成$m$的有效签名$\sigma$，使得$lr.msg=m$和$SVf(pk,lr，\sigma )=1$，其中$CS$表示腐化的符号集。

TS-SUF-3仅为$lr$额外指定一个函数$lr.PP$的方案定义，该函数将每个$i\in lr.SS$映射到由签名者$i$生成的预处理令牌。
TS-SUF-3保证攻击者可以为$m$生成有效签名$\sigma$，除了TS-SUF-2的条件外，它还必须从每个诚实的签名者$i$接收到部分签名，使得签名者$i$为$lr$诚实地生成$lr.PP(i)$。

其中TS-SUF-2 game包含除虚线框外的所有内容，TS-SUF-3 Game包含除实线框外的所有内容

安全性原文的描述：（包括TS-SUF-2 Security of FROST2，TS-SUF-3 Security of FROST1）
https://link.springer.com/chapter/10.1007/978-3-031-15985-5_18

FROST1/2-H

同理MuSig2-H，本方案与原方案的区别仅在于使用LHF代替具体的离散对数计算，参数的取值为更泛化的域$\mathcal{D}$代替具体的${\mathbb{Z}}_p$。以及，除了一般的变换，还需要选择一个注入$x_{(\cdot )}:[n]\to \mathcal{S}$。
$x_{(\cdot )}$的选择可以是任意的，对应一组指标$S\subseteq [n],i\in S$的拉格朗日系数定义为

FROST2是一个优化版本，减少了签名和验证所需的幂次次数从$|lr.SS|$到1。
领导者状态$s{t}_0$包含每个服务器$i$的一组$curP{P}_i$，表示服务器$i$生成的尚未在签名请求中使用的令牌集。服务器$i$的状态$s{t}_i$包含一个函数$mapPP$，它将每个令牌$pp$映射到用于生成$pp$的随机性，如果$pp$尚未由服务器$i$生成或已在签名请求中使用，则$s{t}_i.mapPP(pp)=\perp$。

原方案：

原文中对系数的定义：
Lagrange coefficient ${\lambda }_i^{lr.SS}$定义：对于任何$S\subseteq [1,..ns]$

$CompPar$算法是在签名时使用的计算参数$R,c，\{d_i{\}}_{i\in lr.SS}$的辅助算法。FROST1和FROST2的区别在于$CompPar$中$d_i$的计算方式。在FROST1中，每个$d_i$是每个服务器$i$的不同哈希值，而在FROST2中，$d_i$是所有服务器的相同哈希值。

实例化

基于DLP

根据[30]实例化，从group generation algorithm$GGen$实例化一个线性哈希函数族GLHF，如下所示：

• 输入$1^{\kappa },PGen$运行$GGen(1^{\kappa })$并得到$(\mathbb{G},p,g)$，均匀采样一个$Z\in \mathbb{G}$并返回$\kappa \leftarrow (\mathbb{G},p,g,Z)$
• 给定$\kappa$，定义$\mathcal{S}:={\mathbb{Z}}_p,\mathcal{D}:={\mathbb{Z}}_p^2,\mathcal{R}:=\mathbb{G}$。同时，对于任何$(x_1,x_2)\in {\mathbb{Z}}_p^2$，定义$F(x_1,x_2):=g^{x_1}{Z}^{x_2}$。
• 对$\mathcal{D}$的运算定义如下。对于任何$(x_1,y_1),(x_2,y_2)\in \mathcal{D},s\in \mathcal{S}$，定义$(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2),s\cdot (x_1,y_1)=(s{x}_1,s{y}_1)$
• 对$\mathcal{R}$的运算定义如下。对于任何$x_1,x_2\in \mathcal{R},s\in \mathcal{S}$，定义$x_1+x_2=x_1{x}_2,s\cdot x_1=x_1^s$，其中$x_1{x}_2,x_1^s$都是group $\mathbb{G}$操作

定理表明，GLHF是一个线性哈希函数族，并且GLHF的抗碰撞性由离散对数假设隐含。
（也就是说所有的实例化只需要给出满足条件的线性哈希函数族）

要实例化MuSig2-H、FROST1-H和FROST2-H，设置参数:

基于RSA

要从RSA问题实例化线性哈希函数族，我们必须使用一个较弱的概念，称为弱线性哈希函数，它与线性哈希函数相同，只是$\mathcal{S}$只需要是一个环而不是一个field。正式地，我们从RSA参数生成算法RGen构造一个弱线性哈希函数族RLHF，如下所示

• 输入$1^{\kappa },PGen$运行$RGen(1^{\kappa })$并得到$(N,e)$，均匀采样一个$w\in {\mathbb{Z}}_N^{\ast }$并返回$par\leftarrow (N,e,w)$
• 给定$par$，定义$\mathcal{S}:=\mathbb{Z},\mathcal{D}:={\mathbb{Z}}_e\times {\mathbb{Z}}_N^{\ast },\mathcal{R}:={\mathbb{Z}}_N^{\ast }$。同时，对于任何$(a,x)\in {\mathbb{Z}}_e\times {\mathbb{Z}}_N^{\ast }$，定义$F(a,x):=w^a{x}^e\in {\mathbb{Z}}_N^{\ast }$。
• 对$\mathcal{D}$的运算定义如下。对于任何$(a_1,x_1),(a_2,x_2)\in \mathcal{D},s\in \mathcal{S}$，定义$(a_1,x_1)+(a_2,x_2)=(a_1+a_2,x_1{x}_2{w}^{\lfloor (a_1+a_2)/e\rfloor }),s\cdot (a_1,x_1)=(s{a}_1,x_1^s{w}^{\lfloor s{a}_1/e\rfloor })$，其中$a_1+a_2,s{a}_1$是在${\mathbb{Z}}_e$上计算的。
• 对$\mathcal{R}$的运算定义如下。对于任何$x_1,x_2\in \mathcal{R},s\in \mathcal{S}$，定义$x_1+x_2=x_1{x}_2,s\cdot x_1=x_1^s$，其中$x_1{x}_2,x_1^s$分别是${\mathbb{Z}}_N^{\ast }$上的乘法运算和指数运算。

前面的实例化类似于[30]中的实例化。唯一的区别是，我们将S设为Z，是为了使D和R都成为S模块。
https://link.springer.com/chapter/10.1007/978-3-030-17659-4_12

来看看原文是怎么定义的：
一个module由两个集合$\mathcal{S}$和$\mathcal{M}$指定，其中$\mathcal{S}$是一个具有乘法单位元素$1_{\mathcal{S}}$的环，$⟨\mathcal{M},+,0⟩$是一个加法阿贝尔群，一个映射$\cdot :\mathcal{S}\times \mathcal{M}\to \mathcal{M}$，即，对于所有$r,s\in \mathcal{S},x,y\in \mathcal{M}$，有（1）$r\cdot (x+y)=r\cdot x+r\cdot y$（2）$(r+s)\cdot x=r\cdot x+s\cdot x$（3）$(rs)\cdot x=r\cdot (s\cdot x)$（4）$1_S\cdot x=x$
线性函数族的语法。


实例：Okamoto-Guillou-Quisquater.