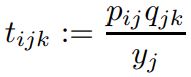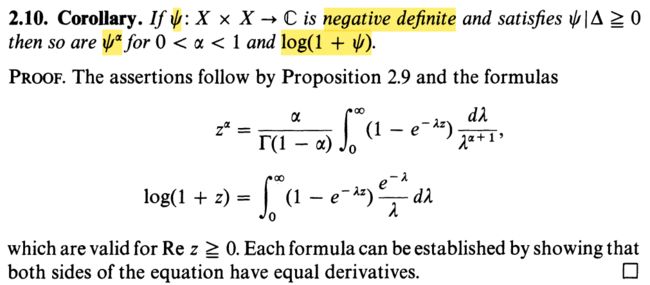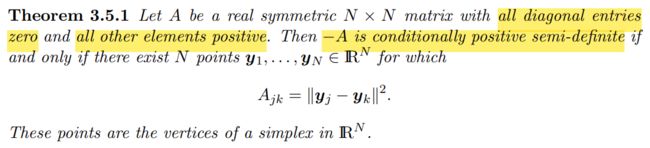OT1：Sinkhorn Distances: Lightspeed Computation of Optimal Transport

前言

为学习最优传输问题（Optimal Transport），拜读了博客《最优运输（Optimal Transfort）：从理论到填补的应用》，博文里简要介绍了三篇经典论文：

• Sinkhorn Distances: Lightspeed Computation of Optimal Transport $\Rightarrow$ 博文
• Wasserstein Generative Adversarial Networks $\Rightarrow$ 博文
• Missing Data Imputation using Optimal Transport $\Rightarrow$ 博文

本系列博文打算精读之，下面是第一篇。认知有限，有不理解之处，也可能有理解不当或错误之处，请读者多多指教。

Abstract

OT Distance 是什么以及有什么用途就不说了，上面的博文以及我其他的一些博文有讲。这段 Abstract 的四种颜色标记分别表示：

• 黄色，计算 OT 距离涉及的线性规划求解复杂度很高，一旦概率向量的维度超过几百，则开销就大到不可接受；
• 绿色，作者提出从最大熵的角度看 OT 问题，产生新的 OT 距离；
• 蓝色，具体做法：用熵正则项平滑经典 OT 问题，性质：加上熵正则项后，最优解依然是一个距离，且可以用 Sinkhorn’s Matrix Scaling Algorithm 以几个数量级的更快速度求解；
• 红色，作者为验证新 OT 距离的有效性，在 MNIST 数据集上进行了分类实验。

1 Introduction

P1 > 在统计机器学习中，有一些衡量概率分布差异的信息散度（information divergences），包括 Hellinger, ${\chi }^2$, total variation or Kullback-Leibler divergences；而 OT 距离（也称“推土距离 EMD”）在比较概率方面提供了更强的几何性。【?】

P2 > 但 OT 问题求解复杂度相当高，包括网络单纯形法和内点法在内的求解方法复杂度最低也要 $O(d^{3}log(d))$。

P3 > 尽管有 embedding 之类的简化求解方案，但实用性欠佳；在高维数据盛行的时代，较高的计算成本甚至使 OT 受到了质疑。

P4 > 和 Abstract 中的绿色和蓝色一样，更详细了一点：熵正则化使 OT 问题转化为严格凸优化，Sinkhorn’s Matrix Scaling Algorithm 是不动点迭代（fixed point iteration），具有线性收敛性，具体是实现仅需 matrix-matrix products。

P4 中 “two histograms of dimension $d$ or two point clouds each of size $d$”，看到 “point clouds” 想起当初《Notes on Optimal Transport (笔记)》中的数据点插入问题，当时对 “数据点怎么能最优传输呢？” 迷惑不解，苦苦思考才弄懂。现在看点云，是否还是：
“那我们就给他恢复这种概念，把这些点想象成一堆堆的小土堆，如何以最小的代价将 “土堆集” set1 变成 “土堆集” set2？点与点之间运送的土量就是连接强度。既然同一集合中小土堆都一样（没有谁是特别的），那它们的土量都是一样的。设土量为 1，set1 中有 n 个土堆，每个土堆的土量为 1/n，set2 中有 m 个土堆，每个土堆的土量为 1/m，运送土的代价就是两个土堆之间的距离。”？

2 Reminders on Optimal Transport

本节简单介绍什么是最优传输。博客《最优运输（Optimal Transfort）：从理论到填补的应用》以及《Notes on Optimal Transport》有较为详细的介绍，尤其后者借助糕点分配的故事讲解得较为生动，我已将其翻译为中文并加以注释。

这里需要说的是一个概念：Transport Polytope
翻译成中文就是传输多面体，怎么理解呢？从文中的意思看，它是 a Set of Joint Probabilities，一个联合分布的集合，写为

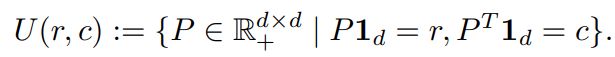
也即它包含了所有可能的传输方案。可是它为什么叫多面体？猜想可能限制条件 $P{1}_d=\mathbf{r},P^{⊺}{1}_d=\mathbf{c}$ 在空间中的几何形态类似多面体吧，想想三维空间中的线面，到高维空间就是多面体了。《Convex Optimization - Polyhedral Set》中有定义，同时也定义了距离矩阵集合为什么叫 cone？

现将其搬运过来：

A set in ${\mathbb{R}}^n$ is said to be polyhedral if it is the intersection of a finite number of closed half spaces, i.e., $$S=\{\mathbf{x}\in {\mathbb{R}}^n:{\mathbf{p}}_i^{⊺}\mathbf{x}\le {\alpha }_i,i=1,2,\dots ,n\}$$
For example,$\{\mathbf{x}\in {\mathbb{R}}^n:A_i^{⊺}X=\mathbf{b}\};\{\mathbf{x}\in {\mathbb{R}}^n:A_i^{⊺}X\le \mathbf{b}\},\{\mathbf{x}\in {\mathbb{R}}^n:A_i^{⊺}X\ge \mathbf{b}\}$
Polyhedral Cone A set in ${\mathbb{R}}^n$ is said to be polyhedral cone if it is the intersection of a finite number of half spaces that contain the origin, i.e., $$S=\{\mathbf{x}\in {\mathbb{R}}^n:{\mathbf{p}}_i^{⊺}\mathbf{x}\le 0,i=1,2,\dots ,n\}$$ 其包含原点，对数乘封闭，下图是维基百科给出的形状：

应该是圆锥吧。

本节还有个问题：

这里说只要 $M$ 是个距离矩阵，那么 OT 解也是个距离。如果 $M$ 不是距离矩阵呢？就如同糕点故事中的偏好矩阵，$d_M(\mathbf{r},\mathbf{c})$ 还是距离吗？答：从第三节末尾对 “$d_M(\mathbf{r},\mathbf{c})$ 是距离” 证明来看，用到了不等式 $m_{ik}\le m_{ij}+m_{jk}$，那么应该是以 “$M$ 是个距离矩阵” 为前提的。

3 Sinkhorn Distances: Optimal Transport with Entropic Constraints

这一节给出限制联合分布熵的 OT 问题，作者想说他是在遵循最大熵原则（maximum-entropy principle），以及在限制熵以后，OT 解依然保持着度量的性质。用到了有关熵的知识，如果这一块比较欠缺，则可以参考我的博文《由一个熵不等式引发的数学调研》。

3.1 Entropic Constraints on Joint Probabilities

首先要说明的是，作者是如何限制联合分布熵的，先看下面两个不等式

第一个是天然成立的，第二个是作者添加的熵限制，组合起来看，有 $$h(\mathbf{r})+h(\mathbf{c})-\alpha \le h(P)\le h(\mathbf{r})+h(\mathbf{c})$$ 熵被限制在了一个长度为 $\alpha$ 的区间内。那么如何理解这个熵限制呢？从 $I(\mathbf{r}\Vert \mathbf{c})=KL(P\Vert \mathbf{r}{\mathbf{c}}^{⊺})\le \alpha$ 的角度来看，他是想让 $\mathbf{r}$ 和 $\mathbf{c}$ 的相关性少一点，也即使 $P$ 更趋于均匀。限制熵的原因将在第四节说明。

限制 $P$ 的熵之后，所得的最优传输解就叫 Sinkhorn Distance：

本节也给出了一个限制熵的原因：最大熵原则。但在我看来，这并不能成为限制熵的理由，因为不限制熵时算出的最优解是实实在在地比限制熵的情况下算出的解要小（即代价最小）。来看一看作者说了什么吧。

OT 的最优解往往在多面体 $U(\mathbf{r},\mathbf{c})$ 的一个顶点上，这个很好理解，我在《Notes on Optimal Transport (笔记)》文中的 “问题思考” 部分给出了解释。Such a vertex is a sparse $d\times d$ matrix with only up to $2d-1$ non-zero elements. 这个稀疏性从感觉上可以知道，在顶点上嘛，至于为什么是 “up to $2d-1$ non-zero elements”，我不知道，有人知道的请留言。不过从《笔记》中可以看出，确实是非常稀疏的。

3.2 Metric Properties of Sinkhorn Distances

这一小节讲述限制 $P$ 的熵之后，Sinkhorn Distances 的度量性质。首先是两个特殊情况：

（1）$\alpha =0$

当 $\alpha =0$ 时，$h(\mathbf{r})+h(\mathbf{c})-\alpha \le h(P)\le h(\mathbf{r})+h(\mathbf{c})$ 的区间长度变为 $0$，$h(P)=h(\mathbf{r})+h(\mathbf{c})$ 或者说 $I(\mathbf{r}\Vert \mathbf{c})=KL(P\Vert \mathbf{r}{\mathbf{c}}^{⊺})=0$，则 $U_{\alpha }(\mathbf{r},\mathbf{c})=\{P=\mathbf{r}{\mathbf{c}}^{⊺}\}$。

初看 “has a closed form”，懵逼了，啥是 “has a closed form”？维基百科中有定义

而中文维基百科中查到 “闭式解” 就是我们通常说的 “解析解”。这个 “closed form” 就是包含有限次常见运算的表达式，不包括极限、积分等。
因为现在 $P=\mathbf{r}{\mathbf{c}}^{⊺}$，本质上可行解 $U_0(\mathbf{r},\mathbf{c})=\{P=\mathbf{r}{\mathbf{c}}^{⊺}\}$ 已不是一个集合，而是一个点，此时 $$d_{M,0}(\mathbf{r},\mathbf{c})=⟨\mathbf{r}{\mathbf{c}}^{⊺},M⟩={\mathbf{r}}^{⊺}M\mathbf{c}$$ 这不再是一个要求解的 problem，而是一个解析表达式，即 closed form。

至于为什么又 “becomes a negative definite kernel”？更让人匪夷所思。回想 SVM 中的正定核：$k(\mathbf{x},\mathbf{y})$，一组向量 $\{{\mathbf{x}}_i{\}}_1^n$ 用 $k(\mathbf{x},\mathbf{y})$ 计算 “高维内积” 得到的 Gram 矩阵半正定，则 $k(\mathbf{x},\mathbf{y})$ 为正定核。那如今 $d_{M,0}(\mathbf{r},\mathbf{c})=⟨\mathbf{r}{\mathbf{c}}^{⊺},M⟩$ 怎么成了负定核？是给定一组概率单纯形 $\{{\mathbf{p}}_i{\}}_1^n$，由其计算的 Gram 矩阵半负定吗？

先看后面的说法，“one assumes that $M$ is itself a negative definite distance, or equivalently a Euclidean distance matrix，意思是说 $M$ 是一个负定距离，“等价地一个欧式距离矩阵”。暂时只能理解为：欧式距离是一个负定距离，欧氏距离矩阵是半负定矩阵 。可是这不对啊，当场就能推翻：假设有点 $x_1=1,x_2=2$，那么欧式距离矩阵为 $M=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$，此时二次型 $f(x,y)=\left[\begin{array}{c}xy\end{array}\right]M\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}xy\end{array}\right]\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=2xy$，肯定不是恒小于等于 $0$ 的嘛。搜索维基百科又搜不到正负定距离的概念，只能搜到矩阵正定负定的定义和正定核的概念。既然本段里说 $d_{M,\alpha }(\mathbf{r},\mathbf{c})$ 是负定核，就当欧氏距离 $d(\mathbf{x},\mathbf{y})=\Vert \mathbf{x}-\mathbf{y}\Vert$ 是个负定核，可是现在欧式距离矩阵明明不负定哎！搜谷歌吧，有一个网页中提出了这个问题

这个人也是困惑于为何欧氏距离是负定，他能证明欧式距离是条件负定的：${\sum }_i{r}_i=0$，即刚才的 $f(x,y)=2xy$ 中 $x+y=0$，如此看来就通了。

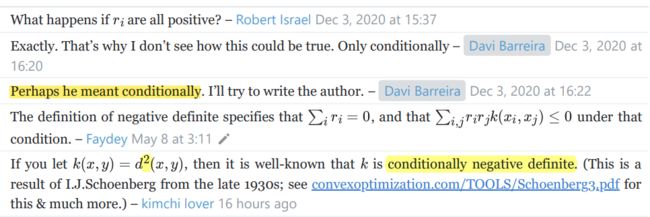
问题下面的回答也说 “作者可能是指条件负定”。对于欧氏距离矩阵的条件负定性此处不给出证明了（因为我不会），不过我编程试验了，确实是条件负定的。而且，经试验，如果 $M$ 是条件负定的话，$d_{M,0}(\mathbf{r},\mathbf{c})=⟨\mathbf{r}{\mathbf{c}}^{⊺},M⟩$ 也是条件负定的。【读到论文末，在其补充材料处发现了 $d_{M,0}(\mathbf{r},\mathbf{c})$ 的负定证明， 此过程亦可证明欧氏距离 $M$ 的条件负定。此博文末予以证明。】

扯了这么多，作者扯负定干嘛？有什么卵用吗？也许他只是想说：当 $\alpha =0$ 时，如果 $M$ 是个距离矩阵，那么 $d_{M,\alpha }(\mathbf{r},\mathbf{c})=⟨\mathbf{r}{\mathbf{c}}^{⊺},M⟩$ 也是个距离。本来就是要证明 Sinkhorn Distance 是距离，不能少了 $\alpha =0$ 的情况。

问题在于，“条件负定矩阵” 和 “负定距离” 是不是等价的？如果是，那么作者扯这些正负定就有意义了，否则讲不通！

（2）$\alpha$ 足够大时

当 $\alpha$ 足够大时，它就不起作用了， Sinkhorn Distance 变回普通的 OT 距离。因为 $h(P)\ge \frac{1}{2}[h(\mathbf{r})+h(\mathbf{c})]$，这个可以通过上面的 FIGURE 2.2 直接观察得出。那么只要有 $\alpha \ge \frac{1}{2}[h(\mathbf{r})+h(\mathbf{c})]$，$\alpha$ 便不起作用了。给定 $\mathbf{r}$ 和 $\mathbf{c}$ 的维度 $n$，则有 $h(\mathbf{r})\le log(n)$，那么，当 $\alpha >log(n)$ 时，铁定不起作用，有 $U_{\alpha }(\mathbf{r},\mathbf{c})=U(\mathbf{r},\mathbf{c})$。

还是那个问题，扯正定负定干嘛？我现在有两个猜想：【不懂，也验证不了】

1. 是不是条件负定核就是距离矩阵？
2. 和下面的求解算法有关吗？【下面的求解算法并没有提正定负定的事!】

继续分析其度量性质

加了熵限制后，其不再满足 $d(x,y)\iff x=y$，例如，当 $\alpha =0$ 时，有 $$\begin{array}{rl}{d}_{M,0}(\mathbf{r},\mathbf{r})& ={\mathbf{r}}^{⊺}M\mathbf{r}\\ & =\sum _{ij}^n{r}_i{r}_j\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2\end{array}$$ 若有 $r_k\ne 0,r_l\ne 0,k\ne l$，则 $r_k{r}_l>0\&\&\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2>0$，必有 $d_{M,0}(\mathbf{r},\mathbf{r})>0$。作者通过 $1_{\mathbf{r}\ne \mathbf{c}}{d}_{M,\alpha }(\mathbf{r},\mathbf{c})$ 将 $d_{M,\alpha }(\mathbf{r},\mathbf{r})$ 乘以 $0$ 来恢复这种性质。

对称性是公式自带的，不论是 $⟨P,M⟩$，还是后面的熵限制 $h(P)\ge h(\mathbf{r})+h(\mathbf{c})-\alpha$，都是天然的对称。

三角不等式的证明

Computational Optimal Transport 一书中对基本的 p-Wasserstein distance 的三角不等式证明很详细，其用到了一个叫 gluing lemma 的东西：

大概意思就是：利用两个 Wasserstein 距离的解空间 $P\in U(\mathbf{a},\mathbf{b}),Q\in U(\mathbf{b},\mathbf{c})$ 构建出一个新的解空间 $S\stackrel{def.}{=}Pdiag(1/\tilde{b})Q\in U(\mathbf{a},\mathbf{c})$，即 $S{1}_n=\mathbf{a},S^{⊺}{1}_n=\mathbf{c}$。

有了这个耦合器，再利用闵可夫斯基不等式就能证明三角不等式了：

到了带熵限制的 Sinkhorn 距离，这个叫 gluing lemma 的耦合器也自然要带上熵限制的：

可以看到形式上基本是一模一样的，只是这里的解空间变成了 $U_{\alpha }$，至于三角不等式的证明，就更没有什么差别了。所以，要注意的是，这个新建的 $S$ 到底是不是 $\in U_{\alpha }$ 的？即：$$h(S)\ge h(\mathbf{x})+h(\mathbf{z})-\alpha$$ 是否成立？

这是文末补充材料给出的证明，根据

可构造出一个马尔科夫链 $X\to Y\to Z$，链状之后，应该是有个定理啥的：链中，挨得更近的变量之间互信息更大，因为依赖更大。所以就有了后面的不等式，进而的出：$h(S)\ge h(X)+h(Z)-\alpha$。

Computing Regularized Transport with Sinkhorn’s Algorithm

以正则项的方式限制熵，系数 $-\frac{1}{\lambda }$ 会使 $h(P)$ 变大，且 $\lambda \in (0,\infty )$ 使主目标 $⟨P,M⟩$ 和正则项 $-\frac{1}{\lambda }h(P)$ 之间分配权重。当 $\lambda \to 0$ 时，系数会无穷大，致使目标函数只考虑熵项，而忽略主目标，自然就对应了 $\alpha =0$；当 $\lambda \to \infty$ 时，系数为 0，致使目标函数只考虑主目标，而忽略熵项，恢复原本的瓦斯距离，即上文的 $\alpha$ “足够大”。故而，each $\alpha$ corresponds a $\lambda \in [0,\infty ]$。

$d_M,d_{M,\alpha },d_M^{\lambda }$ 的示意图，从上到下吧，看一看。

箭头 $M$ 应该是指 $⟨P,M⟩$ 关于 $P$ 的梯度，是代价降低的反方向，绿红蓝三条虚线大概是代价等高线吧，这解释了为何 $P^{\star }$ 总会出现在 Polytope $U(\mathbf{r},\mathbf{c})$ 的角上，我在博文 Notes on Optimal Transport (笔记) 中已经从线性规划的角度讲述了可行域 $U(\mathbf{r},\mathbf{c})$ 的样子，以及为什么最优解会出现在多边形的角落上。

那么 $U_{\alpha }$ 是以 $\mathbf{r}{\mathbf{c}}^{⊺}$ 为中心的 ball 吗？我们来算一算，$h(P)$ 的范围是：$$h(\mathbf{r})+h(\mathbf{c})-\alpha \le h(P)\le h(\mathbf{r})+h(\mathbf{c})$$ 注意，$\mathbf{r},\mathbf{c}$ 是给定的，那 $h(\mathbf{r})+h(\mathbf{c})$ 自然是确定的，再给定 $\alpha$，则 $h(P)$ 就有一个固定的范围。前面讨论过，$h(P)$ 有一个自然的上下限 $\frac{1}{2}(h(\mathbf{r})+h(\mathbf{c}))\le h(P)\le h(\mathbf{r})+h(\mathbf{c})$，$h(\mathbf{r})$ 和 $h(\mathbf{c})$ 也有范围 $[0,logn]$，那么 $h(\mathbf{r})+h(\mathbf{c})\in [0,2logn]$。

当取 $\alpha =0$， 即 $h(P)=h(\mathbf{r})+h(\mathbf{c})$ 时，就是中心点 $P=\mathbf{r}{\mathbf{c}}^{⊺}$，随着 $\alpha$ 增大，大到失去作用时，就是铺满整个 Polytope $U(\mathbf{r},\mathbf{c})$。当取一个起作用的 $\alpha$ 时，令 $t=h(\mathbf{r})+h(\mathbf{c})-\alpha$，则 $$h(P)=-\sum _{ij}{P}_{ij}log{P}_{ij}\ge t$$ 它的边界是 $-{\sum }_{ij}{P}_{ij}log{P}_{ij}=t$，不是线性的，也不是二次的，所以它应该是个超曲面。所以，途中画成曲线围成的范围是合理的。但是不是 ball 就不知道了！

随着 $\lambda$ 的增大，熵限制越来越松弛，最优解沿着从 $\mathbf{r}{\mathbf{c}}^{⊺}$ 到 $P^{\star }$ 的曲线滑动，也很形象。

Computing $d_M^{\lambda }$ with Matrix Scaling Algorithms

这个引理意思是说：对偶解 $P^{\lambda }$ 是唯一的，且形式为 $P^{\lambda }=diag(\mathbf{u})Kdiag(\mathbf{v})$，其中 $\mathbf{u}$ 和 $\mathbf{v}$ 是非负向量，且唯一地被乘子(应该是$\lambda$)确定。

这个结论来源于 Sinkhorn’s Theorem：

一个元素全部为正的方阵 $A$，有唯一的正对角矩阵 pair $(D_1,D_2)$ 使 $D_{1}A{D}_2$ 是 Doubly Stochastic Matrix，即行和列和都为 $1$ 的方阵 。

但是论文中有不一样的地方：$P^{\lambda }=diag(\mathbf{u})Kdiag(\mathbf{v})$ 并不是所谓的 Doubly Stochastic Matrix，它的行和等于 $\mathbf{r}$，列和等于 $\mathbf{c}$。这里是 $P^{\lambda }$ 唯一地属于 $U(\mathbf{r},\mathbf{c})$。然后就可以用 Sinkhorn’s fixed point iteration 进行求解了。咱就当它是个引理吧，Sinkhorn’s Theorem 咱不懂背后的原理，这里的变更版就更不懂了，记住这个结论吧。

来看 $p_{ij}=e^{-1/2-\lambda {\alpha }_i}{e}^{-\lambda m_{ij}}{e}^{-1/2-\lambda {\beta }_j}$，确实有 u = [ e − 1 / 2 − λ α 1 , e − 1 / 2 − λ α 2 , ⋯   , e − 1 / 2 − λ α n ] v = [ e − 1 / 2 − λ β 1 , e − 1 / 2 − λ β 2 , ⋯   , e − 1 / 2 − λ β n ] K = [ m 11 m 12 … m 1 n m 21 m 22 … m 2 n ⋮ ⋮ ⋱ ⋮ m n 1 m n 2 … m n n ] \begin{aligned} \bm{u} &= [e^{-1/2 - \lambda \alpha_1}, e^{-1/2 - \lambda \alpha_2}, \cdots, e^{-1/2 - \lambda \alpha_n}] \\ \bm{v} &= [e^{-1/2 - \lambda \beta_1}, e^{-1/2 - \lambda \beta_2}, \cdots, e^{-1/2 - \lambda \beta_n}] \\ K &= \begin{bmatrix} m_{11} & m_{12} & \dots & m_{1n} \\ m_{21} & m_{22} & \dots & m_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ m_{n1} & m_{n2} & \dots & m_{nn} \\ \end{bmatrix} \end{aligned} uvK​=[e−1/2−λα1​,e−1/2−λα2​,⋯,e−1/2−λαn​]=[e−1/2−λβ1​,e−1/2−λβ2​,⋯,e−1/2−λβn​]= ​m11​m21​⋮mn1​​m12​m22​⋮mn2​​……⋱…​m1n​m2n​⋮mnn​​ ​​ 知识有限，只能理解到这了，后面的计算是很简单的，这里有更简单的 python 代码。

问题在于：通篇都是按 $M$ 是个对称的距离矩阵讲述与证明的，而现实中，$\mathbf{r}$ 和 $\mathbf{c}$ 不同维的情况很多，代价矩阵 $M$ 也未必是对称的负定距离矩阵，这种计算的合理性还在吗？不过根据糕点实验，这一切似乎都照常进行。最要紧的是，我们并不知道作者是如何做实验的。

5. 实验

5.1 实验过程

在这里看到了核，终于明白作者想做什么实验了。这个 $e^{-d/t}$ 很像高斯核 $e^{-\frac{\Vert \mathbf{x}-\mathbf{y}{\Vert }^2}{2{\sigma }^2}}$ 和拉普拉斯核 $e^{-\frac{\Vert \mathbf{x}-\mathbf{y}\Vert }{\sigma }}$，相似之处在于，它们都是距离的指数函数。这也是个收获：可能距离函数的指数，都能作为核函数吧。$t$ 根据距离值域的百分位 $q_s(d)$ 进行选择。【关于这个 $t$ 的讲究，它和高斯核中的 $\sigma$ 一样，《支持向量机通俗导论》中说，$\sigma$ 越大，拟合能力越弱，越小拟合能力越强，调节它可以在欠拟合和过拟合之间平衡】

有了核函数，就可以利用 SVM 进行分类了：

作者说可以用库 $Libsvm$ 跑 $svm$ 进行多分类。多分类策略是 OvO，不过 MNIST 有 10 个类别，那么就需要 $10\ast 9/2=45$ 个二分类器，开销还是蛮大的。

果然，作者还尝试了高斯核，高斯核中的距离函数是平方欧式距离。

这个独立核，就是上文的 $e^{-t{d}_{M,0}}=e^{-t⟨\mathbf{r}{\mathbf{c}}^{⊺},M⟩}$，那么这就是实验的一个特例 $\alpha =0$，即 $\lambda \to 0$ 时的情况。而 $[m_{ij}^a]$ 中的 $a$ 只是一种超参数调整。但我觉得这没意义吧，均匀分布的 Sinkhorn 距离，估计都没什么距离区分性！

5.2 实验结果

作者给出的 matlab 代码确实实现了 Sinkhorn 算法，但是真正的实验代码并未提供，故而实验结果真假难辨，就不必看了。后来在 GitHub 搜到了一份印度人写的复现代码，有些许不一样，也不能直接运行！太难了！她计算了图片之间的 Sinkhorn Distance 之后，直接将距离矩阵带上核范数输入到了一个叫 fitcecoc 的函数：

官方文档说这个函数训练一个 ECOC 多分类器，所用的二元分类器是 SVM，第一个参数是数据特征，第二个是类别。这样的话，作者说的核 $e^{-d/t}$ 如何体现呢？

结语

到最后，也没看到强调正定负定有什么用，这个让人头疼的问题。如果非要找出个用处，大概是 SVM 中的核函数 $e^{-d/t}$ 要求 $d$ 是个距离，而 “负定距离” 和 “条件负定矩阵” 的概念可以保证 Sinkhorn Distance 能用于核函数。【这只是猜想，知识有限，不能明确!】

---

Update1：欧式距离的条件负定证明

---

给定一组向量 ${\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_i,\dots ,{\mathbf{x}}_n\in {\mathbb{R}}^d$，其欧式距离矩阵为 $M$，其元素 $m_{ij}=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2$，$\forall \mathbf{r}\in {\mathbb{R}}^n$ $$\begin{array}{rl}{\mathbf{r}}^{⊺}M\mathbf{r}& =\sum _{ij}^n{r}_i{r}_j\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2\\ & =\sum _{ij}^n{r}_i{r}_j(\Vert {\mathbf{x}}_i{\Vert }^2+\Vert {\mathbf{x}}_j{\Vert }^2-2{\mathbf{x}}_i^{⊺}{\mathbf{x}}_j)\\ & =\sum _{ij}^n{r}_i{r}_j\Vert {\mathbf{x}}_i{\Vert }^2+\sum _{ij}^n{r}_i{r}_j\Vert {\mathbf{x}}_j{\Vert }^2-2\sum _{ij}^n{r}_i{r}_j{\mathbf{x}}_i^{⊺}{\mathbf{x}}_j\\ & =\sum _j^n{r}_j\sum _i^n{r}_i\Vert {\mathbf{x}}_i{\Vert }^2+\sum _i^n{r}_i\sum _j^n{r}_j\Vert {\mathbf{x}}_j{\Vert }^2-2\sum _{ij}^n{r}_i{r}_j{\mathbf{x}}_i^{⊺}{\mathbf{x}}_j\end{array}$$ 到这，其实没法进行下去了。经过编程验证，如果不对 $\mathbf{r}$ 加以限制为 ${\sum }_i{r}_i=0$，${\mathbf{r}}^{⊺}M\mathbf{r}$ 是有正有负的，即不定。现假定 ${\sum }_i{r}_i=0$：$$\begin{array}{r}{\mathbf{r}}^{⊺}M\mathbf{r}=-2\sum _{ij}^n{r}_i{r}_j{\mathbf{x}}_i^{⊺}{\mathbf{x}}_j\le 0\end{array}$$ 就得到了条件负定。

不过这里是欧氏距离的平方 $d^2(\mathbf{x},\mathbf{y})=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2$，对于 $d(\mathbf{x},\mathbf{y})=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert$，我还没找到证明的方法，虽然能验证它是条件负定的。文中脚注说：

也即 $d^t(\mathbf{x},\mathbf{y})=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^t,\forall t\in (0,2]$ 是条件负定的。故欧式距离是条件负定的。至于为什么是这样，Berg1984 $\S 3.2.10$ 中这样写道：

全然不懂，也不打算去深究了，暂且就这么认为。

---

Update2：$U_{\alpha }(\mathbf{r},\mathbf{c})$ 的凸性证明

---

凸集，用数学语言写就是：$$\begin{array}{rl}& \forall P^{(1)},P^{(2)}\in U_{\alpha }(\mathbf{r},\mathbf{c})\\ \Rightarrow & \forall t\in [0,1],P=t{P}^{(1)}+(1-t)P^{(2)}\in U_{\alpha }(\mathbf{r},\mathbf{c})\end{array}$$ 先看看 $U(\mathbf{r},\mathbf{c})$ 凸不凸吧 $$\begin{array}{rl}P{1}_m& =[t{P}^{(1)}+(1-t)P^{(2)}]1_m\\ & =t{P}^{(1)}{1}_m+(1-t)P^{(2)}{1}_m\\ & =t\mathbf{r}+(1-t)\mathbf{r}\\ & =\mathbf{r}\end{array}$$ 同理 $P^{⊺}{1}_n=\mathbf{c}$，故 $P\in U(\mathbf{r},\mathbf{c})$，凸！下一步，我们要导出 $$\begin{array}{rl}h(P)& =h(t{P}^{(1)}+(1-t)P^{(2)})\\ & \ge th(P^{(1)})+(1-t)h(P^{(2)})①\\ & \ge t[h(\mathbf{r})+h(\mathbf{c})-\alpha ]+(1-t)[h(\mathbf{r})+h(\mathbf{c})-\alpha ]\\ & =h(\mathbf{r})+h(\mathbf{c})-\alpha \\ \Rightarrow P& \in U_{\alpha }(\mathbf{r},\mathbf{c})\end{array}$$ 其中 $①$ 来源于熵函数的凹性。故 $U_{\alpha }(\mathbf{r},\mathbf{c})$ 是凸的。

---

Update3：条件负定矩阵和距离矩阵的关系

---

其实从 Metric Properties of Sinkhorn Distances 一节中已经可以看出一些结论，只不过我在不明白怎么回事的情况下不愿意接受而已。先看看从论文中能得到什么。

这一句话中，negative definite distance 和 Euclidean distance matrix 是等价的。 从 “itself” 可知 negative definite distance 和 negative definite kernel 等价。

脚注说：对于 Euclidean distance matrix $M=[m_{ij}]=[\Vert {\phi }_i-{\phi }_j{\Vert }_2^2]$ 而言，矩阵 $[m_{ij}^t]$ 也是 Euclidean distance matrix，其中 $0<t<1$。

好家伙，这么说来，有以下概念是等价的：$$\begin{array}{rl}& negativedefinitekernel\\ \iff & negativedefinitedistance\\ \iff & Euclideandistancematrix\\ \iff & [\Vert {\phi }_i-{\phi }_j{\Vert }_2^t],t\in (0,2]\end{array}$$ Sinkhorn Distance 也是欧式距离矩阵？

再看这一段，$d_{M,0}$ 是一个 negative definite kernel，并且 $e^{-t{d}_{M,0}}$ 是 positive definite，其中 $t>0$。大致可猜想：如果 $d$ 是个负定核，那么 $e^{-td}$ 是 positive definite。

从这里可确定上面的猜想，只要 $d$ 是个距离、$t>0$，$e^{-d/t}$ 就是个核函数，作者用这个核去跑 SVM 了。

真不敢相信，负定核真的和距离函数是等价的。

Scattered Data Interpolation with Polynomial Precision and Conditionally Positive Definite Functions 中的一些定理引理让我相信了这个结论，虽然这里面并没有给出详细的证明，即使有估计也看不懂。