中缀表达式构建后缀表达式
中缀表达式构建后缀表达式
文章目录
- 中缀表达式构建后缀表达式
-
- 一、构造符号优先关系表
- 二、构造后缀表达式
一、构造符号优先关系表
首先,我们需要知道什么是优先函数。优先函数是一种用于表示算符优先关系的函数,它有两种形式:f 和 g。f(a) 表示在栈中的算符 a 的优先级,g(b) 表示在输入中的算符 b 的优先级。我们用一个二维数组 pfunc 来存储这两种函数的值,其中 pfunc[0][a] 表示 f(a),pfunc[1][b] 表示 g(b)。我们的目标是根据给定的优先关系表 pt 来计算出 pfunc 的值。
优先关系表
| isp\icp | + | - | * | / | ( | ) | # | d |
|---|---|---|---|---|---|---|---|---|
| + | > | > | < | < | < | > | > | < |
| - | > | > | < | < | < | > | > | < |
| * | > | > | > | > | < | > | > | < |
| / | > | > | > | > | < | > | > | < |
| ( | < | < | < | < | < | = | < | |
| ) | > | > | > | > | > | |||
| # | < | < | < | < | < | = | < | |
| d | > | > | > | > | > | > |
优先关系表 pt 是一个 n x n 的矩阵,其中 n 是算符的数量。pt[a][b] 表示算符 a 和 b 之间的优先关系,它有三种可能的值:-1,0,1。-1 表示 a < b,即 a 的优先级低于 b;0 表示 a = b,即 a 和 b 的优先级相同;1 表示 a > b,即 a 的优先级高于 b。例如,pt[0][2] = -1 表示第一个算符(假设是 +)的优先级低于第三个算符(假设是 *)。
如何根据 pt 来计算 pfunc 呢?在这里我们采用一种迭代的方法,每次更新 pfunc 的值,直到它不再变化或者达到最大的迭代次数。更新规则是:
- 如果
pt[a][b] = 1,即a > b,且pfunc[0][a] <= pfunc[1][b],即f(a) <= g(b),则将f(a)的值增加到g(b) + 1,即pfunc[0][a] = pfunc[1][b] + 1。这是为了保证a在栈中的优先级高于b在输入中的优先级,从而可以进行归约操作。 - 如果
pt[a][b] = -1,即a < b,且pfunc[0][a] >= pfunc[1][b],即f(a) >= g(b),则将g(b)的值增加到f(a) + 1,即pfunc[1][b] = pfunc[0][a] + 1。这是为了保证b在输入中的优先级高于a在栈中的优先级,从而可以进行移进操作。 - 如果
pt[a][b] = 0,即a = b,且pfunc[0][a] != pfunc[1][b],即f(a) != g(b),则将f(a)和g(b)的值统一为较大的那个,即pfunc[0][a] = pfunc[1][b] = max(pfunc[0][a], pfunc[1][b])。这是为了保证a和b的优先级相同,从而可以进行归约或移进操作。
#include 代码就是按照这个规则来更新 pfunc 的值的。我们用一个变量 flag 来标记是否发生了更新,如果没有更新,说明 pfunc 已经稳定,就可以返回它了。我们用一个变量 iter 来记录当前的迭代轮数,如果超过了限制的迭代轮数 limit_iter,我们就返回一个空的数组,表示无法计算出优先函数。
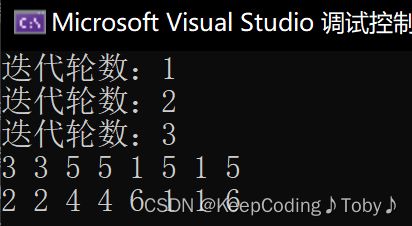
在 main 函数中,我们定义了一个符号优先关系表 pt,它是一个 8 x 8 的矩阵,表示了 8 个算符(+,-,*,/,(,),i,#)之间的优先关系。我们调用 getPriorityFunc 函数来计算优先函数,然后打印出结果。结果是一个 2 x 8 的矩阵,表示了 f 和 g 的值。例如,结果的第一行第一个元素是 3,表示 f(+) = 3,即 + 在栈中的优先级是 3。
结果如下:
| isp\icp | + | - | * | / | ( | ) | # | d |
|---|---|---|---|---|---|---|---|---|
| isp | 3 | 3 | 5 | 5 | 1 | 5 | 1 | 5 |
| icp | 2 | 2 | 4 | 4 | 6 | 1 | 1 | 6 |
二、构造后缀表达式
中缀表达式是我们日常使用的算术表达式,例如 a + b ∗ c a+b*c a+b∗c,它遵循运算符的优先级和结合性规则。后缀表达式是一种不需要括号的表达式,它将运算符放在操作数的后面,例如 a b c ∗ + abc*+ abc∗+,它遵循栈的先进后出原则。后缀表达式的优点是它可以方便地用计算机进行求值,而不需要考虑运算符的优先级和结合性。
为了将中缀表达式转换为后缀表达式,需要使用一个栈来存储运算符,以及两个映射表来记录运算符的栈内优先级和栈外优先级。栈内优先级是指运算符在栈顶时的优先级,栈外优先级是指运算符在表达式中时的优先级。我们还需要在表达式的两端添加一个特殊的符号 #,表示表达式的开始和结束。
转换的过程如下:
- 从左到右扫描表达式,遇到操作数则直接输出到后缀表达式,遇到运算符则进行下一步。
- 比较栈顶运算符的栈内优先级和当前运算符的栈外优先级,如果栈内优先级低于栈外优先级,则将当前运算符入栈,如果栈内优先级高于栈外优先级,则将栈顶运算符出栈并输出到后缀表达式,重复此步骤直到栈内优先级小于栈外优先级或栈为空。
- 如果栈内优先级等于栈外优先级,通常表示两个运算符是一对括号或者两个 #,则将栈顶运算符出栈,但不输出到后缀表达式,如果是一对 #,则表示转换结束,否则继续扫描表达式。
#include 代码中的类 infixToPostfix 封装了这个转换的过程,它有以下几个成员变量和函数:
infix:存储中缀表达式的字符串。postfix:存储后缀表达式的字符串。isp:存储运算符的栈内优先级的映射表,其中 # 的优先级为 1,( 的优先级为 1,) 的优先级为 5,+ 和 - 的优先级为 3,* 和 / 的优先级为 5,d 的优先级为 5(d 表示操作数)。icp:存储运算符的栈外优先级的映射表,其中 # 的优先级为 1,( 的优先级为 6,) 的优先级为 1,+ 和 - 的优先级为 2,* 和 / 的优先级为 4,d 的优先级为 6(d 表示操作数)。ispFunc:根据运算符返回其栈内优先级,如果运算符不存在于映射表中,则报错并退出。icpFunc:根据运算符返回其栈外优先级,如果运算符不存在于映射表中,则报错并退出。inToPost:执行转换的主要函数,它首先在中缀表达式的末尾添加一个 #,然后创建一个栈,从左到右扫描表达式,按照上述的规则进行入栈、出栈和输出操作,直到遇到两个 # 为止。getResult:调用in2post函数并返回后缀表达式的字符串。
代码中的 main 函数是用来测试的,它创建了一个infixToPostfix 的对象,并传入了中缀表达式 ( d + d ) ∗ d (d+d)*d (d+d)∗d,然后调用 getResult 函数并输出了后缀表达式 d d + d ∗ dd+d* dd+d∗。
下面是用表格表示的执行过程(如有错误欢迎指正,程序是对的):
| 步骤 | 当前字符 | 栈 | 后缀表达式 |
|---|---|---|---|
| 1 | ( |
# |
|
| 2 | ( |
#( |
|
| 3 | d |
#( |
d |
| 4 | + |
#( |
d |
| 5 | + |
#(+ |
d |
| 6 | d |
#(+ |
dd |
| 7 | ) |
#(+ |
dd |
| 8 | ) |
# |
dd+ |
| 9 | * |
# |
dd+ |
| 10 | * |
#* |
dd+ |
| 11 | d |
#* |
dd+d |
| 12 | # |
#* |
dd+d |
| 13 | # |
# |
dd+d* |