数据结构之树

一、树的遍历

1、深度优先遍历

①先序遍历：根左右

//先序遍历
public void preOrder(TreeNode treeNode){
    if(treeNode == null){
        return;
    }
    System.out.print(treeNode.getValue()+"  ");
    preOrder(treeNode.getLeftTreeNode());
    preOrder(treeNode.getRightTreeNode());
}

②中序遍历：左根右

//中序遍历
public void inOrder(TreeNode treeNode){
    if(treeNode == null){
        return;
    }
    inOrder(treeNode.getLeftTreeNode());
    System.out.print(treeNode.getValue()+"  ");
    inOrder(treeNode.getRightTreeNode());
}

③后序遍历：左右根

//后序遍历
public void afterOrder(TreeNode treeNode){
    if(treeNode == null){
        return;
    }
    afterOrder(treeNode.getLeftTreeNode());
    afterOrder(treeNode.getRightTreeNode());
    System.out.print(treeNode.getValue()+"  ");
}

2、广度优先遍历

//广度优先遍历
import java.util.LinkedList;
public void levelOrder(TreeNode treeNode){
    LinkedList queue = new LinkedList<>();

    if(treeNode!=null){
        queue.add(treeNode);
    }
    while(!queue.isEmpty()){
        treeNode = queue.remove();
        System.out.print(treeNode.getValue()+"  ");
        if(treeNode.getLeftTreeNode()!=null){
            queue.add(treeNode.getLeftTreeNode());
        }
        if(treeNode.getRightTreeNode()!=null){
            queue.add(treeNode.getRightTreeNode());
        }
    }
}

二、树的类型

1、完全二叉树：数据从上到下，从左到右依次排列

2、满二叉树：所有叶子节点都在同一层，且最后一层节点数为2^(n-1)

3、有序二叉树：左边节点值小于根节点值，右边节点值大于根节点

public class TreeNode {
    private int value;
    private TreeNode leftTreeNode;
    private TreeNode rightTreeNode;

    public TreeNode(int value) {
        super();
        this.value = value;
    }

    public TreeNode getRightTreeNode() {
        return rightTreeNode;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public void setLeftTreeNode(TreeNode leftTreeNode) {
        this.leftTreeNode = leftTreeNode;
    }

    public TreeNode getLeftTreeNode() {
        return leftTreeNode;
    }

    public void setRightTreeNode(TreeNode rightTreeNode) {
        this.rightTreeNode = rightTreeNode;
    }

    @Override
    public String toString() {
        return "TreeNode{" +
                "value=" + value +
                ", leftTreeNode=" + leftTreeNode +
                ", rightTreeNode=" + rightTreeNode +
                '}';
    }
}

①插入

public class BinaryTree {
    public TreeNode root;
    //插入
    public void insert(int value){
        //创建一个节点
        TreeNode node = new TreeNode(value);
        if(root==null){
            root=node;
            return;
        }
        //定义一个游标遍历整颗二叉树
        TreeNode index = root;
        //定义一个游标指向index前一个地址
        TreeNode pre = null;
        while(true){
            pre = index;
            if(index.getValue()value){
            //左边插入
            if(treeNode.getLeftTreeNode()==null){
                treeNode.setLeftTreeNode(node);
                return;
            }
            insertDG(treeNode.getLeftTreeNode(), value);
        }else{
            //右边插入
            if(treeNode.getRightTreeNode()==null){
                treeNode.setRightTreeNode(node);
                return;
            }
            insertDG(treeNode.getRightTreeNode(), value);
        }
    }
 }

②查找

//查找
public TreeNode find(int value){
    if(root == null){
        return null;
    }
    //定义index游标遍历树
    TreeNode index = root;
    while(index != null){
        if(index.getValue() == value){
            return index;
        }else if(index.getValue()>value){
            index = index.getLeftTreeNode();
        }else{
            index = index.getRightTreeNode();
        }
    }
    return null;
}

③删除

public void delete(int value, TreeNode treeNode){
    if(treeNode==null){
        System.out.println("空树");
        return;
    }
    //找目标节点
    TreeNode target = find(value);
    if(target==null){
        System.out.println("没有这个节点");
        return;
    }
    //找目标节点的父节点
    TreeNode parent = findParentNode(value, treeNode);
    //删除节点
    if(target.getLeftTreeNode()==null && target.getRightTreeNode()==null){
        //删除的是叶子节点
        //没有父节点
        if(parent==null){
            root = null;
        }else{
            //有父节点，确定目标节点是父节点的左孩子还是右孩子
            if(parent.getLeftTreeNode()!=null && parent.getLeftTreeNode().getValue()==value){
                //目标节点是父节点的左孩子
                parent.setLeftTreeNode(null);
            }else{
                //目标节点是父节点的右孩子
                parent.setRightTreeNode(null);
            }
        }
    }else if(target.getLeftTreeNode()!=null && target.getRightTreeNode()!=null){
        //删除有两棵子树的节点
        //找到目标节点右子树的最小值
        int min = findMin(target.getRightTreeNode());
        target.setValue(min);
    }else{
        //删除有一棵子树的节点
        if(parent==null){
            //没有父节点
            //确定目标节点有左孩子还是右孩子
            if(target.getLeftTreeNode()!=null){
                //目标节点有左孩子
                root = target.getLeftTreeNode();
            }else{
                //目标节点有右孩子
                root = target.getRightTreeNode();
            }
        }else{
            //有父节点
            //确定目标节点是父节点的左孩子还是右孩子
            if(parent.getLeftTreeNode()!=null && parent.getLeftTreeNode().getValue()==value) {
                //目标节点是父节点的左孩子
                if(target.getLeftTreeNode()!=null) {
                    //目标节点有左孩子
                    parent.setLeftTreeNode(target.getLeftTreeNode());
                }else {
                    //目标节点有右孩子
                    parent.setLeftTreeNode(target.getRightTreeNode());
                }

            }else {
                //目标节点是父节点的右孩子
                if(target.getLeftTreeNode()!=null) {
                    //目标节点有左孩子
                    parent.setRightTreeNode(target.getLeftTreeNode());
                }else {
                    //目标节点有右孩子
                    parent.setRightTreeNode(target.getRightTreeNode());
                }
            }
        }
    }
}

//查找节点的父节点
public TreeNode findParentNode(int value, TreeNode treeNode){
    if(treeNode == null){
        return null;
    }

    //判断当前节点是不是目标节点的父节点
    if(treeNode.getLeftTreeNode() != null && treeNode.getLeftTreeNode().getValue()==value){
        return treeNode;
    }else if(treeNode.getRightTreeNode() != null && treeNode.getRightTreeNode().getValue()==value){
        return treeNode;
    }else if(value>treeNode.getValue()){
        return findParentNode(value, treeNode.getRightTreeNode());
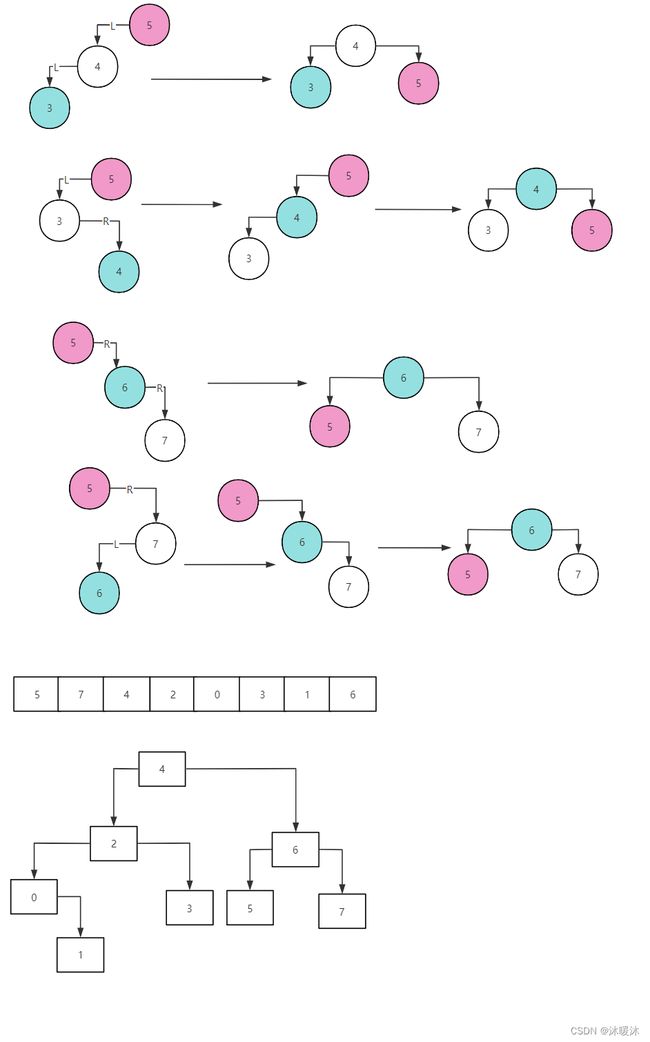
    }else if(value

4、平衡二叉树：左边节点值小于根节点值，右边节点值大于根节点，左右子树的高度差小于1

5、哈夫曼树：一种带权路径长度最短的二叉树，也称为最优二叉树。给定n个权值作为n个叶子节点，构造一颗二叉树，若树的带权路径长度达到最小，则这棵树称为哈夫曼树。树的带权路径长度等于根节点到所有叶子节点的路径长度与叶子节点权值乘积的总和。

6、多叉树：一个节点上可以有多个叉

B树：一个节点包含多个key-value值，只需要找到key就能找到value，多用于磁盘，红黑树内存最优

如图为五阶B树

M阶B树，每个节点最多有M-1个key，并且key值以升序排列，每个节点最多能有M个子节点

B+树：①非叶子节点仅具有索引作用，也就是非叶子节点只能存key值，不存value值；在内存相同的情况下，能存放更多的key值

②所有叶子节点构成一个有序链表，想要遍历树只需要一次线性遍历叶子节点即可，数据库中常用，key主键，value存储数据地址

如图为五阶B+树