单变量微积分笔记——积分的应用
本文内容对应我的博客中微积分笔记总目录下的第四章,积分的应用。
4. 积分的应用
4.1 平均值和加权平均值(Averages and Weighted Averages)
连续平均值的定义:
Continuous Average = 1 b − a ∫ a b f ( x ) d x \text{Continuous Average}=\frac{1}{b-a}\int_a^bf(x)dx Continuous Average=b−a1∫abf(x)dx
注意,平均值与选择的变量有关,比如求半圆高度的平均值,对 x x x轴和对圆心角 θ \theta θ会算出不同的结果,这是因为,对 x x x轴而言,分母是半圆的直径,而对于圆心角 θ \theta θ而言,分母则是半圆的周长。
加权平均值的定义:
Weighted Average = ∫ a b f ( x ) w ( x ) d x ∫ a b w ( x ) d x \text{Weighted Average}=\frac{\int_a^bf(x)w(x)dx}{\int_a^bw(x)dx} Weighted Average=∫abw(x)dx∫abf(x)w(x)dx
加权平均值在概率问题中非常常见。
4.2 求两条曲线包围下的面积
如下图所示,
我们要求的面积为蓝色区域,除此之外,我们还需要知道两条曲线的交点的坐标。之后我们可以得到,
Area = ∫ a b ( f ( x ) − g ( x ) ) ⎵ Height d x ⎵ B a s e \text{Area}=\int_a^b\underbrace{(f(x)-g(x))}_{\text{Height}}\underbrace{dx}_{Base} Area=∫abHeight (f(x)−g(x))Base dx
在具体情况中,一定要选好哪个变量是自变量,有一些情况需要我们颠倒横轴纵轴来帮助我们简化面积公式。比如下图,求 x = y 2 x=y^2 x=y2 与 y = x − 2 y=x-2 y=x−2 所包围形成的面积
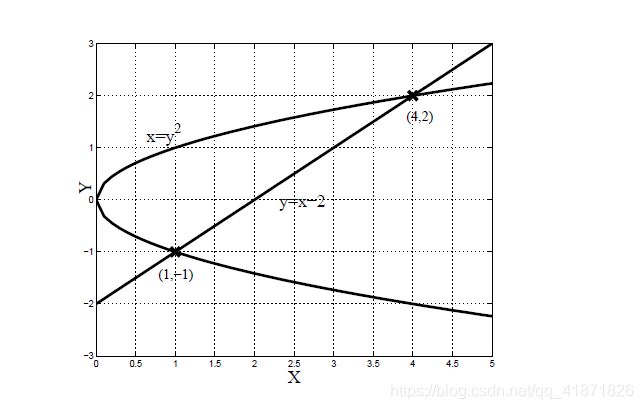
很明显,正常求解过程中,横向的抛物线从正常的角度来看不能被看成函数,而且需要把面积竖直分成两部分,但是交换 X , Y X,\ Y X, Y轴的顺序反而会大大简化运算(把 y y y 看作自变量)。
4.3 求二维曲线轨迹长度(Arc Length)、三维曲面面积和体积(Surface and Volume)
在具体求轨迹长度之前,需要先引入参数方程,因为不同形状的曲线或者是之后多变量微积分中的曲面,根据选取的坐标系的不同,运算量也会不同。比如矩形类或者长方体更适合常用的笛卡尔坐标系( x y z xyz xyz坐标系),而圆柱类,球类则更适合柱坐标系和球坐标系。
4.3.1 坐标系和参数方程(Coordinates and Parametric Equations)
极坐标和笛卡尔坐标系(Polar Coordinates and Cartesian Coordinates)
因为是单变量微积分,坐标系只是二维的。对于那些通过旋转或者依赖角度而生成的曲线来说,把笛卡尔二维坐标系转化为极坐标是非常方便的。
极坐标转化为笛卡尔坐标的公式为:
x = r cos θ x=r\cos \theta x=rcosθ y = r sin θ y=r\sin \theta y=rsinθ
笛卡尔坐标转化为极坐标的公式为:
r = x 2 + y 2 r=\sqrt{x^2+y^2} r=x2+y2 θ = tan − 1 y x \theta=\tan^{-1}\frac{y}{x} θ=tan−1xy
其中 r r r是到坐标原点的距离(一般来说范围是 0 ≤ r ≤ ∞ 0\leq r\leq \infty 0≤r≤∞), θ \theta θ 是点与原点的连线和水平轴所成的角(一般来说范围是 − π ≤ θ ≤ π -\pi\leq\theta\leq\pi −π≤θ≤π 或者 0 ≤ θ ≤ 2 π 0\leq\theta\leq 2\pi 0≤θ≤2π)
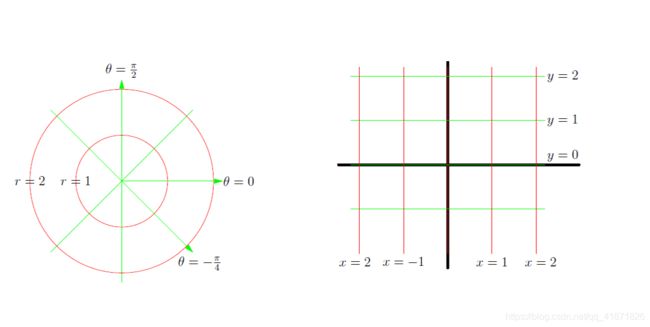
例如,将 y = 1 y=1 y=1转化到极坐标中
y = 1 = r sin θ y=1=r\sin\theta y=1=rsinθ r = 1 sin θ r=\frac{1}{\sin\theta} r=sinθ1
参数方程
参数方程的目的是将原本的两个变量 x , y x,\ y x, y分别表示成另外一个变量(比如说时间 t t t)的函数,这种方式在实际应用中是非常有用的,因为我们可以通过中间变量来获得 x , y x,\ y x, y的关系:
{ x = x ( t ) y = y ( t ) \left\{ \begin{aligned} x&=x(t)\\ y&=y(t) \end{aligned} \right. {xy=x(t)=y(t)
常见的例子就是圆的参数方程
{ x = r cos t y = r sin t \left\{ \begin{aligned}x&=r\cos t\\y&=r\sin t\end{aligned}\right. {xy=rcost=rsint
也就是 x 2 + y 2 = r 2 x^2+y^2=r^2 x2+y2=r2。
4.3.2 弧长对应的微分形式
1. 笛卡尔坐标系下求曲线弧长的微分形式是:
( Δ s ) 2 ≈ ( Δ x ) 2 + ( Δ y ) 2 (\Delta s)^2\approx(\Delta x)^2+(\Delta y)^2 (Δs)2≈(Δx)2+(Δy)2
转化成微分形式:
d s 2 = d x 2 + d y 2 → d s = d x 2 + d y 2 ds^2= dx^2+dy^2\quad\to\quad ds=\sqrt{dx^2+dy^2} ds2=dx2+dy2→ds=dx2+dy2 d s = 1 + d y 2 d x 2 d x = 1 + d y 2 d x 2 d x = 1 + f ′ ( x ) 2 d x ds=\sqrt{1+\frac{dy^2}{dx^2}}\ dx=\sqrt{1+\frac{dy^2}{dx^2}}\ dx=\sqrt{1+f'(x)^2}\ dx ds=1+dx2dy2 dx=1+dx2dy2 dx=1+f′(x)2 dx
2. 极坐标系下求曲线弧长的微分形式是:
d s = r d θ ds=rd\theta ds=rdθ
简单的弧长计算。
3. 参数方程下求曲线弧长的微分形式是:
d s = d x 2 + d y 2 = ( d x 2 d t 2 ) + ( d y 2 d t 2 ) d t ds=\sqrt{dx^2+dy^2}=\sqrt{\Big(\frac{dx^2}{dt^2}\Big)+\Big(\frac{dy^2}{dt^2}\Big)}\ dt ds=dx2+dy2=(dt2dx2)+(dt2dy2) dt
4.3.3 壳层法和圆盘法(Methods of Shells and Disks)——应对旋转类几何问题
普通切割法
普通切割法源于最简单的微分方法,将一个三维物体沿某个方向切成一小片。这种方法适用于竖直堆砌的底面不为圆类的物体
Δ V ≈ A ⋅ Δ x \Delta V\approx A\cdot\Delta x ΔV≈A⋅Δx这里 A A A是每一小片的底面积,也是关于某一变量 x x x的函数, Δ x \Delta x Δx是厚度。上面的式子取极限再积分之后就是
V = ∫ A ( x ) d x V=\int A(x)dx V=∫A(x)dx
壳层法
壳层法求体积
壳层法求体积一般用于曲线绕竖直轴旋转的情况,如下图所示。
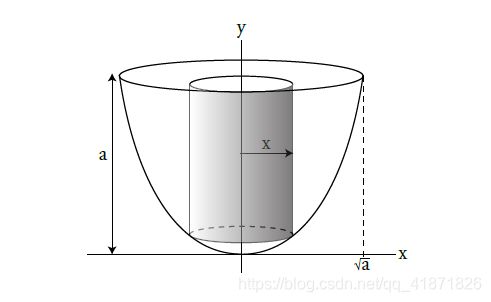
壳层法本质就是叠加每一层壳(通俗理解就是薄薄的一个空心圆柱体),微分的空心圆柱体的体积公式类似于厚度极小的长方体,由侧面积乘厚度得到。
d V = 2 π x f ( x ) ⎵ Side Area ⋅ d x ⎵ Thickness dV=\underbrace{2\pi xf(x)}_{\text{Side Area}}\cdot \underbrace{dx}_{\text{Thickness}} dV=Side Area 2πxf(x)⋅Thickness dx
通过积分可以得到公式:
V = ∫ a b 2 π x f ( x ) ⎵ Side Area ⋅ d x ⎵ Thickness V=\int_a^b\underbrace{2\pi xf(x)}_{\text{Side Area}}\cdot \underbrace{dx}_{\text{Thickness}} V=∫abSide Area 2πxf(x)⋅Thickness dx
(注意!这里的 f ( x ) f(x) f(x)只是表示高度,不一定和曲线的表达式一样,比如上图中的 f ( x ) = a − x 2 f(x)=a-x^2 f(x)=a−x2而不是 f ( x ) = x 2 f(x)=x^2 f(x)=x2)
圆盘法
圆盘法求体积
圆盘法一般用于曲线绕水平轴旋转的情况。如下图,
可以发现旋转后的体积可以通过对 x x x轴某处的一小块圆盘做积分得到。微分形式是:
d V = π f ( x ) 2 ⎵ Base Area ⋅ d x ⎵ t h i c k n e s s dV=\underbrace{\pi f(x)^2}_{\text{Base Area}}\cdot\underbrace{dx}_{thickness} dV=Base Area πf(x)2⋅thickness dx
积分可以得到:
V = ∫ a b π f ( x ) 2 ⎵ Base Area ⋅ d x ⎵ t h i c k n e s s V=\int_a^b\underbrace{\pi f(x)^2}_{\text{Base Area}}\cdot\underbrace{dx}_{thickness} V=∫abBase Area πf(x)2⋅thickness dx
圆盘法求曲面面积(Surface Area)
对于旋转体的曲面面积,可以类比圆柱的侧面面积公式,底面周长与高度的乘积。而对于一般旋转体而言,就是一小段弧长作为圆盘的厚度。
如果物体是绕 y y y轴而成的,面积微元为(用 d s ds ds表示一小段弧长):
d S = 2 π x ⎵ Circumference ⋅ d s ⎵ Height dS=\underbrace{2\pi x}_{\text{Circumference}}\cdot \underbrace{ds}_{\text{Height}} dS=Circumference 2πx⋅Height ds
积分之后就得到:
S = ∫ a b 2 π x ⎵ Circumference ⋅ d s ⎵ Height S=\int_a^b\underbrace{2\pi x}_{\text{Circumference}}\cdot \underbrace{ds}_{\text{Height}} S=∫abCircumference 2πx⋅Height ds
如果物体是绕 x x x轴而成的,面积微元为(用 d s ds ds表示一小段弧长):
d S = 2 π y ⎵ Circumference ⋅ d s ⎵ Height dS=\underbrace{2\pi y}_{\text{Circumference}}\cdot \underbrace{ds}_{\text{Height}} dS=Circumference 2πy⋅Height ds
积分之后就得到:
S = ∫ a b 2 π y ⎵ Circumference ⋅ d s ⎵ Height S=\int_a^b\underbrace{2\pi y}_{\text{Circumference}}\cdot \underbrace{ds}_{\text{Height}} S=∫abCircumference 2πy⋅Height ds
参数方程下的曲面面积
如果变量 x , y x,\ y x, y表示成了参数方程,这时候只需要把弧长公式换成参数方程下的情况即可,其他思路不变。
4.4 求概率(Bell Curve)
(积分应用之概率求解请参考上面的链接。)
4.5 微分方程简介(Differential Equations)
简单举例
大三大四学控制的时候印象最深刻的就是微分方程组了。微分方程如其名,就是把函数的微分引入方程当中,比如说对汽车的控制需要知道加速度,速度,角速度,角加速度的信息,而这些信息都是关于位移或者角度的微分。
本节只是对微分方程的简介,如果以后听了MIT 18.03微分方程这门课后,我也会专门做一下笔记。
经典的一个微分方程的例子是:
( d d x + x ) y = 0 \Big(\frac{d}{dx}+x\Big)y=0 (dxd+x)y=0
其中 ( d d x + x ) \Big(\frac{d}{dx}+x\Big) (dxd+x)被称为湮没算符(annihilation operator)
微分方程的解法核心就是分离变量(Separation of Variables),本例中,打开括号后方程可以写成:
d y d x = − x y → d y y = − x d x \frac{dy}{dx}=-xy\quad\to\quad\frac{dy}{y}=-xdx dxdy=−xy→ydy=−xdx
两边同时积分,
∫ d y y = − ∫ x d x \int \frac{dy}{y}=-\int xdx ∫ydy=−∫xdx ln y = − x 2 2 + C ( assume y > 0 ) \ln y=-\frac{x^2}{2}+C\quad (\text{assume} \ y>0) lny=−2x2+C(assume y>0) y = exp ( − x 2 2 + C ) = e c e − x 2 2 = A e − x 2 2 ( A = e c ) y=\exp(-\frac{x^2}{2}+C)=e^ce^{-\frac{x^2}{2}}=Ae^{-\frac{x^2}{2}}\quad(A=e^c) y=exp(−2x2+C)=ece−2x2=Ae−2x2(A=ec)
结果类似标准正太分布。
分离变量
一般来说,微分方程的形式为:
d y d x = f ( x ) g ( y ) \frac{dy}{dx}=f(x)g(y) dxdy=f(x)g(y)
分离变量之后再积分为:
∫ d y g ( y ) = ∫ f ( x ) d x \int \frac{dy}{g(y)}=\int f(x)dx ∫g(y)dy=∫f(x)dx
令:
H ( y ) = ∫ d y g ( y ) ; F ( x ) = ∫ f ( x ) d x H(y)=\int \frac{dy}{g(y)};\ \ F(x)=\int f(x)dx H(y)=∫g(y)dy; F(x)=∫f(x)dx
H ( y ) = F ( x ) + C H(y)=F(x)+C H(y)=F(x)+C就是微分方程的隐式解(Implicit Solution)